Published
in 2001 Theory & Psychology, 11, 97-117.
Scientific
Models, Connectionist Networks, and Cognitive Science
Christopher
D. Green
Department of
e-mail: christo@yorku.ca
Abstract
The employment of a particular class of computer programs known as "connectionist networks" to model mental processes is a widespread approach to research in cognitive science these days. Little has been written, however, on the precise connection that is thought to hold between such programs and actual in vivo cognitive processes such that the former can be said to "model" the latter in a scientific sense. What is more, this relation can be shown to be problematic. In this paper I give a brief overview of the use of connectionist models in cognitive science, and then explore some of the statements connectionists have made about the nature of the "modeling relation" thought to hold between them and cognitive processes. Finally I show that these accounts are inadequate and that more work is necessary if connectionist networks are to be seriously regarded as scientific models of cognitive processes.
This paper is about the viability of connectionist networks -- a class of computer program with a particular kind architecture -- considered as models of human cognition. After a few general remarks about the historical relation between psychology in general and philosophy of science, I describe developments in the methodology and metatheory of cognitive science from the inception of symbolic computer models of cognition in the 1950s to the advent of connectionist models of cognition in the 1980s. I describe connectionist models in some detail in order to highlight some difficulties discussed in the latter half of the paper. Then I describe and critique the approaches of some key advocates of connectionism with respect to the question of the exact sense in which connectionist simulations of cognitive processes are to be regarded as scientific models. Finally, I examine the application to connectionist cognitive science of one of the most influential recent accounts of scientific explanation -- Nancy Cartwright's "simulacrum" account of explanation. My conclusion is that the relation of connectionism to cognition remains a quite confused one, and that advocates of connectionism will have to make some hard choices about precisely what they are aiming to model if they are to make significant headway.
I
Almost since its inception, the main focus of the philosophy of science has been physics. In recent decades, however, there has been an expansion in the scope of philosophy of science. In particular, the philosophy of biology has come to enjoy a significant, if still secondary, place in the philosophical investigation of scientific practice. In many ways the philosophy of biology has been able to flourish not because of the similarities it is seen to have with physics, but rather because of the differences between the ways in which biology and physics are practiced.
But what of the application of the insights of philosophy of science to psychology? In the "hey day" of behaviorism, there was some discussion of its philosophy, but there were so many different strands of behaviorism, and the differences between what philosophers and psychologists regarded as behaviorism were so strong, that it never really flourished as a distinct area within the discipline of philosophy of science. What is more, the downfall of behaviorism as the dominant approach to psychology in the 1960s and 1970s made its philosophy moot.
In the last few decades, however, a new approach to the study of the mind has risen to prominence, based upon an analogy -- perhaps even an identity -- between the activity of the mind and that of the computer. It has been pursued not only by psychologists but also by philosophers, linguists, computer scientists, and neuroscientists, and generally goes by the name "computational cognitive science" (CCS). The CCS program was presaged in the work of Warren McCulloch and Walter Pitts (1943/1965), as well as in that of Alan Turing (1950), but it first came into full view with the pioneering work of Herbert Simon and Allen Newell in the late-1950s and in the 1960s (Newell & Simon, 1963, 1972). Their program for the scientific study of cognition, most explicitly laid out in their article "Computer science as empirical inquiry" (1976/1981), is that the mind is a "Physical Symbol System" (PSS). As they put it:
A physical symbol system consists of a set of entities, called symbols, which are physical patterns that can occur as components of another type of entity called an expression (or symbol structure). Thus a symbol structure is composed of a number of instances (or tokens) of symbols related in some physical way (such as one token being next to another). At any instant of time the system will contain a collection of these symbol structures. Besides these structures, the system also contains a collection of processes that operate on expressions to produce other expressions: processes of creation, modification, reproduction, and destruction. A physical symbol system is a machine that produces through time an evolving collection of symbol structures. Such a system exists in a world of objects wider than just these symbolic expressions themselves. (p. 40)
Newell and Simon go on to stipulate that such symbolic expressions can be said to "designate" objects apart from themselves just in case they can physically affect them or affect behavior with respect to them, and that the system can "interpret" such expressions if they can carry out the processes they describe.1 Foremost in their minds is that the modern digital computer satisfies their definition of a PSS.
With this background laid out, Newell and Simon then go on to articulate their theory of cognition:
The Physical Symbol System Hypothesis. A physical symbol system has the necessary and sufficient means for general intelligent action. (p. 41)
By inference, then, if a PSS is necessary and sufficient for intelligence, and if the mind is intelligent, then the mind must also be a PSS. The brain is the "hardware" or "computer," and the mind is the "software" or "program".2 One important implication of this conclusion is that the study of the brain is not terribly important to the study of the mind -- just as a particular program can be run on wide variety of computers whose physical makeups need not be very similar, so the same "mind" could be "run" on a wide variety of computers, the brain being but one. To use the terminology of the day, minds are "multiply realizable" on diverse physical systems. They may supervene on brains as a matter of fact, but they are not reducible to brain activity.
Although many have quibbled about the details of the Physical Symbol Systems Hypothesis (PSSH), cognitive science was guided by its general thrust through the 1970s and most of 1980s. Broadly similar proposals were articulated around the same time by Hilary Putnam (1960/1975), Jerry Fodor (1975), and a host of others.
The general plan of research associated with this approach to cognition was to "model" various cognitive processes with symbolic computer programs. The exact meaning of the term "model" here is of particular significance for the present paper because, given the details of this particular research program, the relationship between the model and the thing being modeled is one of instantiation: according to the PSSH cognition just is the manipulation of physical symbols in such-and-such a fashion. If that process is carried out on a computer, the computer has not merely simulated3 a cognitive act in the way that a computer simulates, say, a weather system without producing an actual storm. By contrast, under the PSSH, to carry out a cognitive "simulation" is literally to create a cognitive process.
John Searle developed on this point in his famous article "Minds, Brains, and Programs" (1980). Those who believe that there is an essential difference between the computer model of cognition and the "real thing" -- a difference parallel, say, to that which holds between a computer model of a weather system and a real storm -- espouse only what he called "weak AI" and do not believe the PSSH. As a result, however, they still made no specific claim about what relation holds between the brain and the mind. Those, on the other had who believe there to be no essential difference between the computer model of the cognitive process and in vivo cognitive process are advocates of what he called "strong AI" and are committed to the PSSH (or some similar position).
This is a much stronger sense of the term "model" than is typically used in the physical sciences. Computer models of physical processes are not thought to be literal instantiations of the physical process being modeled. Given the details of PSSH, however, the computer model of cognition must be regarded as creating the very cognitive process being "modeled."
II
By the mid-1980s, however, a number of problems with the symbol-processing view of cognition had come to light. First of all, symbol-processing models tend to be brittle -- they "crash" whenever they have incomplete information or when the processor has suffered even minor damage. By contrast, people seem to be much more cognitively resilient -- they give reasonable answers when faced with incomplete information, and although brain damage hampers their abilities, it does not usually cause their cognitive systems to grind to a complete halt. Attempts were made to address such problems by deploying default "scripts" (Schank & Abelson, 1977) "schemas" (Rumelhart, 1980), "frames" (Minsky, 1975), and the like, but such proposals looked very much like "hacks" -- ad hoc solutions having relatively little psychological plausibility.
Second, symbol-processing systems have a very difficult time learning new cognitive domains from scratch. Typically they must have elaborate "conceptual frameworks" programmed into them in advance. Without this, they are unable to pick out the "regularities" in a new situation, or even make reasonable hypotheses about what the regularities might be. A third problem is that symbol-processing systems have difficulty generalizing their "knowledge" to new, related situations unless these new situations have been specifically envisioned ahead of time by their programmers.
All three of these problems were addressed by a new kind of non-symbolic computational architecture that became popular in the late-1980s. It is variously called "connectionism" or "parallel distributed processing" (PDP). Systems employing such architecture are also sometimes called "neural networks."4 They typically involve dozens, or even hundreds, of simple "units" or "nodes" that are connected together by hundreds, or even thousands, of simple connections that transmit "activation" from one unit to another. The activation level of each unit is determined by some specified mathematical function of the activity transmitted to it from other units via its input connections. The activation the unit transmits to other units is determined by some specified function of its own activation level. A small example follows:
E
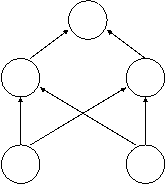 q = 1.0, input = 1.07
q = 1.0, input = 1.07
1
1.5 .8
C .5 .4 D
.5 .4 .3 .2
A 1 0 B
Figure 1. A sample connectionist network.
This network has five units arranged into three layers, with six connections linking them together. The two "input units" (A and B, at the bottom of the network) begin with activation levels of 1 and 0, respectively. The "weight" on the connection from unit A to unit C of the "intermediate" or "hidden" layer (in the middle of the network) is .5.5 That on the connection between units B and C is .3. Let us assume that in this network the activation for the hidden units is given by the sum of weighted activations of the units connected to it from below. Thus, the activation for unit C is given by the activation of unit A multiplied by the weight on the connection between A and C, plus the activation of unit B multiplied by the weight on the connection between B and C: (1)(.5) + (0)(.3) = .5. Similarly, the activation for unit D is (1)(.4) + (0)(.2) = .4. Calculating the activation for the output unit of the network (unit E at the top of the network) is slightly different. Unit E has a threshold (q) associated with it equal to 1.0. This means if the incoming activation is greater than 1.0, the unit "turns on" by assuming an activation level of 1. If the incoming activation does not reach this level, the unit "turns off" by assuming an activation level of 0. In this particular example, the incoming activation is calculated just as it was before: (.5)(1.5)+(.4)(.8) = 1.07. Because this exceeds the threshold value of 1.0, the unit becomes active, assuming an activation level of 1.
What does all this have to do with cognition? This particular example calculated nothing of importance. Its details were simply a way of showing some basic aspects of how such networks functioning. Networks like this one, however, have be built to identify objects,6 pronounce written English words (Rosenberg & Sejnowski, 1987), parse sentences (Berg, 1992), derive deductively valid conclusions from propositional premises (Green, 1992), choose the best evinced scientific theory from among a set of available options (Thagard, 1988), and simulate a wide array of other cognitive processes.
What is more, unlike symbolic systems, connectionist systems are able to learn new domains more or less from scratch. That is, given a very general learning rule,7 a network beginning with connection weights set to random values can become apparently proficient at many kinds of cognitive processes. In addition, once they have learned a given domain, they are fairly resistant to the problems posed by receiving incomplete information, and even to damage to their internal structure (i.e., setting some of the weights to 0 after training). Their performance under such conditions is said to "degrade gracefully" -- they continue to make seemingly reasonable "guesses" at the right answers to the problems with which they are faced. Finally, they are able to generalize their "knowledge" reasonably well to entirely new instances that were not part of the set of material on which they were trained. For instance, a network called LOGINET2 (Green, 1992) was trained to complete 80% of the standard transformations of propositional logic.8 Afterwards, it was able to correctly transform the 20% that had not been used during training without any additional training. All these advantages have made the connectionist modeling of cognitive processes the dominant methodology of cognitive science in the 1990s.
A crucial element of connectionist networks that makes these advantages possible, however, is that the units -- particularly the "intermediate" or "hidden" units -- are not symbolic. In traditional symbolic systems, the "parts" of the system -- the variables and functions -- correspond to identifiably cognitive entities or processes. In particular, the symbolic expressions are thought to model beliefs, desires, or other propositional attitudes that in vivo cognitive systems are assumed to have. In connectionist networks, however, this is not the case, the "mental representations," to the degree that they are admitted to exist at all,9 are said to be "distributed" over the activity of the entire network, not localized in a particular unit or identifiable subset of units (see, e.g., Van Gelder, 1991). For instance, in Newell and Simon's LT -- an influential early AI program that modeled logical deduction -- one could easily point to a part of the program in which, say, the "É" was removed from the expression pÉq, and replaced with a Ú between the variables and a "~" in front of the p. In LOGINET2 (Green, 1992), however, there is no such thing. The interetable (i.e., symbolic) bank of input units encodes the expression pÉq, and another interpretable bank of output units encodes the expression ~pÚq, but the activity of the layer of "hidden" units between these, and the associated connections, simply cannot be characterized in logical, or otherwise symbolic, terms at all (except, of course, in terms of the mathematics of the activation and learning rules). It is non-symbolic. The various "rules" of logical transformation -- inasmuch as they can be said to reside there at all -- are distributed across the whole network in a "superposed form" (Ramsey, Stich, & Garon, 1991). The process that enables the network to transform, say, conditionals into disjunctions is the very same one that enables it to enact, say, the De Morgan transformations (i.e., conjunctions into disjunctions, and vice versa).
A serious question for philosophers of science that is raised by the shift from symbolic to connectionist systems in cognitive science, then, is "What exactly do connectionist models model?" With traditional symbolic models, problematic as they may have been in other ways, the answer to this question was clear: the symbolic expressions model the beliefs, desires, and other propositional attitudes that cognitive systems are assumed to have. The component parts of those expressions, in turn, model the constituent parts of those expressions -- e.g., concepts. Similarly, the rules contained in symbolic programs model the cognitive processes of memory, inference, interpretation, and the like. In connectionist networks, however, none of this is true. Neither the connections nor the units can be said to model concepts or attitudes. They are, strictly speaking, uninterpretable.
So how do we know that we have a cognitive system at all? One might be tempted to say because the system as a whole acts like a cognitive system. But, since we know from traditional philosophy of science that, strictly speaking, infinitely many different theories can perfectly capture any finite set of data, all we can really say is that we have developed a system that captures the data at hand; we have no reason to believe that there is anything particularly "cognitive" about the way in which connectionist systems capture this data.
Consider the following analogy:10 An historian figures out how to encode a set of political and socio-economic variables surrounding a large number of past political uprisings in such a way that they can be input into a connectionist network. The resulting output of the network represents a number of possible political outcomes (e.g., overthrow of the government, suppressed attempt to overthrow the government, sporadic unrest leading substantial political change, etc.). After training the network, it is able to give the historically correct output for each set of inputs (e.g., given the conditions just prior to the French revolution, the network "predicts" the overthrow of the government, etc.). Because all of the internal representations (if indeed there be any) of the network are "distributed," however, it is well-nigh impossible to say exactly why the network works. The "hidden" units do not correspond to anything in the domain of history or political science. They just get the right answers in a wide array of cases. This situation naturally leads us to the question of whether the network, successful as it is, really teaches us anything about the historical processes leading to revolution. It does not embody any particular theory of revolution -- it is just a machine for computing the "right" results. Similarly with cognition: Is a machine that simply generates the "right" cognitive responses to certain kinds of input of any interest to the person who wants to understand how cognition works -- viz., the cognitive scientist?
It is precisely here that the use of a popular phrase for connectionist systems -- "neural networks" -- clouds the issue. It has been suggested by many that the units and connections of connectionist systems are to be regarded as idealizations of neurons. If taken literally, we would have a solution to the problem here under consideration: it could be argued that connectionist systems do not directly model cognition at all, except inasmuch as cognition takes place in the brain. What they model instead is brain activity -- each unit and its associated connections corresponding to a particular neuron (or perhaps a specific group of neurons). In such a case we would no more expect the individual units to represent particular concepts or attitudes than we expect individual neurons to map one-to-one on to these.
III
Connectionist researchers, however, have been notoriously ambivalent about the claim that their units model neural structures, and not without good reason. Despite some superficial similarities, the way in which connectionist networks are constructed appears to violate some basic facts of neural function. These are enumerated and discussed by Crick and Asanuma (1986).11 What is more, to restrict the operation of units in connectionist systems to that known to be true of actual in vivo neurons might well force connectionists to give up some of the most advantageous aspects of these kinds of systems. As a result, we find some of the leading connectionists wary of depending too heavily on the presumed analogy between units and neurons.
McClelland, Rumelhart, and Hinton (1986), for instance, say that connectionist models "seem much more closely tied to the physiology of the brain than other information-processing models" (p. 10), but then they retreat to saying that their "physiological plausibility and neural inspiration ... are not the primary bases of their appeal to us" (p. 11).
Smolensky (1988) has attempted to map this territory more fully. After having examined a number of possible "mappings" between connectionist units and various aspects of the neurological domain, he writes that "given the difficulty of precisely stating the neural counterpart of components of subsymbolic [i.e., connectionist] models, and given the very significant number of misses, even in the very general properties considered..., it seems advisable to keep the question open" (p. 9). Only with this caveat in place does he then go on to claim that "there seems no denying, however, that the subconceptual [i.e., connectionist] level is significantly closer [emphasis added] to the neural level than is the conceptual [i.e., symbolic] level" (p. 9). Precisely what metric he is using to measure the "closeness" of various theoretical approaches to the neural level of description is left relatively unexplicated, however. He says that "the sub-conceptual level does incorporate a number of features of neural computation that are almost certainly important to understanding how the brain computes" (p. 9), but then goes on to say that "on semantic measures, the sub-symbolic level seems to be closer to the conceptual level" (p. 9).
One of the crucial difficulties here is an apparent conflation, not uncommon in the connectionist literature, of two entirely distinct senses of the term "representation." In one sense, every theory represents things, states, processes, etc. of the world. Physical theories may represent, for instance, protons, neutrons and electrons. Consider the Bohr diagram of the atom:
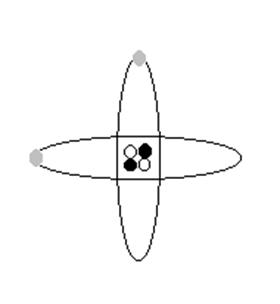
Figure 2. A Bohr model of an atom.
Assume that the white circles represent protons, the black circles neurons, and the grey circles electrons. The ellipses are the electron paths. I will call this kind of representational relation t-representation (for theoretical representation). Note that the objects represented by the physical theory -- the actual atoms, neutrons, and electrons -- do not in turn represent something else; they are not themselves intentional objects.
In theories of cognition, however, there is an additional wrinkle. Just as in physical theories, there will be entities in a given cognitive theory that represent (t-represent) the objects of the cognitive domain -- e.g., beliefs, desires, actions, etc. In addition, however, the objects represented by the theory -- viz., the beliefs, desires, actions, etc. -- are themselves thought to be representational. Beliefs represent the way the cognitive system in question thinks the world is; desires represent the way it wants the world to be; and so forth. This second order of representation is their semantic content; their meaning. I will call this s-representation (for semantic representation). Serious confusion can arise from conflating these two kinds of representation.
THEORETICAL
ENTITIES
![]()
t-representation

s-representation?
![]() REAL
REAL
WORLD
ENTITIES
Figure 3. A diagram of the distinction between t-representation and s-representation.
Smolensky (among others) expends some effort discussing what the semantic content of the units of connectionist networks -- what their s-representation is. Important a question as this is (though I believe it is premature and somewhat confused, as I explain below), it is not the question of this paper. I am asking a logically prior question -- what is their t-representation? What is it in the actual, living cognitive domain that the units of connectionist models of cognition t-represent? The reason the question of what connectionist units s-represent is confused is that theoretical entities do not really s-represent at all; they t-represent. The objects they t-represent -- the actual beliefs, desires, concepts, or subsymbolic "whatevers" -- are the ones capable of s-representing.12 The question is premature because until we know what, if anything, connectionist units t-represent, we cannot be at all sure that these objects s-represent at all. Indeed, if it turns out that they t-represent nothing at all -- i.e., there is nothing at all in the cognitive (or neural) domain that corresponds to connectionist units, then the question of their s-representation cannot even arise. The crucial difficulty with Smolensky's (1988) "proper treatment of connectionism," then, is that he never seriously addresses the question of what connectionist units t-represent. We are told that the units do not t-represent concepts (though they are said to be "semantically close" to them) and we are told that they do not t-represent neurons or neural circuits (though they are said to be "syntactically close" to them), but then the discussion shifts to what they putatively s-represent (section 7).
Under pressure primarily from the criticisms of Jerry Fodor and his colleagues (Fodor & Pylyshyn, 1988; Fodor & McLaughlin, 1990, Fodor, 1991) Smolensky's theoretical position developed significantly over the next decade. Smolensky (1995) argued that the connectionist level of description lays out the causal structure of cognition, but that what he called "core parts of higher cognitive domains" -- most notably language -- are explained by symbolic functions. Smolensky goes to great lengths to show that symbolic level of description can be explanatory without being regarded as causal and, conversely, that the connectionist level can serve as the causal underpinnings of higher cognition without being explanatory. Very roughly, he argues that symbols are "embeded" in distributed connectionist representations (without the latter simply implementing the former, à la Fodor & Pylyshyn's (1988) critique) via his tensor product approach.
I do not believe he fully succeeds in this attempt, but that is not at issue here. More to the present point, he never fully explains what it is that connectionist units t-represent such that these entities could enter into real world causal relations at all. Indeed he displays much the same ambivalence toward the neural level of description as he did in 1988. He openly concedes that "there are truckloads of facts about the nervous system which are ignored by PDP principles," but goes on to assert that "while the principles of neural computation which shape PDP are few, they are absolutely fundamental, and they are ignored entirely by Classical [i.e. symbolic] theory," and thus, he says, it would be "preposterous" for symbolic theorists to criticize connectionists on these grounds (1995, p. 227). Perhaps it would, but from a less partisan vantage point, it seems entirely reasonable to ask of connectionists that, if they believe connectionist networks to model neural activity, they attempt to include whatever is known about real neural activity into the networks to see if they continue to "save the phenomena" as well under these conditions. If they cannot, then we know there is something wrong with the theory (viz., that cognition is just the operation of a connectionist network).
The connectionist is likely to respond with something like, "units and connections were never intended to model neural activity directly, neuron by neuron. It is, of course, true that connectionist networks incorporate some features -- backpropagation of error is a classic example -- that no neuron is known to accomplish, but surely a 'circuit' or 'system' or 'assembly' of neurons could do what the single unit of a connectionist model does." Indeed it could, but what is sauce for the goose is sauce for the gander: if we are going to allow this kind of many-to-one mapping for connectionist models then it is only fair that we allow it for symbolic models as well. Since it is well-known that even a small number of neurons could be arranged such that they can compute classic symbolic functions (consider, e.g., McCulloch & Pitts' (1943/1965) logic networks), this move gets symbolists off the hook just a surely as it does connectionists. We are left right back at the original question -- just exactly what are the theoretical elements of cognitive models supposed to be modeling?
This is precisely where eliminativist connectionism, such as that of Paul Churchland, shows its greatest strength, and weakness. Through the 1980s and most of the 1990s, Churchland (e.g., 1989) favored eliminating the vocabulary of beliefs and desires from scientific psychology in favor of a "neurocomputational" description of cognition. Thus, it is relatively clear what connectionist units t-represent on his account: the activity of neurons or neural circuits of some sort. Nevertheless, even Churchland concedes that the exact relationship between the units of connectionist systems and the neural structure of the brain remains a major hurdle to be overcome if connectionism is to succeed. In particular, he notes that,
real axons have terminal end bulbs that are uniformly inhibitory, or uniformly exictatory, depending on the type of neuron. We seem not to find a mixture of both kinds of connections radiating from the same neuron, nor do we find connections changing their sign during learning, as is the case in the models. Moreover, that mixture of positive and negative influences is essential to successful function in the models... (1990, p. 221, italics added)
This places connectionists in a serious dilemma. If they are unwilling to take as a literal hypothesis the apparent analogy between the structure of connectionist networks and the neural structure of the brain, then what exactly is it that connectionist networks model? The two most obvious domains to be modeled -- conceptual and neural -- have both been rejected. It might be possible for connectionists to claim that the units and connections of networks correspond to the elements of some new ontological "level" that resides somehow "between" the conceptual and the neural "levels," but thus far, no one has articulated a serious proposal of this sort.
If connectionism is to be taken seriously as a theory of cognition, then connectionists would either have to restrict the activities of their networks to those known to be true of neurons (allowing, of course, for some "idealization"), or they would have to propose a new ontology of cognition. One might well respond that connectionist networks should not be regarded as "theories" of cognition, but rather merely as "models." Connectionists, however, have not been able to supply a plausible account of what exactly constitutes a "model" in this context. If the traditional "semantic" view of models is adopted (see, e.g., Suppes, 1960; Van Fraassen, 1987), connectionist models should serve as a "bridge" of some sort between the in vivo cognitive activities being modeled and some abstract theory whose terms of application to concrete worldly instances of cognition are not made explicit in the theory itself. Unfortunately, there is no such abstract theory -- at least no well-articulated one -- to which connectionist networks can bridge.13
Another connectionist, Michael McCloskey (1991), has taken a quite different approach to explaining the kind of relationship that holds between connectionist models and cognition. He has suggested that connectionist networks are "models" in the same sense that animals are used as "models" of human behavior: one conducts works on animals (often because it would be impractical or unethical to conduct it on humans), and then generalizes the results to the human case. Similarly, according to McCloskey, we can conduct studies on connectionist networks that we find difficult or impossible to perform on humans and then generalize the results to the case of human cognition. In addition to having the freedom to experiment on the networks in whatever ways we might like, because we know the exact structure of the connectionist network at the outset we can presumably learn things we could never learn if we were to experiment on humans (because we can never know the structure of their "neural networks" with equal precision). There is a serious problem with this argument, however. When one experiments on, say, rats in order to obtain answers to questions about humans, one assumes that there is an essential similarity between the rats and the humans -- e.g., that the same laws of conditioning hold for both cases. This assumption is justified by the wide array of similarities in the physiologies and evolutionary histories of the two species (rats and human). Without this justification, the assumption would fail and there would be no basis for generalizing from one to the other. In the case of connectionist networks, there is no reason to assume that they share any relevant similarities with humans at the outset. In fact, strictly speaking, the networks are not even really entities that lend themselves to truly empirical research. They are, instead, formal systems (which is why, incidentally, their structures are exactly known, unlike that of humans). Although it is true that one often runs connectionist programs and then "looks" to see what will happen, these results are just as analytic as are the results of a mathematical derivation; indeed they are just a mathematical derivation. It is not logically possible that they could have turned out other than they did. The fact that one uses a posteriori means (i.e., "looking" at the computed results) to find out what they are does not make them any more empirical14 than asking a mathematician to solve a mathematical problem and then "looking" at her answer after she finishes makes her result empirical (see Kukla, 1989).
IV
Perhaps matters can be elucidated by looking to the philosophy of science literature on the nature and function of scientific models more generally. One of the most influential recent accounts of the operation of scientific models is that presented by Nancy Cartwright's in How the Laws of Physics Lie (1983). In addition to being widely discussed, it has been invoked by a defender of connectionism (Opie, 1998) against arguments of the kind I have made in this paper. Specifically, Opie writes:
What we see here [in connectionism] is the significance of idealisation in science. Idealisation occurs when some of the properties we ascribe to objects in a theoretical model are not genuine features of the objects modelled, but are introduced merely to "bring the objects modelled into the range of the mathematical theory" (Cartwright 1983, p. 153). These properties are often limiting cases of real properties (e.g., frictionless surfaces, perfectly spherical planets), but sometimes they are pure fictions. The point to emphasise is that engaging in idealisation is not equivalent to adopting an instrumentalist attitude towards one's model. A certain amount of idealisation is consistent with a generally realist [emphasis added] attitude towards a model, because there will typically be properties of the objects in the model that are intended as genuine features of the situation being modelled. (Opie, 1998, para. 5)
There are several notable aspects to this passage. First, I do not think that Cartwright would accept Opie's "generally realist" reading of her position (see also McMullin, 1983; Morrison, in press). More important, it is not at all clear how one can remain "generally realist" and accept (without at least some reservation) that some idealizations are "pure fictions." If one is a realist -- i.e., believes that one's model describes some aspect of reality (at least "in the limit") -- and one also believes that important parts of one's model are "pure fiction" -- i.e., are false -- then it would seem that one would be committed to expunging those fictions (in the long run, at the very least). Perhaps, however, there is something in Cartwright's position to help explicate how connectionist networks function as models of cognitive processes. The balance of this paper is dedicated to an exploration of this possibility.
Cartwright discusses the use of models in physics fairly extensively her "simulacrum account of explanation" (1983, chap. 8). In Section 1,15 she distinguishes between two uses of the term "realistic" in physics. One has to do with the relationship between a given model and the physical domain to which it is supposed to correspond. She says, "The model is realistic if it presents an accurate picture of the situation modelled: it describes the real constituents of the system -- the substances and fields that make it up -- and ascribes to them characteristics and relations that actually obtain" (p. 149). Her second kind of realistic model is one in which each factor in the theoretical (typically mathematical) principle being modeled is handled in a plausible way by the model, as opposed to being "black-boxed" in order to make things "come out right." Cartwright writes of this kind of realism: "A fundamental theory must supply a criterion for what is to count as explanatory. Relative to that criterion the model is realistic if it explains the mathematical representation" (p. 150). Cartwright's example can serve to clarify this somewhat. She refers to the block diagram that serves as Louisell's (1973) model of the activity of a laser (see p. 146 of Cartwright, 1983). It is known that the walls of the laser's housing will damp the laser, but Louisell's model makes no mention of that; it contains rather a box labeled "damping." Lousiell's basic equation for lasing also contains a term to account for damping, but the "damping box" in the diagram is not a plausible way of realizing it in the model. It "gets the job done" by including some sort of representation of the damping, but it is not "realistic" in the second of Cartwright's two ways of interpreting the term.16 As Cartwright herself puts it "The reservoir terms…. give rise to the right solutions, but no concrete mechanisms are supplied in the model to explain them"(p. 150).
Let us see if connectionist models of cognition are "realistic" in either of these senses. First, do they "describe the real constituents of the system?" One cannot tell because one does not know which constituents they are supposed to describe. As explained above, connectionists deny that they describe the activity of propositional attitudes or their supposed constituents, and most connectionists are ambivalent about mapping them directly on to the neural structures of the brain. Therefore the answer would seem to be that they are not realistic in the Cartwright's first sense. Are they "realistic," then, in the second sense? Again, one cannot really tell because it is not at all clear what, if anything, the "fundamental mathematical principle" of connectionist cognitive science is. As a result, one cannot tell if "concrete mechanisms are supplied in the model to explain them" or not.
Cartwright offers, however, what she characterizes as an "anti-realistic" alternative -- the "simulacrum account" of explanation:
A model is a work of fiction. Some properties ascribed to objects in the model will be genuine properties of the objects modelled, but others will be merely properties of convenience…. Some of the properties and relations in a model will be real properties in the sense that other objects in other situations might genuinely have them. But they are introduced into this model as a convenience, to bring the objects modelled into the range of the mathematical theory…. It would be a mistake to think [of these] entirely in terms of idealizations -- of properties which we can conceive as limiting cases, to which we can approach closer and closer in reality. For some properties are not even approached in reality. They are pure fictions. (p. 153)
We can now see the context in which Cartwright wrote the passage cited by Opie. So, does Cartwright's anti-realist simulacrum model salvage the hopes of the connectionist? I am inclined to think not. To be sure, she wants to leave plenty of room for the presence of "unreal" terms and entities in scientific models. Her examples include probability distributions in classical statistical mechanics and the medium that Maxwell assumed when modeling the activity of the radiometer. By the same token, however, she seems adamant that at least some of the properties of the model will be "real" as well. If not, how could one even tell whether or not a particular model actually models of the thing being modeled?
On the other hand, Cartwright (1981/1991) is a realist about causal relations, and many connectionists have argued that it is precisely causal relations into which connectionist models give insight. As discussed above in connection with Smolensky's position, however, it is hard to see how connectionists can profess to be realists about causes unless they explicitly connect the constituents of connectionist networks to some particular aspect of the physical world (such as neurons) that can enter into causal relations.
Cartwright's position on scientific models and explanation has, of course, been the subject of continuing controversy (e.g., McMullin, 1983; Morrison, in press), and my invocation of it here should not regarded as a general endorsement of it. The main point of doing so has been, rather, to show that the problems I have identified with connectionist cognitive science are not the product of my having adopted an overly restrictive view of models in science, they are not resolved by the adoption of a more radical point of view. They are, instead, the product of connectionists' own failure to "come clean" on precisely what it is they are modeling.
I began this paper by describing the development of computational cognitive science from the time when symbolic models were the "only game in town" through to when connectionist models rose to prominence because they seemed to offer solutions to a set of important, inter-related problems that haunted the symbolic approach. By (perhaps doggedly) asking the question, "What exactly do connectionist models model?", however, I have tried to show that their apparent success may not come of their being better models, per se, but rather of their advocates being vague about the answer to this question. Just because two things share some properties in common does not mean that one models the other. Indeed, if it did, it would mean that everything models everything else. There must be at least a plausible claim of some similarity in the ways in which such properties are realized in the model and the thing being modeled. Although connectionists do sometimes make the claim that connectionist networks are "like" the neural structure of the brain, they do not hold to it strongly or consistently enough to allow for a rigorous assessment of their position. Connectionist networks either model brain activity or they do not. If they are "idealized" models of neuron, that is fine, as long as connectionists realize that ultimately it is incumbent upon them to "add back" the properties that have been idealized away. If some of the properties are "pure fictions," à la Cartwright, that is fine as well, but even according to her, there should be some properties that map on to aspects of the domain being modeled. Until that mapping is specified, connectionist cognitive scientists' claims to model cognition is as weak as the claim of the fictional connectionist historian to be modeling historical processes, and the proper interpretation of their results will remain equally obscure.
References
Berg,
G. (1992). A connectionist parser with recursive sentence
structures and lexical disambiguation.
In AAAI-92: Proceedings of the Tenth national conference on
artificial intelligence.
Cartwright,
N. (1981). The reality
of causes in a world of instrumental laws. PSA 1980
(vol. 2), ed. by P. Asquith and R. Giere. Philosophy of Science Association. (Reprinted in R. Boyd, P.
Gasper and J.D. Trout (Ed.),
The philosophy of science.
Cartwright,
N. (1983) How the laws of physics lie.
Chrisley, R. L.
(1995). Taking embodiment seriously: Nonconceptual
content and robotics. In K. M. Ford, C. Glymour,
& P. J. Hayes (Eds.), Android epistemology (pp. 141-166).
Churchland, P. M. (1981). Eliminative materialism and propositional attitudes. Journal of Philosophy, 78, 67-90.
Churchland, P. M.
(1988). Matter and consciousness
(rev. ed.).
Churchland, P. M.
(1989). A neurocomputational
perspective: The nature of mind and the structure of science.
Churchland, P. M.
(1990). Cognitive
activity in artificial neural networks. In D. N. Osherson & E. E. Smith (Eds.), Thinking: An
invitation to cognitive science (Vol. 3, pp. 199-227).
Clark,
A. (1993). Associative engines:
Connectionism, concepts, and representational change.
Collins, A.M. and Quillian, M.R. (1969). Retrieval time from semantic memory. Journal of Verbal Learning & Verbal Behavior, 8, 240-247.
Crick, F.H.C. and Asanuma, C. (1986). Certain aspects of the anatomy and physiology of
the cerebral cortex. In J. L.McClelland &
D. E. Rumelhart Parallel distributed processing:
Explorations in the microstructure of cognition (vol. 2, pp. 333-371),
Cussins, A.
(1990). The connectionist construction of concepts. In
M. A. Boden (Ed.), The
philosophy of artificial intelligence (pp. 368-440).Oxford:
Cussins, A. (1993). Nonconceptual content and the elimination of misconceived composites. Mind and Language, 8, 234-252.
Evans,
G. (1982). The varieties of reference.
Fodor,
J. A. (1975). The
language of thought.
Fodor,
J. A. (1991). Replies. In B. Lower & G. Rey (Eds.), Meaning in mind: Fodor and his critics
(pp. 255-319).
Fodor J. A. & McLaughlin, B. (1990). Connectionism and the
problem of systematicity: Why Smolenky's solution
doesn't work. Cognition, 28,
183-204.
Fodor, J. A. & Pylyshyn, Z. W. (1988). Connectionism and cognitive architecture: A critical analysis. Cognition, 28, 3-71.
Green,
C. D. (1992). Reasoning
and the connectionist modelling of deduction. Unpublished Ph.D.
Dissertation.
Green, C. D. (1998). Are connectionist models theories of cognition? Psycoloquy, 9 (4). URL: ftp://ftp.princeton.edu/pub/harnad/ Psycoloquy/1998.volume.9/psyc.98.9.04.connectionist-explanation.1.green.
Kripke, S. A.
(1972). Naming and necessity.
Kukla, A. (1989). Is AI an empirical science? Analysis, 49, 56-60.
Louisell, W. H.
(1973). Quantum statistical properties of radiation.
McClelland, J. L., Rumelhart, D. E., and Hinton, G. E. (1986). The appeal of parallel distributed processing. In Parallel distributed processing: Explorations in the microstructure of cognition (vol. 1, pp. 3-44), ed. by Rumelhart, D. E. & McClelland, J. L. Cambridge, MA: MIT Press.
McCloskey, M. (1991). Networks and theories: The place of connectionism in cognitive science. Psychological Science, 2, 387-395.
McCulloch, W. S. & Pitts, W. H. (1965). A logical
calculus of the ideas immanent in nervous activity. Reprinted in Warren S.
McCulloch (Ed.) Embodiments of mind (pp. 19-39).
McMullin, E. (1983). Galilean idealization. Studies in the History and Philosophy of Science, 16, 247-273.
Minsky, M. (1975). A framework for representing knowledge. In P. H. Winston (Ed.), The psychology of computer vision (pp. 211-277). McGraw-Hill.
Morrison,
M. (in press). Models and idealisations: Implications for physical theory. In N. Cartwright & M. Jones Idealisations
in physics.
Newell, A. & Simon, H. A. (1963). GPS, a program that simulates human thought. In E. A. Feigenbaum & J. Feldman (Eds.), Computers and thought, E (pp. 279-293). McGraw-Hill.
Newell, A. & Simon, H. A. (1972) Human problem solving. Prentice-Hall.
Newell, A. & Simon, H. A. (1981). Computer science as
empirical inquiry: Symbols and search. Reprinted in J. Haugeland (Ed.), Mind design, (pp. 35-66).
Opie, J. (1998). Connectionist modelling strategies: Commentary on Green on connectionist-explanation. Psycoloquy, 9 (4). URL: ftp://ftp.princeton.edu/pub/harnad/Psycoloquy/1998.volume.9/ psyc.98.9.30.connectionist-explanation.27.opie.
Page, M. (2000). Connectionist modelling in psychology: A localist manifesto. Behavioral and Brain Sciences, 23, 443-467.
Peacocke, C.
(1986). Thoughts: An essay on content.
Putnam,
H. (1975). Minds and
machines. In Mind, language
and reality: Philosophical papers (Volume 2, pp. 362-385).
Ramsey, W., Stich, S.
P., & Garon, J. (1991). Connectionism, eliminativism, and the future of
folk psychology. In W. Ramsey, S. P. Stich,
& D. E. Rumelhart (Eds.), Philosophy and
connectionist theory, ed. by, (pp. 199-228).
Rosenberg, C.R. & Sejnowski,
T.J. (1987).
Parallel networks that learn to pronounce English text. Complex Systems, 1, 145-168.
Rumelhart, D. E. (1980). Schemata: the building blocks of cognition. In Theoretical issues in reading comprehension (pp. 33-58), ed by R. J. Spiro, B. C. Bruce, and W. F. Brewer. Erlbaum, pp.
Schank, R. C. & R. P. Abelson
(1977). Scripts, plans, goals and understanding.
Searle, J. R. (1980). Minds, brains, and programs. Behavioral and Brain Sciences, 3, 450-456.
Smolensky, P. (1988). On the proper treatment of connectionism. Behavioral and Brain Sciences 11, 1-73.
Smolensky, P. (1995). Constituent structure and explanation in an integrated
connectionist/symbolic cognitive architecture. In C. MacDonald & G. MacDonald (Eds.), Connectionism
(pp. 223-290).
Stich, S. (1983). From folk psychology to cognitive science:
The case against belief.
Suppes, P. (1960).
A comparison of the meaning and uses of models in mathematics
and the empirical sciences. Synthese, 24 ,287-300.
Thagard, P.
(1988). Computational philosophy of science.
Turing, A. (1950). Computing machinery and intelligence. Mind, 49, 433-460.
Van Fraassen,
B. (1987). The semantic view of theories. In N. J. Nersessian (Ed.), The
process of science (pp. 105-124).
Van Gelder, T. (1991). What is
the "D" in "PDP"? A survey of the concept
of distribution. In W. Ramsey, S.
P. Stich, & D. E. Rumelhart
(Eds.), Philosophy and connectionist theory, ed. by, (pp. 33-59).
Footnotes
1. Clearly there are
difficulties here. It is not my present
aim, however, to develop a critical analysis of Newell and Simon's
approach. It has been taken to task by
many others. Rather, I will take the
PSSH, broadly conceived,
more or less at face value.
2. During the 1970s, there
was a shift in emphasis from the word "intelligence" to the word
"cognition." I use them
relatively interchangeably here. I also
use the term "mind," and I do so only in its cognitive sense. I make
no claims whatever about, for instance, the emotional or affective aspects of
the mind, or about any particular states of consciousness.
3. This is a word commonly
used in cognitive science, but as we see here, under the PSSH, it is a
misleading term if it leads one to believe that there is some essential
difference between the simulation and the thing simulated. Under PSSH the "simulation" is, in
fact, a full instantiation.
4. These terms are not
exactly synonymous, though they are often employed as though they were. Connectionist networks need not be
non-symbolic. The logic networks of
McCulloch and Pitts (1943/1965) were symbolic, as were the semantic networks of
Collins and Quillian (1969), but symbolic
connectionist networks of these sorts do not have the advantages of the
non-symbolic or "distributed" networks being discussed here (but see
Page, forthcoming). More properly,
non-symbolic systems should be called parallel distributed processing (or PDP)
networks, but this is a cumbersome locution that does lend itself easily to an
adjectival form. The phrase "neural
networks" is quite popular as well, but it implies a solution to one of
the very problems I discuss in this paper -- viz., that the units and
connections of such a network model the neurons of the brain, a claim that is
quite controversial in the connectionist literature and which is discussed below.
5. It is unimportant for the
moment where the values of the connection weights come from. Normally they would take on particular values
as the result of a training process of some sort. Here, however, they are simply given.
6. A particularly
interesting one described by Paul Churchland (1988,
pp. 157-162; 1990) uses sonar profiles to distinguish between underwater rocks
and explosive mines.
7. Space does not permit me
to detail such rules here, but they often amount to something like "if the
activation level of a given output unit is higher than it should be, decrease
by a little bit (mathematically defined) the weights on all the connections
feeding into it, and if it is lower than it should be, increase them all a
little bit." In other kinds of
networks, the aim is simply for the system to replicate the input (across a
large number of different input patterns), or to optimize some function of the
network's overall activity. In such
systems there is no need for an external "supervisor" telling the
system what is a right or wrong answer.
Such systems are therefore characterized as being
"unsupervised." For some
standard introductory articles on connectionism see McClelland, Rumelhart, and Hinton (1986), Smolensky
(1988), or Churchland (1990). For a classic critique, see Fodor and Pylyshyn (1988).
8. i.e., pÉq Û ~pÚq; p&q Û ~(~pÚ~q); etc.
9. Some connectionists (Churchland, 1981; Stich 1983)
have advocated outright "eliminativism" with respect to propositional
attitudes, or other mental properties or entities.
10. This example is adapted
from Green (1998). See, in particular, para. 14-18
for a more detailed account of this "thought experiment."
11. Most important among
these is the fact that no mammalian neuron is known to transmit both excitatory
and inhibitory signals to other neurons, but it is virtually required of
connectionist units that they do this (along connections to different
units). If they are constructed such
that they are unable to do this, the networks typically do not learn and
generalize properly.
12. The theoretical entities
of cognitive theories may model the s-representations of the real-world
entities that they t-represent, but this is not the same a
s-representing themselves. The only situation in which theoretical entities s-represent
themselves would be when the cognitive model itself actually instantiates
real cognition. This is the claim
of what Searle calls "strong AI," but surely it is too strong to be
taken seriously. Does anyone really
believe that the connectionist net they program on their desktop computer has
real cognitive powers? If so, then wouldn't it be some sort of crime to turn it
off?
13. An anonymous reviewer of
an earlier draft of this paper suggested that I should look to the literature
that attempts to combine connectionism with "embodied" non-conceptual
content (e.g., Chrisley, 1995; Clark, 1993; Cussins, 1990, 1993), but I find that this work is not
strictly relevant to the point at issue here.
If we knew what the units of connectionist models were supposed to
t-represented in the cognitive (or neural, or whatever) domain, then we might
conclude that those entities, whatever they might be, s-represent
non-conceptual content -- e.g., embodied "orientings"
toward sounds or other events (Evans, 1982; Peacocke,
1986), experienced indexical understandings (e.g. that color, over there),
etc.. Until we can answer the question of what objects connectionist units t-represent, however, the question of what those
objects s-represent is premature. One
might try to claim that non-conceptual content just is what is
t-represented by units, but I think this attempt would immediately fail. To begin with, there is no sense I can make
of the entailment of this claim that such non-conceptual contents are
"connected together" in a manner similar to the units of
connectionist networks are: transmitting positive and negative "activation"
to each other, etc. Second, one would
then be left with the question of what the non-conceptual contents themselves
s-represent if they are very things t-represented by connectionist units. Could they be both the things t-represented
by the units and s-representations of themselves? I don't even know how to make
sense of such as question. Even to
suggest such as possibility sounds very much as if we have already traveled
well down the road of shoring up a failing position with ad hoc
maneuvers. What I think is really going
on is that Cussins and many other connectionists have
tacitly come to assume that "units" are actual parts of the cognitive
domain without specifying where exactly they reside (e.g., in one's head, in
one's thought patterns, or where ever).
This would be an appropriate
moment to point out that my use of "t-representation" and
"s-representation" has no obvious connection to Cussins'
terms "s-domain" and "t-domain." The similarity is completely coincidental.
14. Because of the
widespread rejection the Kantian "synthetic a priori" in this
century, a certain ambiguity has crept into the term "empirical."
People often use it casually to refer to anything discovered through
observation (e.g., Kripke, 1972). By contrast, I am using it here in its strict
form, meaning only a synthetic (or contingent) truth that is learned a
posteriori (i.e, through observation). Analytic a posteriori claims -- such as
"looking" at the output of a computer program -- are not empirical under this
definition.
15. In my copy of the
chapter, this section, entitled "Bridge principles and 'realistic'
models," is labeled "2" but it comes after Section 0 ("Introduction")
and before another Section 2 ("The simulacrum account of
explanation"), so I assume it is intended to be Section 1.
16. Nor is it realistic in
the first way, but that is not at issue here.
Biographical
Note: Christopher Green is an Associate Professor
in the History and Theory of Psychology program at