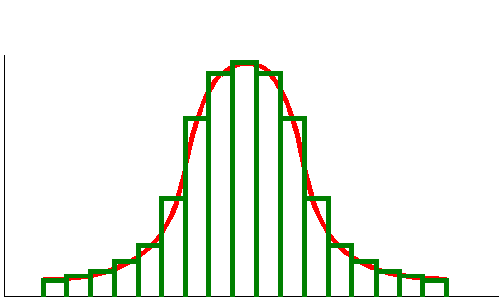
Those who have not studied calculus may find the concept of integration a bit strange. In principle it is really quite easy. Integration is used to find the area enclosed by a curve, the length of a curve or the volume enclosed by a surface.The area of a rectangle is found by multiplying its length by its width. The area under the above curve can be approximated with a series of rectangles. The area of each rectangle is easily determined and the one adds up the areas of all the rectangles to obtain an approximation of the area under the curve. As the number of rectangles under the curve increases the measurement accuracy increases.
When using calculus the actual computations are different, but the principle is the same.
Table of Contents
Subject Index
Table of Contents [When not using frames]