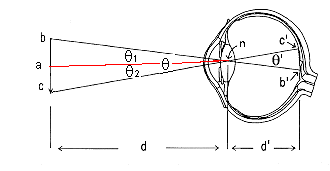
 Figure 1: Visual angles for an object on the horizon. |
Draw the principle rays from the ends of the inverted arrow bc through the nodal point n and extend these principle rays to the retina. Two similar triangles are formed. The first Dbcn has exactly the same angles as Db'c'n. The visual angle of the image on the retina can be calculated by measuring the angle subtended by the object outside of the eye. This is true because q = q'.
Angle q is contained in Dbcn . However, in trigonometry it is convenient to work with right angles. So let's bisect line bc, placing a at its midpoint. q1 is contained in Dban and q2 is contained in Dacn. So, q1 = q2, q = q1 + q2, hence q = 2 x q1 .
q is calculated by dividing line
bc in half and drawing the
red line to n, thus forming a right triangle (Dban). In
other words, distance |ba| = |ac|. The length of the red
line is d. Then q1
is calculated by dividing distance
|ba| by distance d to get tan(q1), and then taking the
arctangent to get angle q1and
finally
q = 2
x q1. These calculations can be easily performed
with a calculator that has trigonometric functions.
| tan(q1) = (|ba| ÷ d) | (1) | ||
| q1 = arctan(|ba| ÷ d) | (2) | ||
| q = 2 x arctan(|ba| ÷ d) | (3) |
If you want to know the distance between bc given that
q is a
given angle, take the tangent of q1and multiply it by the
distance d. This calculation gives you the distance from a
to b To determine the distance between b and
c, multiply the
calculated distance from a to b by 2 and you know the distance
bc.
| |ba| = tan( q1) x d | (4) | ||
| |ba| = tan(q ÷2) x d | (5) | ||
| |bc| = 2 x |ba| | (6) | ||
| |bc| = 2 x (tan(q ÷ 2) x d) | (7) |
Thanks to Dr. Darren Weber for tidying the trigonometric notation