U n i v e r s i t é Y O R K U n i v e r s i t y
ATKINSON FACULTY OF LIBERAL AND PROFESSIONAL STUDIES
SCHOOL OF ANALYTIC STUDIES & INFORMATION TECHNOLOGY
S C I E N C E A N D T E C H N O L O G Y S T U D I E S
NATS 1800 6.0 SCIENCE AND EVERYDAY PHENOMENA
ATKINSON FACULTY OF LIBERAL AND PROFESSIONAL STUDIES
SCHOOL OF ANALYTIC STUDIES & INFORMATION TECHNOLOGY
S C I E N C E A N D T E C H N O L O G Y S T U D I E S
NATS 1800 6.0 SCIENCE AND EVERYDAY PHENOMENA
Lecture 7: It's a Small World
| Prev | Next | Search | Syllabus | Selected References | Home |
Topics
-
It would seem it all started with Stanley Milgram's article The Small World Problem in the very first issue of Psychology Today (1, pp. 60-67, 1967).
The text of this article is not available on the internet. Go to the library. A short commentary by J Kleinfeld on Milgram's article appeared in the Mar/Apr 2002
issue of the magazine:
 Six Degrees of Separation: Urban Myth?
Here is a brief summary from Buchanan's Nexus (p 25-7):
Six Degrees of Separation: Urban Myth?
Here is a brief summary from Buchanan's Nexus (p 25-7):
"Stanley Milgram began his famous small-world experiments [ … ] at Harvard University in the mid-1960's [ … ] A few years before, Milgram had invented what he called the 'lost-letter technique,' a method for probing the attitudes of people within a particular community while avoiding the typical problems of social influence and political correctness that often cloud the results of interviews and questionnaires. As a demonstration, he and some graduate students prepared four sets of one-hundred letters addressed to Friends of the Nazi Party, Friends of the Communist Party, Medical Research Associates, and a private individual named Mr Walter Carnap. They then 'lost' these letters in places where random people would find them. After a few weeks they discovered that while about 70 percent of the letters to Medical Research Associates and Walter Carnap had been returned, only about 26 percent of the others made it. For probing community attitudes on sensitive issues, this lost-letter technique soon came to be used widely in social psychology. [ … ] The small-world experiments were a slight modification of the same method—except that here the point was to learn not about people's attitudes, but about the structure of the social network tying them together [ … ] Strikingly , almost all of the letters arrived in just six steps, indicating that the social world really is immeasurably smaller than we would expect [ … ] As it turns out, the results were not quite as definitive as they might appear. Many letters in the experiments simply never got to Milgram's friend, presumably because they were thrown in the trash bin by some apathetic person along the way. Consequenlty, the letters that did arrive in Boston probably created a biased picture."
In subsequent years, Milgram and others repeated and refined the experiment, and the conclusion seemed indeed to support the surprising fact that "most letters made it to their destination in about six steps." The internet, including the possibility of assembling and accessing large databases, later made this kind of experiment even easier to carry out. For instance, you can participate in one such experiment, by going to the Small World Research Project at Columbia University. "The Small World project is an online experiment to test the idea that any two people in the world can be connected via 'six degrees of separation." Another test you can try requires you to visit The Oracle of Bacon at Virginia, where you can see how many degrees of separation separate actor Kevin Bacon from any other actor, where the criterion is simply the two actors are directly linked if they appeared in the same film. More background on the 'oracle' can be found in Kevin Bacon, the Small-World, and Why It All Matters. A similar, but much more interesting site is The Amazing Baconizer, where, using a database of some 562,729 items (as of November 2003) from the Amazon catalog, the engine tries to connect, with a few hops, any two titles of your choice. Here is the author's description: "At amazon.com, for every musician and author who sells enough product to rise above some water line, they give the five other musicians or authors most closely associated with the artist in question. If you start with Jimi Hendrix, you'll find that people who bought Hendrix's CDs were more likely to also buy CDs by the Stones, the Doors, Led Zep, Stevie Ray Vaughn, and someone I forget. Despite what you may hear at your local schoolyard, buyers of Britney Spears also like Christine Aguilera and the Spice Girls. And so on." Other useful references are, for example, the news item E-mail Study Corroborates Six Degrees of Separation in the August 08, 2003 issue of Scientific American, On Average, How Many Degrees Apart Is Any One Person in the World from Another?, in the November 1, 2003 issue also of Scientific American. See also How Does 'Six Degrees of Separation' Work? Explanation is Personal Networking …. An interesting discussion can be found in Kuro5hin online magazine: Six degrees of separation or unification? (Internet). -
These experiments show that the human world is apparently highly connected. The question is how? why?.
The answers to such questions are still coming in, A good summary can be found in Utopia Theory,
on the Physics Web. The Physics Web? What has physics to do with social psychology or anthropology?
This is an important question, which goes well beyond the issue of six degrees of separation.
Traditionally there has been a sharp separation between the so-called 'hard' and 'soft'
sciences, despite repeated attempts to reduce the latter to the former (positivism, in its strongest,
reductionist form, claimed that the only valid form of knowledge is that of science, and that it is possible,
in principle at least, to reduce all knowledge to physics and, ultimately, to mathematics). The fact is that, except perhaps
for orthodox economics, which however has not been particularly successful, the social sciences have developed
rather independently of the hard sciences.
To recount and understand the history of this apparent rapprochement lies outside the scope of this
course. I will only summarize in a couple of sentences what I believe is the main conclusion. The hard sciences
(i.e. physics, biology and chemistry) until about the end of the 19th century concerned themselves with a
greatly simplified image of the world. This was probably unavoidable, since the actual, real world appears
to be extremely complicated. Consider, for instance, the situation illustrated in the image below. The state
of the balanced broom is rather precarious: any movement of the hand or of the body which displaces the broom
by any angle, no matter how small, from its vertical position leads to the precipitous fall of the broom.
On the other hand, if you hold the end of the handle between your fingers, letting the broom dangle, the equilibrium
is stable, in the sense that, following any relatively small departure from the vertical, the room returns to its vertical,
stable position.

An Example of Unstable Equilibrium
Motion around stable equilibrium is rather easy to describe mathematically. Not so for unstable equilibrium. This is only a trivial example, but it illustrates the sense in which I said that, until recently, the hard sciences concerned themselves with a greatly simplified picture of the world. Of course the social sciences can not really content themselves with an overly simplified picture of man, his behavior and his interactions. Characteristically, man, and life in general, is too varied and unpredictable. Any theory of society which assumes people can be just like the atoms in a gas, is bound to be utterly unrealistic, and therefore useless. This is the basic belief that Milgram and a host of other people gradually undermined, in the sense that they discovered that there are some social, and generally collective, behaviors which can be understood precisely by imagining that, in certain situations, people (or fireflies or swallows or sardines) do behave like interacting atoms. Please, note the qualifiers: social science has not been reduced to physics! See also the last topic below. -
In order to get a more concrete sense of the way these social networks function, let's represent people as dots,
and let's draw a line connecting two given dots to indicate that the corresponding two people know each other.
We can use different colors to differentiate the 'strength' or 'importance' of each link.
 Four Examples of Networks (from Owen Densmore)
Four Examples of Networks (from Owen Densmore)
As you can see from the examples above, there are many ways to draw a network. We can reflect our ignorance about the details by introducing a variable number of random connections. Or we can try to cover all the possibilities by connecting each dot with every other dot. The important point is that, even at a simple glance, there seem to be different types of networks, which may give quite different answers to two questions: a) what is the average number of the smallest number of links connecting an arbitrary dot to another, also arbitrary, dot? (the characteristic path length; b) what is the average probability that two dots, each linked to a third, are also linked? (the clustering coefficient). This is indeed the case, although there is no room here even for a cursory account of the methods used for obtaining the answers. Here I will simply state a few, suprising, results. For further details you are invited to read Buchanan's Nexus.. One of the paradoxical results is that, as far as the number of degrees of separation is concerned, strong social links don't really play an important role. It is the weak links that count. This is how Buchanan puts it (p. 41-4):"If two of my friends have things in common with me, they will also tend to have things in common with each other [ … ] if one person is strongly linked to two others, these two also will tend to be strongly linked themselves. There will be exceptions, but generally this should be the case [ … ] In a graph, this principle implies that strong links [ … ] tend to fall within triangles [ … ] Suppose somehow we could remove a strong link from the social network [ … ] Since strong links almost always appear in special triangles, you could still be able to go from one end of the missing link to the other in just two steps, by moving along the remaining two edges of the triangle. So, you can knock out any strong link without having much effect on 'social distances' within the network [ … ] The crucial links [ … ] are the weak links. You have strong links to family members, coworkers, friends, and so on. If your direct link to one of these people were removed, you would probably still be linked by a short path through common friends, other family members, and so on [ … ] However, you also have acquaintances you rarely see or contact, people you went to college with but even then didn't know very well, and so on. These are your weak links."
It is these weakly related people who become "bridges" between "clusters" of strongly related people. It is these bridges that connect you to anybody else in the world. If your 'casual acquaintance' (i.e. a weak link) in Samoa dies, you may well become completely disconnected from anybody else in Samoa. "Without weak ties, a community would be fragmented into a number of isolated cliques." (Buchanan, p. 46). Networks exhibiting this property were called "small-world networks" by Watts and Strogatz.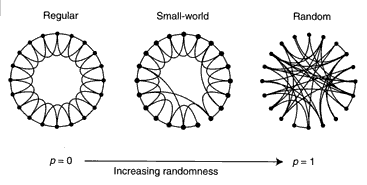
Idealized Small-World Network
The image shows how a 'regular ring lattice' (left), where each dot is connected to its four immediate neighbors, can be transformed into a small-world network (center) by changing some of the links into random ones. The image at right shows a completely randomized network. Although greatly idealized, the image in the center corresponds to the world of six degrees of separation. This model applies equally well to the 'Kevin Bacon world' we saw earlier, to the electric power grid of the Western United States, and to the 282-neuron brain of the nematode worm C. elegans, a 1mm long soil nematode of temperate regions, whose complete genome is well known. -
To see a small-world in action, visit U Wilensky's NetLogo Fireflies Model (1998).
You will find a java applet that allows you to visualize the fantastic process by which "a population of
fireflies [ … ] synchronize[s] their flashing using only the interactions between the individual
fireflies. It is a good example of how a distributed system (i.e. a system with many interacting elements, but no
'leader') can coordinate itself without any central coordinator." (To enhance the effect, you may want to set
the "show-dark-fireflies" switch to Off.)
Read
 Who Cares About Fireflies? A Talk with Steven Strogatz.
Steven Strogatz and Duncan Watts were the first to solve the long-standing mystery of the syncronized fireflies of
Papua, New Guinea.
Who Cares About Fireflies? A Talk with Steven Strogatz.
Steven Strogatz and Duncan Watts were the first to solve the long-standing mystery of the syncronized fireflies of
Papua, New Guinea.
-
I have mentioned above that even the electric power grid of the Western United States, or the brain of a living creature
appear to follow the small-world model. We don't have the time nor the resources to explore these or other
complex networks, such as the internet and the web, and other important social and technological networks. As
Buchanan puts it (p. 204), the consequences of such an approach are "not so small." It is also important
to point out that many problems remain to be solved.
Here I will briefly mention Scale-Free Networks, a special class of small-world networks.
"Scale-free networks, including the Internet, are characterized by an uneven distribution of connectedness. Instead of the nodes of these networks having a random pattern of connections, some nodes act as 'very connected' hubs, a fact that dramatically influences the way the network operates. Using a Web crawler, physicist Albert-Laszlo Barabasi and his colleagues at the University of Notre Dame in Indiana in 1998 mapped the connectedness of the Web. They were surprised to find that the structure of the Web didn't conform to the then-accepted model of random connectivity. Instead, their experiment yielded a connectivity map that they christened 'scale-free.' "The connectedness of a randomly distributed network decays steadily as nodes fail, slowly breaking into smaller, separate domains that are unable to communicate. Scale-free networks, on the other hand, may show almost no degradation as random nodes fail. With their very connected nodes, which are statistically unlikely to fail under random conditions, connectivity in the network is maintained. It takes quite a lot of random failure before the hubs are wiped out, and only then does the network stop working."
"In the random network, the five nodes with the most links (in red) are connected to only 27% of all nodes (green). In the scale-free network, the five most connected nodes (red) are connected to 60% of all nodes (green)."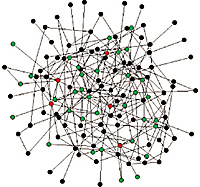
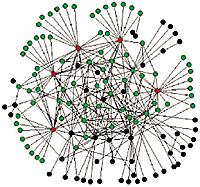
Comparing Random and Scale-Free Distribution
-
I will conclude this lecture with an intriguing statement in Buchanan's last chapter (p. 207):
"[ … ] much of the work we have explored in this book has been carried out by physicists working in areas that would not normally be considered part of physics: social and computer networks, cellular biochemistry, economics. But in this sense, physics is evolving. Where once it was only the study of matter and the laws of fundamental physics, it has graduated into the study of organization in all its forms. The study of emergence 1 in all its forms is one of the most important scientific enterprises of our era … 1 "the idea that meaningful order can emerge all on its own in complex systems made of many interacting parts." (Buchanan, p. 198)
Readings, Resources and Questions
-
Here is another recent example of the applicability of small-world networks to real systems: Small World Networks Key to Memory
"If you recall this sentence a few seconds from now, you can thank a simple network of neurons for the experience. That is the conclusion of researchers who have built a computer model that can reproduce an important aspect of short-term memory.
The key, they say, is that the neurons form a 'small world' network. Small-world networks are surprisingly common. Human social networks, for example, famously connect any two people on Earth—or any actor to Kevin Bacon—in six steps or less." -
A very good overview is offered by P Shulman in the December 1998 issue of Discovery Magazine:
 From Muhammad Ali to Grandma Rose..
From Muhammad Ali to Grandma Rose..
-
The literature on social networks is vast. Here are a couple of very good, accessible books:
- Albert-László Barabási, Linked: The New Science of Networks. Perseus Publishing, 2002
- Mark Buchanan, Nexus: Small Worlds and the Groundbreaking Theory of Networks. W W Norton & Co, 2002.
- Steven Strogatz, Sync: The Emerging Science of Spontaneous Order. Theia Books, 2003.
- Duncan J Watts, Six Degrees: The Science of a Connected Age. W W Norton & Co, 2003.
- Check also the Small World Phenomenon entry in Wikipedia, where you will also find additional references. Here is a good collection of links to articles on Scale-Free / Power Law Networks. The articles are generally quite technical, but you may find them useful when comparing the original scientific discourse with the 'English' version presented here.
- Read D J Watts' article The Internet, The Small World, and The Nature of Distance, Boston Science Museum Exhibit on Messages (May 1999). Unfortunately this article does not seem to be available any longer.
-
Here is an example of a special type of degree of separation:
"Most practicing mathematicians are familiar with the definition of one’s Erdös number [ … ] Paul Erdös (1913–1996), the widely-traveled and incredibly prolific Hungarian mathematician of the highest caliber, wrote hundreds of mathematical research papers in many different areas, many in collaboration with others. His Erdös number is 0. Erdös’s co-authors have Erdös number 1. People other than Erdös who have written a joint paper with someone with Erdös number 1 but not with Erdös have Erdös number 2, and so on." [ from The Erdös Number Project ]
For an amusing twist, see Thumbing His Nose at Academe, a Scholar Tries to Auction His Services:"Late last month an independent scientist auctioned off his services as a co-author on eBay, with the promise of helping the highest bidder write a scientific paper for publication. The offer even had the added allure of a linkage with the legendary mathematician Paul Erdös [ … ] The auction began as a bit of fun, admits William A Tozier, a consultant in Ann Arbor, Mich., who specializes in machine learning and artificial-intelligence research. "I undertook it as a combination of a joke and conceptual art and a bit of an experiment in social networks," he says. The idea builds on the reputation of Erdös, a Hungarian mathematician who died in 1996. A prolific researcher, with more than 1,400 published papers, he spent the last several decades of his life moving from one colleague's house to another's, staying for extended periods at each place and collaborating on solving problems."
-
Here is an example of application of the small-world model to technology: Circuits are Small Worlds
"Recent theoretical studies and extensive data analyses have revealed a common feature displayed by biological, social, and technological networks: the presence of small world patterns. Here we analyze this problem by using several graphs obtained from one of the most common technological systems: electronic circuits. It is shown that both analogic and digital circuits exhibit small world behavior. We conjecture that the small world pattern arises from the compact design in which many elements share a small, close physical neighborhood plus the fact that the system must define a single connected component (which requires shortcuts connecting different integrated clusters) …"
[ from Topology of Technology Graphs: Small World Patterns in Electronic Circuits ] -
C Kelty, at Rice University, in Stanley Milgram's Small World Experiment, poses
very interesting questions:
"Milgram and the science of social networks focuses on the network itself, especially the complex ones. It is not interested in what anthropologists have traditionally focussed on, namely the kinship relations of the people involved. What's the difference?
To begin with, there is a classic distinction in anthropology. Emic vs Etic. The explanation that we as observers give of any phenomena can be different from the explanation that those observed themselves might give [ … ] The small world problem doesn't capture this difference [ … ] However, the anthropological question does not go away. Just as people can describe their relationships with each other on the basis of their understanding of biology, so too might they describe their relations on the basis of their understanding of a network. The phrases 'six degrees of separation' and 'it's a small world after all' are just two examples of such explanations. Some people who understand how the internet and the telecommunications system work might have a different understanding of the shape of society from those people who only ever talk with their neighbors and the mail man. What difference does it make to have a different understanding of the shape of society?" - Material related to these topics can be found in Lecture 3.
© Copyright Luigi M Bianchi 2003-2005
Picture Credits: Physics Central · Owen Densmore
Santa Fe Institute · ComputerWorld
Last Modification Date: 25 October 2005
Picture Credits: Physics Central · Owen Densmore
Santa Fe Institute · ComputerWorld
Last Modification Date: 25 October 2005