One meteorologist remarked that if the theory were correct,
one flap of a seagull's wings would be enough
to alter the course of the weather forever.

Edward Lorenz, as quoted in Michael Cross' The Butterfly Effect.

"For want of a nail, the shoe was lost;
For want of a shoe, the horse was lost;
For want of a horse, the rider was lost;
For want of a rider, the battle was lost;
For want of a battle, the kingdom was lost!"

Quoted in James Gleick's Chaos: Making a New Science (p. 23. Penguin Books, 1988).

Topics

• "The world of mathematics has been confined to the linear world for centuries. That is to say, mathematicians and physicists have overlooked dynamical systems as random and unpredictable. The only systems that could be understood in the past were those that were believed to be linear, that is to say, systems that follow predictable patterns and arrangements. Linear equations, linear functions, linear algebra, linear programming, and linear accelerators are all areas that have been understood and mastered by the human race. However, the problem arises that we humans do not live in an even remotely linear world; in fact, our world should indeed be categorized as nonlinear; hence, proportion and linearity is scarce. How may one go about pursuing and understanding a nonlinear system in a world that is confined to the easy, logical linearity of everything? This is the question that scientists and mathematicians became burdened with in the 19th Century; hence, a new science and mathematics was derived: chaos theory." [ Manus J Donahue in Chaos and Trend Following ]

  Let's examine this statement in some detail. A system is considered linear if, when you double the input, the output doubles too. For example, place an object on a scale. The device will indicate some value X. Replace now the object with two copies of it. The scale should indicate 2X. If this is the case for several different objects, the scale is said to be linear—at least within the range of weights corresponding to such objects. Here is another example. Stretch a piece of wire by applying a certain force to it. Within a certain range of applied forces, if you double the force, you double also the amount by which the wire stretches. Beyond a certain point, however, this is no longer the case, so that, when you double the applied force, the wire stretches by more than twice the previous value. In this range of applied forces, the wire behaves non-linearly.

  "In mathematics and physics, chaos theory deals with the behaviour of certain nonlinear dynamical systems that (under certain conditions) exhibit the phenomenon known as chaos, most famously characterised by sensitivity to initial conditions (see butterfly effect). Examples of such systems include the atmosphere, the solar system, plate tectonics, turbulent fluids, economies, and population growth. Systems that exhibit mathematical chaos are deterministic and thus orderly in some sense; this technical use of the word chaos is at odds with common parlance, which suggests complete disorder." [ from Wikipedia ]

  Keep in mind that it is much easier to describe (mathematically and otherwise) linear systems than non-linear systems. That's why only relatively recently has science started tackling non-linear systems, despite the fact, pointed out by Donahue, that most interesting, real systems are indeed non-linear.
  In order to discuss the definition given above, it may be useful to consider a few examples of chaotic systems. The first one is the solar system (and probably any other solar system). Here is a good description of the situation by Nigel Bunce and Jim Hunt:

  "When Newton published his great laws of gravitation and mechanics in the seventeenth century, the proving ground for these laws was the solar system. Newton showed that the clockwork-like repeating motions of the planets, and all other members of the solar system, were explained and predicted by simple quantitative laws. His laws were shown to be the basis of all motion and for a long time were thought to be the basis of all physical phenomena. The basic philosophy in the Newtonian universe is that, given the position and state of motion of all the particles in the universe at some instant, the state of the universe can be predicted any time into the future or back into the past.
  [ … ]
  What was not realized until late in the nineteenth century was that there were cases where the uncertainties in the calculation could grow so rapidly that the future motion of the system was, in principle, completely unpredictable and chaotic.
  [ … ]
  Two theorists at Massachusetts Institute of Technology, G J Sussman and J Wisdom, have made elaborate and accurate calculations of the motion of the planet Pluto over a period of 845 million years, which is about one sixth of the age of the solar system. Pluto is our strangest planet, with a very eccentric and highly tilted orbit. Their calculations show that the motion of Pluto is not infinitely calculable but is, in fact, chaotic! Even more surprising is that the chaotic nature of its motion requires only 200 million years to become evident. This means that the motion of Pluto cannot be predicted more than 200 million years into the future or back into the past. This is a very short time compared with the age of the solar system." [ from The Solar System in Chaos ]

  Similar calculations have been performed since, and they all show that not only Pluto's orbit, but the entire solar system is chaotic. For instance, it is possible that sometime in the future Mercury and Venus collide, even though at present they appear to follow seemingly stable and distinct orbits.
  A second example comes from the study of populations, specifically the so-called logistic equation, which was first introduced by Pierre F Verhulst in 1838. The assumptions behind such equation (already formulated by Thomas Malthus in his Essay on the Principle of Population (1798)), are deceptively simple. Everything else being equal, a) the rate of reproduction is proportional to the existing population; and b) the rate of reproduction is proportional to the amount of available resources. Although both assumptions seem to involve proportionality, i.e. linearity, their combination is non-linear, and is controlled by a number or parameter the value of which corresponds to wildly different behaviors of the population. Here is Gleick's description of what biologist Robert May found:

  "When the parameter was low, May's simple model settled on a steady state. When the parameter was high, the steady state would break apart, and the population would oscillate between two alternating values. When the parameter was very high, the system—the very same system—seemed to behave unpredictably." [ from Gleick, op. cit., p. 70 ]

  and the so called logistic map, which renders Gleick's description graphically: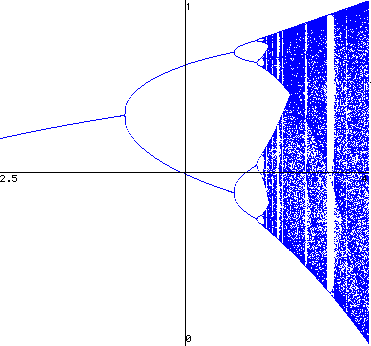

   

  

  The Logistic Map

   

  Finally, as a third, live example, consider two identical double pendulums. Follow the animation, and notice that any, unavoidable, difference in the way the two systems are set in motion, results in two completely different behaviors [ from Marc Spiegelman's An Introduction to Dynamical Systems and Chaos ]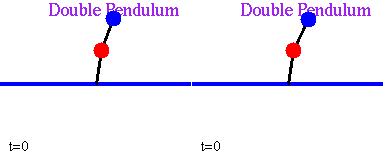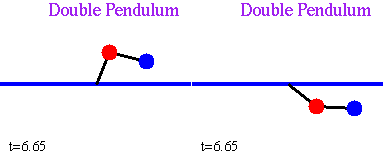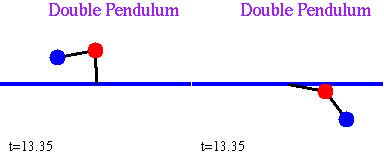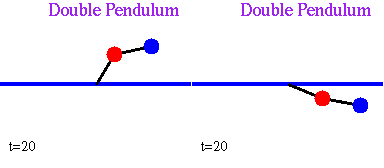

   

  

  Two Identical Pendulums with Slightly Different Initial Conditions

   

• In all these examples the systems in question are non-linear, and they share the fundamental property that their behavior is crucially sensitive to their initial conditions. This is what the butterfly effect is about. A fluttering butterfly near one of the two pendulums will change ever so slightly their initial speeds, and very likely it will affect them ever so slightly in different ways. In chaotic systems, such infinitesimal differences will become magnified in the course of time, leading to completely unrelated behaviors. Of course there is no need for an actual butterfly to be present. Our measurements are always subject to errors, no matter how precise we try to be; the forces we (or nature) apply to systems can never be reproduced exactly; and so on. Yet, chaotic system can be completely deterministic, in the sense that "no randomness is involved in the development of future states of the system" [ from Wikipedia ].
  Perhaps a useful way to elaborate the above is to consider what, historically, represents the first encounter between chaos and computers. I am referring to the somewhat accidental discovery made by Edward Lorenz that the weather is a chaotic system. This discovery was published in 1963 in the Journal of the Atmospheric Sciences (v 20, pp 130-41). Lorenz was a meteorologist and, like many of his colleagues, was trying to model Earth's atmosphere. Frustrated by the enormous complexity of the problem, he wondered whether there could be something to be gained in resorting to a very simplified representation. His final model involved only three, rather elementary, equations. To appreciate the level of simplification he indulged in, keep in mind that modern global weather models involve hundreds of thousands of very complex equations! What Lorenz tried to do was to see what could be gained by modeling the convective motion of a volume of air "which is warmed from below and cooled from above" [ from Lorenz Equation ]

  dx/dt = ς(y - x)
  dy/dt = x(τ - z)
  dz/dt = xy - β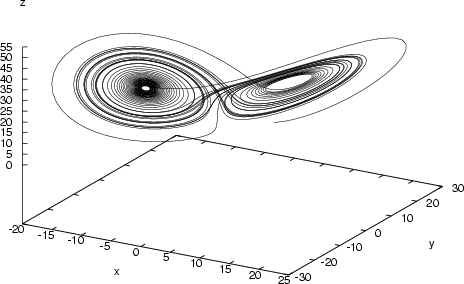  

   

  

  The Lorenz Attractor, or the Solution of Lorenz' Equation

   

  "ς, τ and β are physical constants; x is proportional to the intensity of the convective motion, while y is proportional to the temperature difference between the ascending and descending currents, similar signs x and y denoting that warm fluid is rising and cold fluid is descending. The variable z is proportional to the distortion of vertical temperature profile from linearity, a positive value indicating that the strongest gradients occur near the boundaries." [ from Lorenz Equation ]

  To appreciate better the chaotic nature of this motion, here is a Java applet that, once you click on the initially empty rectangle, shows the time-evolution of the curve itself. Now, click again on a point close to the one on which you clicked earlier. Follow the evolution of the two trajectories. You will see that eventually the two paths will diverge and become unrelated.

   

  The Lorenz 'Butterfly' in Action
  [ Used with permission. © 1996, James P. Crutchfield. All rights reserved.]
  In summary, you can read   the terse statement by one of the pioneers in this field, Michael Feigenbaum, head of the Laboratory of Mathematical Physics at Rockefeller University.
• A final note. You may wonder about the advantages, if any, of chaotic systems over their non-chaotic counterparts. This is not just an 'academic' question. Here is Gleick's answer , which I hope will give rise to a good discussion in class.

  "Sensitive dependence on initial conditions serves not to destroy but to create. As a growing snowflake falls to earth, typically floating in the wind for an hour or more, the choices made by the branching tips at any instant depend sensitively on such things as the temperature, the humidity, and the presence of impurities in the atmosphere. The six tips of a single snowflake, spreading within a millimeter space, feel the same temperatures, and because the laws of growth are purely deterministic, they maintain a near perfect symmetry. But the nature of turbulent air is such that any pair of snowflakes will experience very different paths. The final flake records the history of all the changing weather conditions it has experienced, and the combinations may well be infinite.
  Snowflakes are nonequilibrium phenomena, physicists like to say. They are the product of imbalance in the flow of energy from one place to another. The flow turns a boundary into a tip, the tip into an array of branches, the array into a complex structure never before seen. As scientists have discovered such instability obeying the universal laws of chaos, they have succeeded in applying the same methods to a host of physical and chemical problems, and, inevitably, they suspect that biology is next."
  [ from op. cit., pp. 311 - 314 ]

  The basic idea is that the very unpredictability of chaotic systems endows such systems with great flexibility. This is particularly important in biological systems. It should not come as a surprise, therefore, that the brain, for example, shows definite signs of chaotic behavior, especially in healthy individuals.

  "Deterministic chaos is characterized by complexity that is self-organized according to internal constraints. Examples occur at all levels of organization of nervous systems, from single neurons through neural networks up to whole brains. The search for the constraints is enabled by use of the theory of chaos to model neural functions. The level of greatest interest for modeling by cognitivists is that of the limbic system, because in animals from fish to man that is where the organization of voluntary behavior occurs. Chaotic dynamics can account for its flexibility and creativity. Our observations of the electrical activity of the brain during intentional behavior give us a window onto essential parts of the intentionality of the subject. The term is used here in one of two currently debated meanings, deliberately in order to advance the claim that biological measurements of brain function will help to resolve some centuries-old philosophical disputes about the nature of the fundamental processes of the mind."
  [ from Walter Freeman's Chaos in the CNS: Theory and Practice ]

 
Readings, Resources and Questions

• Lectures 3 and Lectures 6 include some material relevant to the present lecture.
• Perhaps the easiest and best introduction to chaos is James Gleick's Chaos: Making a New Science (Penguin Books, 1988). See also his home page.
• Read through   What is Chaos? A Five-Part Online Course for Everyone.  A somewhat more technical, yet still understandable—if you skip the math—resource is George T Yurkon's Introduction to Chaos and Its Real World Applications.
• Visit the very interesting Turbulent Landscapes—A Dialogue between Jim Crutchfield and Ned Kahn. "Turbulent Landscapes: The Natural Forces That Shape Our World [ was a ] landmark exhibition, funded by the National Science Foundation, [ which presented ] works that use the forces of nature to capture and expose the complex and seemingly chaotic processes of nature—whirlpools, swirling sandstorms, eroding cliffs, avalanches, tornados."
• Read W L Ditto and L M Pecora, Mastering Chaos. This article appeared in the August 1993 issue of Scientific American (pp. 78 - 84). Here is the abstract: "It is now possible to control some systems that behave chaotically. Engineers can use chaos to stabilize lasers, electronic circuits and even the hearts of animals."