Symmetry establishes a ridiculous and wonderful cousinship
between objects, phenomena and theories outwardly unrelated:
terrestrial magnetism, woman's veils, polarized light, natural selection,
the theory of groups, structure of space, vase designs, quantum physics,
scarabs, flower petals, X-ray interference patterns, cell division in sea urchins,
equilibrium positions of crystals, Romanesque cathedrals, snowflakes, music,
the theory of relativity … "

[ Hermann Weyl, quoted in Symmetry: Life's Search For Immortality ]

It is the symmetry which creates the phenomenon.

[ Pierre Curie, 1894, quoted in The Curie Principle ]

Topics

• The image below is just one of hundreds of similar ones that Ernst Haeckel (1834-1919) manually (copper plates) created from direct observation (often by means of microscopes). The organisms shown exhibit and illustrate all sorts of symmetries. Another work by Haeckel is also online: Ernst Haeckel: Die Radiolarien (Rhizopoda Radiaria). Berlin, 1862. You may further like to visit The Wandtafeln of Rudolph Leuckart (1822-1898), another great zoologist and illustrator.

   

  

  From Ernst Haeckel : Kunstformen der Natur 1899-1904

   

  To quote again Hermann Weyl (1885 - 1955), "Symmetry, as wide or narrow as you may define its meaning, is one idea by which man through the ages has tried to comprehend and create order, beauty, and perfection." [ from Quotations by Hermann Weyl ]. So, what is symmetry?

  "Symmetry is a characteristic of geometrical shapes, equations and other objects; we say that such an object is symmetric with respect to a given operation if this operation, when applied to the object, does not appear to change it. The three main symmetrical operations are reflection, rotation and translation. A reflection "flips" an object over a line, inverting it to its mirror image, as if in a mirror. A rotation rotates an object using a point as its center. A translation "slides" an object from one area to another by a vector. Even more complex operations on a geometric object, like shrinking or shape warping, can be reduced to the operation of translation of every point within the object. Symmetry occurs in geometry, mathematics, physics, biology, art, literature (palindromes), etc." [ from Wikipedia, Symmetry ]

  Notice, first of all, that something is symmetric always relative to a specific operation or transformation. For example, the five-point star creature in the lower right-hand side of the picture above is symmetric relative to a rotation of 72° (1/5 of 360°) around an axis passing through the center of the star, and perpendicular to the page. You rotate the star by such an angle and what you get is something completely indistinguishable from the original image. Conversationally, however, we often say that something is symmetric without further qualifications.

  "If I am not mistaken, the word symmetry is used in our everyday language in two meanings. In the one sense symmetric means something like well-proportioned, well-balanced, and symmetry denotes that sort of concordance of several parts by which they integrate into a whole. Beauty is bound up with symmetry. Thus Polykleitos, who wrote a book on proprotion and whom the ancients praised for the harmonious perfection of his sculptures, uses the word, and Dürer follows him in setting down a canon of proportions for the human figure." [ from Hermann Weyl, Symmetry (Princeton U Press, 1952, p. 3 ]

  In this lecture, therefore, we will always use the term symmetry in the precise sense defined above, even though one can argue that the popular use of the term is ultimately related to the more technical definition.
  Notice also that the concept of symmetry, as defined above (and as anticipated in the epigraph of this lecture), can apply to almost anything. For instance, the sentence "a man, a plan, a canal, Panama" reads the same from left or from right, if we disregard punctuation, spaces and capitals. In other words, this sentence is symmetrical relative to a switch of reading direction from left-to-right to right-to-left which ignores punctuation, spaces and capitals.
  If we limit ourselves, at least for the moment, to geometric figures in the plane, the most common transformations we can apply to them are rotations (by a given angle around a given axis), reflections (mirror image), and translations (by a given distance in a given direction). Sometimes two further transformations are included: glide reflections (reflection plus a translation along the mirror axis) and identity. The latter is a transformation which consists in doing … nothing! For a more graphical version of these transformations, see The Four Types of Symmetry in the Plane. In three dimensions things get more complicated, of course, but for simplicity we will confine ourselves to the 2-dimensional plane.
  The best way to understand these concepts is to apply them to actual objects, such as the images of the various organisms drawn by Haeckel (see figure above). Which symmetries does each one of them have?
• Perhaps the easiest way to enter the rich world of symmetry is to consider a classical problem. Suppose you wish to know how many ways are there to create a frieze? A frieze is an infinite strip filled with some sort of pattern. Here are examples from the frescos in Castello Sforzesco in Milan

   

  
  
  
  
  
  
  
  
  
  
  
  
  
  

  The Seven Types of Friezes. Castello Sforzesco, Milan, Italy

   

  Only seven? Yes! It can be proven mathematically that only seven different arrangements are possible.
  The next step would be to ask a similar question about wallpapers. Once again, it does not matter whether you want images of elephants or frogs on your walls. No matter what choice you make, there are only seventeen different ways of arranging wallpaper patterns. For nice and original examples, visit Hans Kuiper's 17 Wall Paper Symmetry Groups to Create a Regular Division of the Plane. Here are illustrations from Japanese traditional arts and crafts [ from Seventeen Kinds of [Japanese] Wallpaper Patterns ]

   

  
  
  
  
  
  
  

  The Seventeen Types of Wallpapers. Japanese Art.

   

  The great explorers and masters of the art of friezes and wallpapers were (and in many ways they still are) Islamic artists. One important reason for their excellence is that Islamic art does not allow the visual representation of living creatures. Instead ir relies heavily on abstract geometric patterns.

   

  

  Detail from the Alhambra, Granada, Spain

   

  Obviously the world does not consist only of wallpaper, and much more can be said about the symmetries of 2- and 3-dimensional abstract and concrete objects. See for example Kim Williams' Symmetry in Architecture, and Wallpaper Patterns Or, if you are more adventurous, visit Don Hatch's Hyperbolic Planar Tesselations, from which the illustration below is reproduced.

   

  

  An Example of Hyperbolic Planar Tesselation

   

  Friezes and wallpapers are chapters in a much broader story, tessellation or tiling, i.e. the various ways, say, an infinite plane can be covered with finite shapes that fit together without gaps or overlaps. Here is a famous tiling problem. In how many ways can the plane be tiled with a regular polygon? A regular polygon is a polygon all of whose sides and angles are the same. Squares and equilateral triangles are instances of regular polygons. It turns out that the plane can be tiled only with equilateral triangles, squares and hexagons. See for example Tessellations.
• Let us now return to the basic concept of symmetry and examine briefly why symmetry is of fundamental importance not only in purely geometrical contexts, but in science in general, and in physics in particular.
  From a purely mathematical point of view (with lots of concrete applications, however), symmetry can be taken as the point of departure of much of geometry, as opposed to being just an application of other principles. This was first proposed by Felix Christian Klein (1849 – 1925), who in 1872, in what is now called the Erlangen Program, suggested that symmetry should be the defining feature of geometry. To understand the idea, notice that the 19th century saw the discovery of new, non-Euclidean geometries, and the need to systematize this rapidly growing zoo was the main motivation that led Klein to his program.

  "Was there one 'geometry' or many? Since Euclid, geometry had meant the geometry of Euclidean space of two dimensions (plane geometry) or of three dimensions (solid geometry). In the first half of the nineteenth century there had been several developments complicating the picture. Mathematical applications required geometry of four or more dimensions …

  The solution in abstract terms was to use symmetry as an underlying principle, and to state first that different geometries could co-exist, because they dealt with different types of propositions and invariances related to different types of symmetry and transformation." [ from Felix Christian Klein ]

  In other words, and to greatly oversimplify things, a given geometry differed from another fundamentally in terms of the transformations under which their respective contents would be left unchanged.
  This kind of approach was very successful and became one of the methods of choice not only in mathematics, but in physics too.
• A second crucial point in the history of symmetry was the discovery by Emmy Amalie Noether (1882 - 1935) of what is now called Noether's Theorem. This theorem states that to every symmetry, there corresponds a conservation law and vice versa.

  "In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves." [ from Noether's Theorem ]

  Here are some examples, stated rather simply, without qualifications: conservation of the electric charge, conservation of energy, conservation of moment and angular momentum, etc. The fact that the equations of physics are symmetric with respect to a switch between past and present entails that energy is conserved. The fact that the equations of physics are symmetric with respect to any translation in space entails that linear momentum is conserved. And so on. This is indeed remarkable! The well known fact that you can not create or destroy energy+mass (remember that energy and mass can transform into each other, as Einstein showed) is a reflection of the properties of space and time.
• I will conclude this lecture with a short discussion of what seems at first to be a simple paradox. The fertilized eggs from which you and I come from is essentially spherically symmetric. Even after a few cellular divisions, the embryo seems to consist of a number of identical, spherically symmetric cells. Yet, we know we are not spherically symmetric, but only, approximately, bilaterally symmetric. How can that be? What causes the egg to lose its symmetry? This loss is known as symmetry breaking.

   

  

  Leonardo da Vinci, Vitruvian Man, 1513

   

  Consider a simple case:

  "A common example to help explain this phenomenon is a ball sitting on top of a hill. This ball is in a completely symmetric state. However, it is not a stable one: the ball can easily roll down the hill. At some point, the ball will spontaneously roll down the hill in one direction or another. The symmetry has been broken because the direction the ball rolled down in has now been singled out from other directions." [ from Spontaneous Symmetry Breaking ]

  To say "spontaneous" is somewhat misleading. Clearly the ball will need a little nudge, otherwise it would remain where it is, and keep the symmetries it has. If you wish to consider a less trivial case, think of the universe. The primeval fireball which gave rise to the big bang likely had more symmetries than the universe exhibits now. In this case it is rather more difficult to imagine what "a little nudge" might have been. We can not of course delve into such topics at any length. Here I will only mention a few basic considerations.

  "The study of symmetry breaking [ … ] goes back to Pierre Curie. According to Curie, symmetry breaking has the following role: for the occurrence of a phenomenon in a medium, the original symmetry group of the medium must be lowered (broken, in today's terminology) to the symmetry group of the phenomenon [ … ] by the action of some cause. In this sense symmetry breaking is what “creates the phenomenon”. Generally, the breaking of a certain symmetry does not imply that no symmetry is present, but rather that the situation where this symmetry is broken is characterized by a lower symmetry than the situation where this symmetry is not broken.

  Symmetry breaking was first explicitly studied in physics with respect to physical objects and phenomena. This follows naturally from the developments of the theory of symmetry, at the origin of which are the visible symmetry properties of familiar spatial figures and everyday objects. However, it is symmetry breaking of the laws that has come to have greater significance in physics. There are two different types of symmetry breaking of the laws: 'explicit' and 'spontaneous,' the case of spontaneous symmetry breaking being the more interesting from a physical as well as a philosophical point of view.

  Spontaneous symmetry breaking [ … ] occurs in a situation where, given a symmetry of the equations of motion, solutions exist which are not invariant under the action of this symmetry without any explicit asymmetric input (whence the attribute 'spontaneous'). A situation of this type can be first illustrated by means of simple cases taken from classical physics. Consider for example the case of a linear vertical stick with a compression force applied on the top and directed along its axis. The physical description is obviously invariant for all rotations around this axis. As long as the applied force is mild enough, the stick does not bend and the equilibrium configuration [ … ] is invariant under this symmetry. When the force reaches a critical value, the symmetric equilibrium configuration becomes unstable and an infinite number of equivalent lowest energy stable states appear, which are no longer rotationally symmetric but are related to each other by a rotation. The actual breaking of the symmetry may then easily occur by effect of a (however small) external asymmetric cause, and the stick bends until it reaches one of the infinite possible stable asymmetric equilibrium configurations." [ from Symmetry and Symmetry Breaking ]

  Perhaps the most famous case of symmetry breaking in modern science is the demise of parity, in 1956. A very good account is given by Krishna Myneni in Symmetry Destroyed: The Failure of Parity. Another great resource is The Fall of Parity.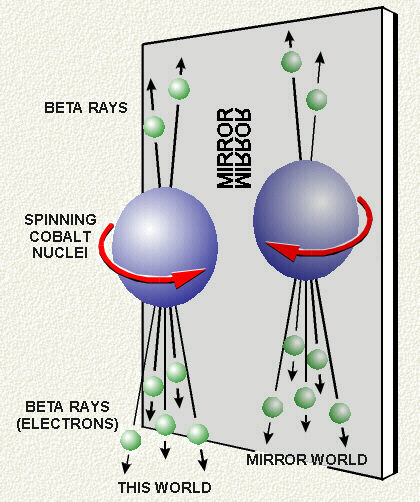

   

  

  The mirror world is distinguishable from the real world

   

  Until the early 50's it had been universally accepted that the universe essentially enjoyed mirror symmetry, that its laws had no preference for left or right.

  "The preference we give to right over left is a mere human convention—physicists had assumed. Nature could not possibly have made such a distinction, whether in favor of right or of left. To be sure, her organic creations on this planet are not perfectly symmetric: our hearts are on the left sides of our bodies, our intestines do all wind in the same sense, and many chemicals synthesized by plants and animals have a definite handedness. But the advance of physical theory has been so closely connected, historically, with the endeavor to free our conceptions of the world about us from all parochialisms, that physicists have grown allergic to concepts which appear to have no better basis than their accordance with our accustomed ways of viewing our everyday experiences." [ from The Fall of Parity ]

  Instead, a clever experiment with Cobalt-60 by Chien-Shiung Wu showed otherwise. A subsequent, painstaking analysis of the experiment by T D Lee and C N Yang showed the result of the experiment (a general version of which they had suggested earlier) to be genuine and valid. There are situations in the universe which do show a preference for a certain handedness. For example neutrinos only come as left-handed particles!

  "The failure of the physicists' intuition had been enormous. Nature, as it had done with relativity, did not oblige itself to follow the rules of 'common sense.' To physicists, results of the Columbia experiments left them in a profound quagmire: Why did nature distinguish between the left and the right? Though the question remains unanswered, the physicists had set themselves up for the shock. They had ignored Ernst Mach's warning: 'Even instinctive knowledge of so great a logical force as the principle of symmetry may lead us astray … The instinctive is just as fallible as the distinctly conscious. Its only value is in provinces with which we are very familiar.' The new province of weak interactions had not been tested before Lee and Yang made the suggestion. Nevertheless, the physicists' assumption that nature will present a simple understanding is unflailing. Chen Ning Yang has stated, 'In the study of nature, one believes in something simple underlying all.' Madame Wu agrees, 'One hopes that nature possesses an order that one may aspire to comprehend. When we arrive at an understanding, we shall marvel how neatly all the elementary particles fit into the great scheme.' Violation of the law of conservation of parity, then, should lead one to search for an even more fundamental symmetry to the universe." [ from Symmetry Destroyed: The Failure of Parity ]

 
Readings, Resources and Questions

• The classical, somewhat introductory, book on symmetry is Herman Weyl's Symmetry (Princeton U Press, 1952).
  Another classic is Richard Feynman's The Character of Physical Law (MIT Press, 1965). In particular, Chapter 5, Symmetry in Physical Law, is a beautifully clear introduction to symmetry and conservation laws in physics.
  A concise, yet excellent statement on parity is Kyle Cranmer's Symmetry.

  Browse through Helmer Aslaksen's course on Mathematics in Art and Architecture.

• Tilings and Tesselations is a good and rather simple introduction to the topic, with clear, intuitive illustrations. A similar, good site is Symmetry and Tessellations.
  Ana Kozomara's Discrete Plane Symmetry Groups offers a rather technical introduction, but her illustrations are very clear and useful.
• The classical introduction to parity and its fall is Martin Gardner's The New Ambidextrous Universe. Symmetry and Asysmmetry from Mirror Reflections to Superstrings (3rd Revised ed., W H Freeman and Company, NY, 1964). This book was written for the layman, and it is incredibly enjoyable and exciting.