Topics

• "Shannon's work, as well as that of his legion of disciples, provides a crucial 'knowledge base' for the discipline of communication engineering. The communication model is general enough so that the fundamental limits and general intuition provided by Shannon theory provide an extremely useful 'roadmap' to designers of communication and information storage systems. For example, the theory tells us that English text is not compressible to fewer than about 1.5 binary digit per English letter, no matter how complex and clever the encoder/decoder. Most significant is the fact that Shannon's theory showed how to design more efficient communication and storage systems by demonstrating the enormous gains achievable by coding, and by providing the intuition for the correct design of coding systems. The sophisticated coding schemes used in systems as diverse as 'deep-space' communication systems (for example NASA's planetary probes), and home compact disk audio systems, owe a great deal to the insight provided by Shannon theory. As time goes on, and our ability to implement more and more complex processors increases, the information theoretic concepts introduced by Shannon become correspondingly more relevant to day-to-day communications."
                                                                               Aaron D Wyner

• The machines described in the previous lecture were of course just the beginning, and many more were built in the subsequent years. To avoid reducing history to a catalog of events and objects, I will only suggest, in the Readings, Resources and Questions section, resources where the most important of these machines are described, and focus instead on more important theoretical and technological milestones.
  Probably the most important of such milestones was the publication in 1948 by Claude Elwood Shannon (1916 - 2001) of  A Mathematical Theory of Communication. While the original paper may be a bit too technical, you can read   Brief Excerpts from Warren Weaver’s Introduction to: Claude Shannon’s The Mathematical Theory of Communication and Aaron D Wyner's The Significance of Shannon's Work. A rather good summary of the communications side of Shannon's paper is The Shannon-Weaver Model. Finally, a useful resource is Bell Labs Celebrates 50 Years of Information Theory.
• The word information is used everywhere. 'Information technology' (and its acronym 'IT'), 'the information age,' 'the information revolution,' and other variations on the theme, are waved about like flags. We also know that information and computers somehow belong together. It is therefore necessary to ask ourselves if the concept behind this word is indeed still the familiar one. Is information just another term for facts, experience, knowledge? Although the two concepts are by no means identical, we will assume as a given that information and communication are related. For example, in The Evolution of Communication (The MIT Press, 1997, p. 6), Marc Hauser writes: "The concepts of information and signal form integral components of most definitions of communication… Thus information is a feature of an interaction between sender and receiver. Signals carry certain kinds of information content, which can be manipulated by the sender and differentially acted upon by the receiver.." Statements such as this seem pretty clear, but they are qualitative, and may not be suitable in situations where it is necessary to quantify information, signals, etc. This is obviously the case when we deal with computers, but it is also true of other, perhaps humbler, devices that process information, such as the telegraph. Various attempts to sharpen the concept of information were thus made, beginning in the first part of the 20th century. For instance, in 1917 and later in 1928, Harry Nyquist (1889 - 1976) found the theoretical limits on how much information can be transmitted with a telegraph, and the frequency band (or bandwidth) needed to transmit a given amount of information. In particular, he "showed that to distinguish unambiguously between all signal frequency components we must sample at least twice the frequency of the highest frequency component." In the case of the telegraph, Nyquist defined information in terms of number of dots and dashes a telegraph system can exchange in a given time.
  In 1928, Ralph Vinton Lyon Hartley (1888 - 1970) defined the information content of a message as a function of the number of messages which might have occurred. For example, if we compare two situations, one in which six messages are possible, and another in which fifty-two messages are possible (think of a dice, and of a deck of cards, respectively), Hartley would say that a message about which face of the dice came up would carry less information than a message about which card came up on top of the deck of cards. Hartley suggested that the logarithm would be the most 'natural' choice for such function, "because time, bandwidth, etc. tend to vary linearly with the logarithm of the number of possibilities: adding one relay to a group doubles the number of possible states of the relays. In this sense the logarithm also feels more intuitive as a proper measure: two identical channels should have twice the capacity for transmitting information than one." [ from Hartley Information ]
• In 1948, Claude Shannon, and American engineer, took a fresh look at information from the point of view of communication. For Shannon, not unlike Hartley, "information is that which reduces a receiver's uncertainty." In a given situation, any message can be thought of as belonging to a set of possible messages. For example, if I ask a weather forecaster how's the sky over a certain region, the possible answers I could receive would be something like 'clear,' 'partly cloudy,' or 'overcast.' Before I get the answer, I am uncertain as to which of the three possibilities is actually true. The forecaster's answer reduces my uncertainty. The larger the set of possible messages, the greater is the reduction of uncertainty. If the set contains only one possibility, then I already know the answer, I am certain about it, and Shannon would say that no information is conveyed to me in this case by the actual answer. This last observation is important, because in our daily lives we may not be inclined to accept it. A message may not contain any new factual information, but the expression of my interlocutor's face or the tone of his voice do carry information that is meaningful to me. We must distinguish therefore between the vernacular sense of information, and the technical one used in telecommunications. As it always happens in science, to quantity the description of a phenomenon makes that description usable in a precise, predictable, controllable way. But this happens at the expenses of many of their familiar denotations and connotations. That's what we mean when we complain that science is drier, poorer than life. To make concepts unambiguous, so that they can be logically manipulated, we have no choice but to discard the ambiguities that language allows.

   

  

  Claude Elwood Shannon

   

  For Shannon therefore information is a form of processed data about things, events, people, which is meaningful to the receiver of such information because it reduces the receiver's uncertainty. Here is another way to express Shannon's definition: "The more uncertainty there is about the contents of a message that is about to be received, the more information the message contains. [ Shannon ] was not talking about meaning. Instead, he was talking about symbols in which the meaning is encoded. For example, if an AP story is coming over the wire in Morse code, the first letter contains more information than the following letters because it could be any one of 26. If the first letter is a 'q' the second letter contains little information because most of the time 'q' is followed by 'u'. In other words, we already know what it will be." [ from Information Theory Notes ]
• Shannon formalized this definition in a formula which is now so famous that it deserves at least one appearance in these lectures:  H = log₂(n)  . H denotes the quantity of information carried by one of n possible (and equally probable, for simplicity) messages; log₂(n) is the logarithm in base 2 of n. For example, log₂(8) = 3, log₂(32) = 5, etc. Notice in particular that when n = 1, then H = 0. In words, when a given message is the only possible one, then no information is conveyed by such message. Notice also that if there are only two possible messages, say 'yes' and 'no,' then the amount of information of each message will be  H = log₂(2) = 1. In this case we say that the message carries 1 bit of information. The word 'bit' is a contraction of the expression 'binary digit.'
  One of the fundamental results obtained by Shannon was that H = log₂(n) represents the maximum quantity of information that can be carried by a message. Noise and other factors will usually reduce the actual quantity.
• Finally, here is Shannon's model of the communication process. What happens when two people, or (more appropriately—since we are confining ourselves to 'machine communication' here) two computers or two telegraph posts communicate? They do exchange messages, of course. But there is more. For example, two people may be speaking to each other on a subway car during rush hour, and the surrounding buzz may make their conversation difficult. Or lightning may introduce spurious signals in the telegraph wires. Or the cat may have spilled some milk on your newspaper smudging some of the words. In fact noise is always present, and in a fundamental sense it can never be completely eliminated. In any case, Shannon proceeded to abstracting and making precise the notion of noise. The details are rather technical, and can be found in Shannon's original paper or, in a more accessible language, in The Shannon-Weaver Model, already referenced above.

   

  

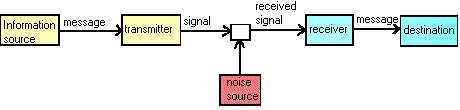
  Shannon's General Model of Communication

   

  Shannon's paper was not merely a theoretical masterpiece. The simplicity of the communication model illustrated above perhaps hides its profound practical implications. Read Wyner's The Significance of Shannon's Work The Shannon-Weaver Model,
• Another fundamental milestone was the invention by J Bardeen, W Brattain and W Shockley in 1947 (they were awarded the 1956 Nobel Prize in physics), of the transistor, which replaced the vacuum tube in computers, as well as in radio, and later in television sets. Relative to the vacuum tube, the transistor's size (less than 1/10), power consumption (about 1/20), reliability and cost resulted in a dramatic acceleration of the development of more and more powerful computers. The first machines to make full use of transistor technology were the early supercomputers: Stretch by IBM and LARC by Sperry-Rand. This fundamental invention in turn made possible many subsequent improvements. For example, in 1958 Jack Kilby and Noyce developed the integrated circuit (IC), a single silicon chip, on which several computer components could be fitted. This was followed by large scale integration (LSI), very large scale integration (VLSI), and ultra-large scale integration (ULSI). These technologies squeezed first hundreds, then thousands, and ultimately millions of components onto one chip. Read an interesting account by Ronald Kessler, Absent at the Creation; How One Scientist Made off with the Biggest Invention Since the Light Bulb.
  Here is a simple illustration of the operation of a transistor.

   

  

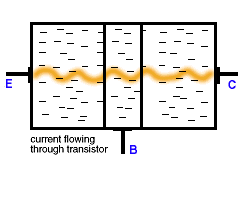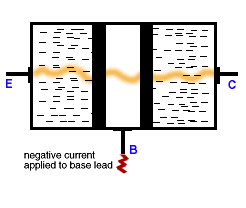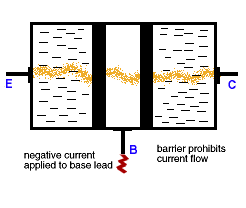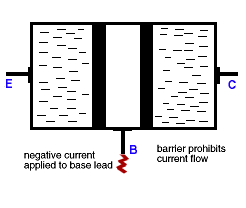
  The Transistor Effect

   

  "This animation shows the transistor effect as the transistor is made to alter its state from a starting condition of conductivity (switched 'on', full current flow) to a final condition of insulation (switched 'off', no current flow).
  The animation begins with current flowing through the transistor from the emitter (point E) to the collector (point C). When a negative voltage is applied to the base (point B), electrons in the base region are pushed ('like' charges repel, in this case both negative) back creating insulation boundaries. The current flow from point E to point C stops. The transistor's state has been changed from a conductor to an insulator." [ from Lucent Technologies's Transistor: What is It? ]
• According to Williams [ op. cit., p. 301 ]

  "probably the most important aspect of the development of modern computers was the production of devices to serve as memory systems for the machines. From the earliest days of the construction of the stored program computer, the main memory design was the controlling factor in determining the rest of the machine architecture. It was certainly the case that the construction of large reliable storage devices was one of the syumbling blocks in the creation of the early machines.

  It was recognized very early on that a computer's memory should have a number of properties:

  • it must be possible to erase the contents of the memory and store new data in place of the old;
  • it must be possible to store information for long periods of time;
  • it must be inexpensive to construct because it would be needed in large quantities;
  • it must be possible to get at the information being stored in very short periods of time…;

  None of the early devices was able to completely satisfy all of these requirements; but magnetic core memory came as close as any. It should be noted that it was only from about 1975, when large-scale integrated circuits became available, that memory systems satisfying all these requirements were produced."

• I will therefore limit myself here to describing the magnetic core memory.

   

  

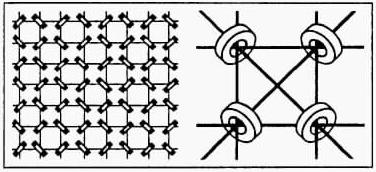
  Schematic Illustration of the Magnetic Core Memory

   

   

  

  Closeup of an Actual Section of Magnetic Core Memory

   

  Each tiny magnetic 'doughnuts' or ring can be magnetized in such a way that its magnetic field points along either direction perpendicular to the plane of the ring. This direction can thus be interpreted as storing 1 bit of information (two choices). 'Writing' such a bit was accomplished by two of the wires (called the 'X and Y wires'), and 'reading' it was the function of the third wire (called the 'sense wire'). Core memories were non-volatile. Among the first machines to employ them were MIT's Whirlwind, and the UNIVAC. The credit for their invention goes to several people, and in particular to J Forrester, D Buch, J Rajchman and A Wang. Magnetic core memories "remained in use for many years in mission-critical and high-reliability applications. The Apollo Guidance Computer, for example used core memory, as did the Space Shuttle until a recent computer upgrade."
  [ from Project History: Magnetic Core Memory ]

 
Readings, Resources and Questions

• Read another short biography of Claude Elwood Shannon and visit the beautiful and informative site on Information Theory at Lucent Technologies.
• Here are a few references to the most important machines built in the late '40s and early '50s.
  A good description of The Manchester Machine (1948-1950) can be found at the The Alan Turing Internet Scrapbook site.
  Martin Campbell-Kelly not only describes the EDSAC (1949), "the world's first stored-program computer to operate a regular computing service," but offers The Edsac Simulator. "intended for use in teaching the history of computing."
  Besides being involved with the design of the Manchester Machine, Alan Turing participated in the construction of the Automatic Computing Engine (ACE) (1950) at the National Physical Laboratory, London. Visit also  The Turing Archive for the History of Computing.
  Princeton University's Institute of Advanced Studies IAS General Purpose Computer is often considered "the first computer designed as a general purpose system with stored instructions. Von Neumann helped design the system, and most computers of the next 30 years or so were referred to as 'Von Neumann machines' because they followed the principles he built into this system."
  The UNIVAC I (Universal Automatic Computer) began to operate at the US Census Bureau in 1951. It "was used to predict the 1952 presidential election. Noone believed its prediction, based on 1% vote in, that Eisenhower would sweep the election. He did."

  The Whirlwind computer (1951) was designed by a team led by Jay Forrester, and "was the first digital computer capable of displaying real time text and graphics on a video terminal, which at this time was a large oscilloscope screen. The Whirlwind was also the first computer to use Core Memory for RAM."

• Visit the Transistor Museum.