MacKenzie, I. S., & Buxton, W. (1994). The prediction of pointing and dragging times in graphical user interfaces. Interacting with Computers, 6, 213-227. [PDF] [software]

The Prediction of Pointing and Dragging Times in Graphical User Interfaces

I. Scott MacKenzie1 and William Buxton2

1Dept. of Computing & Information Science
University of Guelph
Guelph, Ontario
Canada N1G 2W1

2Computer Systems Research Institute
University of Toronto
Toronto, Ontario
Canada M5S 1A4

Abstract
An experiment is described demonstrating that the point-drag sequence common on interactive systems can be modeled as two separate Fitts' law tasks – a point-select task followed by a drag-select task. Strong prediction models were built; however, comparisons with previous models were not as close as the standard error coefficients implied. Caution is therefore warranted in follow-up applications of models built in research settings. Additionally, the previous claim that "target height" is the appropriate substitute for target width in calculating Fitts' index of difficulty in dragging tasks was not supported. The experiment described herein varied the dragging target's width and height independently. Models using the horizontal width of the drag target or the smaller of the target's width or height outperformed the target height model.

Keywords: interaction techniques, pointing and dragging tasks, Fitts' law, human performance modeling

INTRODUCTION

The graphical user interface, popularized in 1983 with the introduction of the Apple Macintosh, has redefined the way humans interact with computers. Present-day mouse-driven interfaces employ sophisticated yet natural techniques for user input. "Pointing", "dragging", "inking", etc., form the core repertoire of interaction techniques in graphical user interfaces.

This paper presents and critiques prediction models for the common tasks of pointing and dragging. Our aim is (a) to illustrate the potential benefits and problems in using Fitts' law models as an engineer's approximate model as per Card, Moran, and Newell's (1983) Model Human Processor, and (b) to establish which target dimension is the most appropriate "target width" for pointing and dragging tasks on a 2D CRT display. We will present models from past research, describe an experiment building new models, and compare and reconcile the differences between these models.

Just as language is a tool for thought, models are tools for organizing and articulating ideas for the researcher or designer. One such model that captures the common acts of pointing and dragging in interactive systems is the Three-State Model for Graphical Input (Buxton, 1990). Pointing is represented as a State 1 action and dragging as a State 2 action (see Figure 1). Selection is a brief transition from State 1 to State 2 and back again via a mouse button. (State 0 actions are the "out-of-range" motions possible with a mouse or stylus while airborne.) The three-state model forms a vocabulary for exploring relationships – affordances or constraints – between input devices and interactive techniques.


Figure 1. Simple two-state interaction. In State 1, mouse motion moves the tracking symbol. Pressing and releasing the mouse button over an icon selects the icon and leaves the user in State 1. Depressing the mouse button over an icon and moving the mouse drags the icon. This is a State 2 action. Releasing the mouse button returns to the pointing state. From Buxton (1990).
The three-state model is descriptive. As a predictive model we call upon Fitts' law, an information processing model for human motor-sensory behaviour (Fitts, 1954). Prediction models are important for HCI since they allow interface scenarios to be explored a priori. Performance measures can be estimated "on paper" with choices formed early in the design process. The presence of Fitts' law as one of nine principles of operation in Card, Moran, and Newell's (1983) Model Human Processor has inspired substantial use of the law by HCI researchers.

Although Fitts' law has surfaced extensively as a prediction model for pointing tasks, its application to dragging tasks is limited to the studies by Gillan, Holden, Adam, Rudisill, and Magee (1990, 1992) and MacKenzie, Sellen, and Buxton (1991). We will review these following a brief introduction to Fitts' law. For extensive reviews, see MacKenzie (1992), Meyer, Smith, Kornblum, Abrams, and Wright (1990), or Welford (1968).

Fitts' Law

According to Fitts (1954), a movement tasks' index of difficulty (ID) can be quantified using information theory by the metric "bits". Specifically,

ID = log2(2A / W) (1)

where A is the distance or amplitude to move and W is the width or tolerance of the region within which the move terminates. From Equation 1, the time to complete a movement task is predicted as

MT = a + b ID (2)

where a and b are the intercept and slope coefficients from linear regression.

Variations of Fitts' law have surfaced to correct systematic biases in regression analyses. These include the Welford (1968) formulation:

MT = a + b log2(A / W + 0.5) (3)
and the Shannon formulation (MacKenzie, 1989):

MT = a + b log2(A / W + 1) (4)

Equation 4 is preferred because it

(a) provides a slightly better fit with observations,
(b) exactly mimics the information theorem underlying Fitts' law, and
(c) always gives a positive rating for ID.

Extension to Two Dimensions

The experiments undertaken by Fitts and most other experimental psychologists tested one dimensional movements. HCI researchers generally use target selection tasks on a two-dimensional CRT display. The shape of the target and the angle of approach, therefore, must be considered in applying the model. For rectangular targets, we still view the amplitude as the distance to the target's centre, but the definition of target width is unclear. This is illustrated in Figure 2.


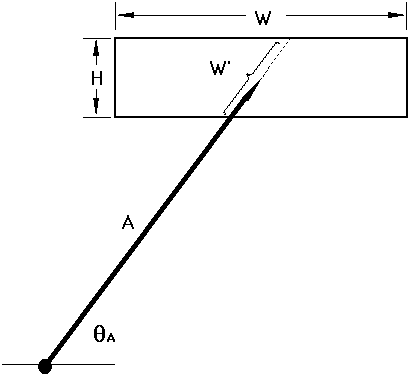
Figure 2. The two-dimensional problem: What is target width? Possibilities include the horizontal extent of the target (the STATUS QUO model), the smaller of the target's width or height (the SMALLER-OF model), or the length of the target along the approach axis (the W' model).

For 2D tasks, the question arises: What is target width? The default strategy is to consistently use the horizontal extent of the target. We call this the "STATUS QUO" model for target width. Unfortunately, a STATUS QUO model yields unrealistically low (sometimes negative!) estimates for task difficulty when, for example, a short and wide target such as a word approached from above or below at close range. At least two examples of this exist in the literature (see MacKenzie, 1992).

We suggest two ways to correct this. The first is to use the Shannon formulation for ID, which always yields a positive rating for ID. A second and additional strategy is to substitute for W a measure more consistent with the 2D nature of the task. In Figure 2 the inherent 1D nature of the model is maintained by measuring W along the approach axis. Shown as W' in the figure, we call this the "W' model". The W' model is appealing because it allows a 1D interpretation of a 2D task, thus maintaining the theoretical premise of the law.

Another possible substitution for target width is "the smaller of W or H". This pragmatic approach has intuitive appeal in that the smaller of the two dimensions seems more indicative of the accuracy demands of the task. We call this the "SMALLER-OF" model.

We conducted an experiment to test the different models for target width on a standard 2D target selection task using a mouse (MacKenzie and Buxton, 1992). The design employed a balanced range of short-and-wide and tall-and-narrow targets approached from various angles. The results indicated that both the SMALLER-OF and W' models are empirically superior to the STATUS QUO model and that the difference between the SMALLER-OF and W' models is insignificant. The model with the highest correlation was

MT = 230 + 166 log2(A / W + 1) (5)

where W equaled the smaller of W or H (SMALLER-OF model). Equation 5 had a correlation of r = .950 and a standard error of estimate of SE = 63 ms. The latter measure is important in establishing confidence intervals for subsequent applications of Fitts' law models as engineering tools.

For further evidence, we need only examine the observations of Gillan et al. (1990, 1992), who used conditions of W = 0.25, 1.0, 3.5, and 6.0 cm with H held constant at 0.5 cm (the height of a character). The targets were words or phrases of length 1, 5, 14, or 26 characters. The observed selection time decreased from the 1-character to the 5-character conditions for each amplitude condition (as expected for both models); however, MT remained the same across the 5-, 14-, and 26-character conditions. The latter effect, although not accounted for by the STATUS QUO model, is fully expected with the SMALLER-OF model because target height was constant and consistently smaller than target width.

The Point-Drag Sequence

An important task in graphical user interfaces is the point-drag sequence. This is illustrated in Figure 3 for the common action of selecting a block of text.


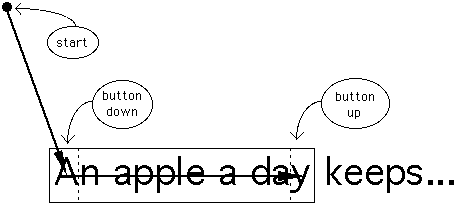
Figure 3. The point-drag sequence. The task has two components: a point-select task ending with the button-down action, and a drag-select task ending with a button-up action.

Selecting the phrase "An apple a day" requires, first, a point operation (State 1) terminating with a button-down action on the letter "A", and second, a drag operation (State 2). The drag operation is a motion through the block of text with the button held down, terminating in the region of the last character in the block. We consider this two separate Fitts' law tasks, a point sequence followed immediately by a drag sequence. For each component of the move, the width of the target (W) should be modeled using the SMALLER-OF or W' models, as described earlier. In both cases, the rectangular region containing a single character is the target.

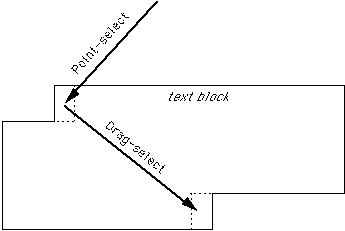
If the angles of movement change or if the text block covers several lines, the approach angles (and W') change somewhat, but the two-dimensional extensions discussed above still apply (Figure 4). The model is applied exactly the same for other point-drag sequences, such as pull-down menus or scroll bars.


Figure 4. The point-drag sequence in two dimensions. For the point-select and drag-select tasks, the target is the region containing a single character.
Fitts' Law in Dragging Tasks

The studies by Gillan et al. (1990, 1992) and MacKenzie et al. (1991) are the only existing applications of Fitts' law to dragging tasks. Gillan et al. (1990, 1992) tested Fitts' law in point-select and point-drag-select tasks. They concluded that "dragging time in a point-drag sequence is under control of two features of a computer display: the dragging distance and the height of the text object" (1990, p. 232). Two models were compared: one substituting the constant 0.5 cm for target width and another substituting target height, H. A higher correlation was found in the latter case, and this led to the conclusion above. We are suspicious of the "target height" model because character width was positively correlated with character height. It is felt that Gillan et al. (1990) inadvertently confirmed the strength of the STATUS QUO model for one-dimensional tasks. In a subsequent paper, they concluded that "dragging time was affected by both dragging distance and the font size of the text object" (1992, p. 306). This is a more reasonable conclusion, however it is not generalizable to dragging tasks with arbitrary targets such as scroll bars or menus.

In the only other test of Fitts' law in dragging tasks, MacKenzie et al. (1991) tested serial pointing and dragging and found a slightly less efficient rate of information processing during dragging than during pointing (3.0 bits/s vs. 4.2 bits/s). A serial task similar to Fitts (1954) was employed, so the models of are restricted practical use. However, since dragging immediately follows pointing in the point-drag sequence, the serial dragging model may be appropriate in this limited case. The mouse-dragging model was

MT = 135 + 249 log2(A / W + 1) (6)

with r = .992 and SE = 38 ms. Equation 6 for dragging, and the pointing model presented earlier (Equation 5), will be tested later against the models from the experiment described in the next section.

METHOD

In this section we describe an experiment using a point-select (State 1) task followed by a drag-select (State 2) task. It is claimed that the effect is that of two Fitts' law tasks in sequence. Two prediction equations should apply, reflecting the inherent information processing capacities in each task.

Subjects

Twelve male students from a local college volunteered as subjects and were paid an hourly rate. All subjects used computers on a daily basis.

Apparatus

An Apple Macintosh II microcomputer served as the host computer with input through a standard mouse. The output display was a 33 cm colour CRT monitor (used in black-and-white mode) with a resolution of 640 by 480 pixels.

Procedure

Subjects performed multiple trials of a simple point-drag-select task. The task was demonstrated prior to starting and a block of warm-up trials was administered prior to data collection.

For each trial, a small circle appeared near the centre of the CRT display, and a target, in the form of a horizontal scroll bar, appeared elsewhere (see Figure 5). Subjects were instructed to manipulate the mouse to move the cursor inside the circle, then wait for a visual cue before beginning. The cue was a small black rectangular bar which appeared on the left of the screen (see Figure 5) and slowly expanded in size for about 1 second. After the bar stabilized, a move could begin. Subjects could take as long as necessary to prepare for each move, but were told to move as quickly and accurately as possible once the cursor left the circle. The graduating cue prevented them from treating the experiment as a reaction time task as its end point, the start signal, was not well defined.

Timing began when the cursor left the circle. The task was a point-select action followed immediately by a drag-select action. For the point-select action, subjects acquired the left rectangle in the horizontal bar (at the top in Figure 5). For the drag-select action subjects dragged the rectangle horizontally and deposited it in the right rectangle. The procedure resembled the operation of a horizontal scroll bar on the Macintosh though no scrolling resulted.

The point-select task was timed from the cursor leaving to the start circle to the button-down action in the left rectangle of the horizontal bar. The drag-select task was timed from the button-down action terminating the point-select task to the button-up action where the rectangle was dropped on the right. A pointing error was recorded if the button-down action was outside the left rectangle. A dragging error occurred if the two rectangles did not overlap when the button-up action occurred.


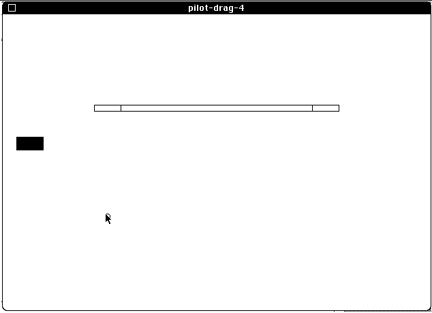
Figure 5. The experimental task. Subjects began by positioning the cursor inside the small circle. The point-select sequence terminated with a button-down action in the left rectangle. The drag-select sequence terminated with a button-up sequence in the right rectangle after dragging across the horizontal bar. The left rectangle moved with the cursor during the drag operation.
If a move started before the bar stabilized, a beep was heard and the subject had to reposition the cursor inside the circle and restart the move.

Design

A fully within-subjects repeated measures design was used. Controlled variables were approach angle (θA = 0°, 45°, & 90°), point amplitude (A1 = 2, 4, 8, 16, & 32 units), drag amplitude (A2 = 2, 4, 8, 16, & 32 units), target width (W = 1, 2, 4, & 8 units), and target height (H = 2 & 4 units). Each experiment unit equaled 10 pixels. The greatest horizontal distance covered was 480 pixels (8.0 cm), corresponding to A1 = 16 units, A2 = 32 units, and θA = 0°. Dependent variables were movement time (MT) and error rate. Measurements were taken separately for the pointing and dragging components of each move. Movement time for the initial point operation (MTP) was timed from the cursor leaving the start circle to the button-down action at the pick-up region on the left of the target (see Figure 5). Movement time for dragging (MTD) was timed from the end of the point operation to the button-up action at the drop region on the right.

Only 102 of 600 possible cells were used to keep the experiment manageable and to exhaust a wide and relevant range of test conditions. Thirty-four distance/size conditions (see Table 1) were crossed with the three approach angles. Drag amplitudes were selected in power-of-four increments starting at 2 × W. This provided at least W units of separation between the pick-up and drop regions for dragging.

Table 1
Distance/Size Conditions Used in Experiment
Width Height Point Amplitudea Drag Amplitudea Combinations
 2   4   8  16 32  2   4   8  16 32
1 2 x . x . x x . x . . 6
2 2 x . x . x . x . x . 6
4 2 . x . x . . . x . x 4
8 2 . . x . x . . . x . 2
1 4 . x . x . x . x . x 6
2 4 . x . x . . x . x . 4
4 4 . x . x . . . x . x 4
8 4 . . x . x . . . x . 2
Total: 34
a x = used; . = not used (Note: point and drag conditions crossed)

The 102 conditions were presented in random order until all conditions were exhausted. This constituted one block. A total of 15 blocks were administered over four days for a total of 1530 trials per subject.

RESULTS AND DISCUSSION

The mean time to complete moves was 633 ms (SD = 213 ms) for the pointing phase of tasks followed by 827 ms (SD = 226 ms) for the dragging phase. Mean error rates were 1.8% (SD = 3.7%) for pointing and 4.2% (SD = 6.0%) for dragging.

Although 102 unique conditions were tested (see Table 1), the data were aggregated by conditions unique to each of the pointing and dragging phases of the tasks. Aggregating by point-amplitude, width, height, and angle left 54 conditions for the pointing analysis. Aggregating by drag-amplitude, width, and height left 15 conditions for the dragging analysis. Regressing MTP (ms) on ID, where ID = log2(A / SOWH + 1), yielded

MTP = 177 + 169 ID (7)

with r = .9637 (p < .001) and SE = 54 ms.[1] Regressing MTD (ms) on ID, where ID = log2(A / W + 1), yielded

MTD = 345 + 198 ID (8)

with r = .9711 (p < .001) and SE = 54 ms. The high correlations in these analyses are, in themselves, support for the hypothesis that point-drag-select tasks can be modeled as two separate Fitts' law tasks, each with its own prediction equation.

Fitts' Law Models as Engineering Tools

A goal of this experiment was to take prediction equations built in previous research and test their potential as engineering tools to predict subsequent behaviour in a different setting. Accordingly, the prediction equations and standard error of estimates from previous models for pointing (MacKenzie & Buxton, 1992, Equation 5) and dragging (MacKenzie et al., 1991, Equation 6) are compared with the equations from the present experiment.

A scatter plot of points is shown in Figure 6 for pointing and in Figure 7 for dragging. Each point plotted was derived from the mean of more than 300 observations. The dashed lines apply to the present experiment, with the range of conditions delimited on the left and right, and the 95% confidence intervals (on observed points) delimited on the top and bottom. The solid lines show the 95% confidence intervals predicted from the earlier models.


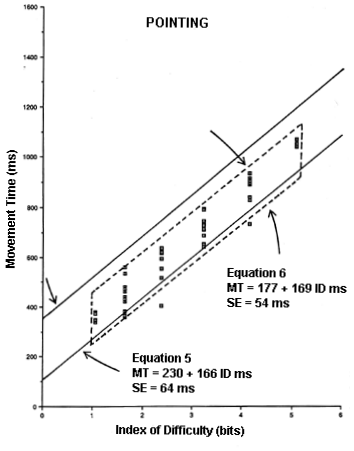
Figure 6. Model comparison for the point-select sequence. The scatter plot and dashed lines are for the current experiment (Equation 7). The solid lines delimit the 95% confidence intervals from a previous experiment (Equation 5).

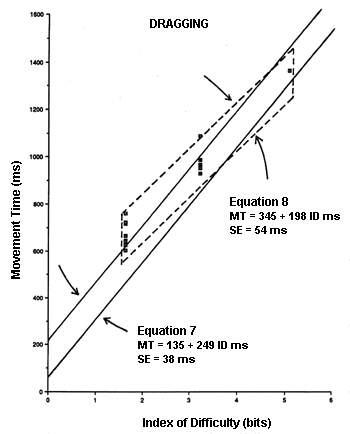
Figure 7. Model comparison for the drag-select sequence. The scatter plot and dashed lines are for the current experiment (Equation 8). The solid lines delimit the 95% confidence intervals from a previous experiment (Equation 6).
Of the 54 aggregate points for pointing, four (8.9%) were below the predicted 95% confidence band from Equation 5; none was above. Of the 15 aggregate points for dragging, eight (53.3%) were above the predicted 95% confidence band from Equation 6; none was below.

The use of a model derived from a serial dragging task (Equation 6) may be inappropriate for the dragging phase of a discrete point-drag-select task. It is evident in Figure 7 that Equations 6 and 8 have very different intercepts and slopes. The regression coefficients and standard errors (SEs) for the predictions equations and for each regression coefficient are summarized in Table 2 for the four equations in question.

Table 2
Comparison of Four Regression Coefficients
Equation ra SE
(ms) 		Regression Coefficients
Intercept,
a (ms) 		SE
(ms) 		Slope,
b (ms/bit) 		SE
(ms) 		IP
(bits/s)b
*** Pointing ***
5 .9501 64 230 21 166 6.2 6.0
6 .9637 54 177 19 169 6.5 5.9
*** Dragging ***
7 .9921 38 135 36 198 13.0 5.1
8 .9711 54 345 36 198 13.0 5.1
a p < .001
b IP = 1/b

Since the correlations were very high (r > .9000, p < .001), it is not surprising that standard errors throughout were low. It appears the regression equations were all highly representative of observations in the respective tasks. More relevant, however, is whether or not the two pointing equations are "the same", and whether or not the two dragging equations are "the same". The standard error for each regression coefficient is valuable for this comparison. First, examining the two pointing equations with Equation 7 as the reference, the slope coefficients only differ by (169 - 166) / 6.5 = 0.46 SEs. The intercept in Equation 5, however, is 2.8 SEs higher than the intercept in Equation 7. The latter difference would only occur 0.5% of the time through random effects (with the assumption of normality); so, despite the insignificant differences in slopes, it cannot be assumed that the two prediction equations apply to the same underlying task. This may be attributable to the subtle differences in the tasks (point-select vs. point-drag-select).

The two dragging equations in Table 2 are quite different. Using Equation 8 as the reference, the slope is 3.9 SEs higher and the intercept 5.8 SEs lower for Equation 6. There are several possible sources of this disparity. First, the models are from experiments conducted separately using different subjects. Second, the range of conditions was different. IDs ranged from 1 to 6 bits in MacKenzie et al. (1991) and from 1.8 to 5 bits in the present experiment. Finally, the tasks were different. Equation 8 was derived from a serial dragging task, but was applied to data for the dragging phase of a discrete point-drag-select task.

We expect even greater disparities if the derived models were applied to State 1 and State 2 actions in real applications on interactive graphics systems, where an assortment of user actions arise. Tasks such as selecting words or blocks of text in a word processing environment, acquiring and manipulating icons, or selecting an item in a pull-down menu would severely test the generality of a model built in a research environment. As engineering tools, designers are cautioned not to rely on establish Fitts' law models to provide accurate predictions unless the device and task conditions in the new interface closely match those from the original research.

Target Width in Dragging Tasks

Since the present experiment included a balanced set of square, short-and-wide, and tall-and-narrow drag targets (see Table 1), H and W were not correlated. This permitted a valid test of Gillan et al.'s (1990) model against the STATUS QUO and SMALLER-OF models. (The W' model is the same as the STATUS QUO model, in this case, because the approach angle was consistently 0°.)

Correlations for the STATUS QUO, SMALLER-OF, and target height models respectively were .9711 (p < .001), .9688 (p < .001), and .6403 (p < .005). The poor showing of the target height model was fully anticipated. Since target height is measured perpendicular to the line of approach (in left-to-right dragging tasks), there is no reasonable basis for it to serve as target width in the model. Target height would have only a slight effect on movement time, since motion was one-dimensional along the horizontal axis. Therefore, the top ranking for the STATUS QUO model (which is the same as the W' model in this case) was not surprising.

CONCLUSION

This paper has demonstrated that the point-drag sequence common on interactive systems with a graphical user interface can be modeled as two separate Fitts' law tasks – a point-select task followed by a drag-select task. Prediction models with high correlations and low standard errors were developed; however, when compared with models from previous research using similar tasks, the predictions were not as close as the standard errors implied. Based on this, we conclude that caution must be exercised in taking models built in a research setting and applying them subsequently on real systems: A model with a very high correlation may not stand-up to subsequent predictions in different settings.

The present attempt to apply derived models to subsequent tasks illustrates the difficulty in adopting models such as Fitts' law to practical problems in interface design. Meeting the usual statistical tests for validity seems easy in comparison to the challenges in applying the model later. Expectations must be kept low. A statistically sound model will be accompanied by a small standard error of estimate; but confidence intervals will not be met later unless the model was derived under conditions very similar to the application.

A problem in applying Fitts' law in two dimensional tasks is in choosing an appropriate "target width" to substitute as "W" in the calculation of task difficulty. The claim of Gillan et al. (1990) that target height is the appropriate substitute for target width in dragging tasks was not supported. The experiment described herein varied the dragging target's width and height independently. Both the STATUS QUO model and the SMALLER-OF model outperformed the target height model. We conclude that the appropriate substitute for target width in two-dimensional pointing or dragging tasks is either the smaller of the target's width or height (SMALLER-OF model), or the width of the target along the angle of approach (W' model).

ACKNOWLEDGEMENTS

This research was supported by the Natural Sciences and Engineering Research Council of Canada, Xerox Palo Alto Research Center, Digital Equipment Corp., and Apple Computer Inc. We gratefully acknowledge this contribution, without which, this work would not have been possible.

REFERENCES

Boritz, J., Booth, K. S., & Cowan, W. B. (1991). Fitts's law studies of directional mouse movement. Proceedings of Graphics Interface '91, 216-223. Toronto, Ontario: Canadian Information Processing Society.

Buxton, W. (1990). A three-state model of graphical input. In D. Diaper et al. (Eds.), Human-Computer Interaction - INTERACT '90, 449-456. Amsterdam: Elsevier.

Card, S. K., Moran, T. P., & Newell, A. (1983). The psychology of human-computer interaction. Hillsdale, NJ: Erlbaum.

Fitts, P. M. (1954). The information capacity of the human motor system in controlling the amplitude of movement. Journal of Experimental Psychology, 47, 381-391.

Fitts, P. M., & Peterson, J. R. (1964). Information capacity of discrete motor responses. Journal of Experimental Psychology, 67, 103-112.

Gillan, D. J., Holden, K., Adam, S., Rudisill, M., & Magee, L. (1990). How does Fitts' law fit pointing and dragging? Proceedings of the CHI '90 Conference on Human Factors in Computing Systems, 227-234. New York: ACM.

Gillan, D. J., Holden, K., Adam, S., Rudisill, M., & Magee, L. (1992). How should Fitts' law be applied to human-computer interaction. Interacting with Computers, 4, 291-313.

MacKenzie, I. S. (1989). A note on the information-theoretic basis for Fitts' law. Journal of Motor Behavior, 21, 323-330.

MacKenzie, I. S. (1992). Fitts' law as a research and design tool in human-computer interaction. Human-Computer Interaction, 7, 91-139.

MacKenzie, I. S., & Buxton, W. (1992). Extending Fitts' law to two-dimensional tasks. Proceedings of the CHI '92 Conference on Human Factors in Computing Systems, 219-226. New York: ACM.

MacKenzie, I. S., Sellen, A., & Buxton, W. (1992). A comparison of input devices in elemental pointing and dragging tasks. Proceedings of the CHI '91 Conference on Human Factors and Computing Systems, 161-166. New York: ACM.

Meyer, D. E., Smith, J. E. K., Kornblum, S., Abrams, R. A., & Wright, C. E. (1990). Speed-accuracy operating tradeoffs in aimed movements: Toward a theory of rapid voluntary action. In M. Jeannerod (Ed.), Attention and performance XIII (pp. 173-226). Hillsdale, NJ: Erlbaum.

Welford, A. T. (1968). Fundamentals of skill. London: Methuen.