Silfverberg, M., MacKenzie, I. S., & Korhonen, P. (2000). Predicting text entry speed on mobile phones. Proceedings of the ACM Conference on Human Factors in Computing Systems - CHI 2000, pp. 9-16. New York: ACM.
Predicting Text Entry Speed on Mobile Phones
Miika Silfverberg1, I. Scott MacKenzie2, and Panu Korhonen1
1Nokia Research CenterP.O. Box 407
FIN-00045 Nokia Group
Finland
+358 40 528 7759
{miika.silfverberg | panu.korhonen}@nokia.com
2Dept. of Mathematics & Statistics
York University
Toronto, Ontario
Canada M3J 1P3
+1 416 736 2100
smackenzie@acm.org
Abstract
We present a model for predicting expert text entry rates for several input methods on a 12-key mobile phone keypad. The model includes a movement component based on Fitts' law and a linguistic component based on digraph, or letter-pair, probabilities. Predictions are provided for one-handed thumb and two-handed index finger input. For the traditional multi-press method or the lesser-used two-key method, predicted expert rates vary from about 21 to 27 words per minute (wpm). The relatively new T9 method works with a disambiguating algorithm and inputs each character with a single key press. Predicted expert rates vary from 41 wpm for one-handed thumb input to 46 wpm for two-handed index finger input. These figures are degraded somewhat depending on the user's strategy in coping with less-than-perfect disambiguation. Analyses of these strategies are presented.Keywords: Text entry, mobile systems, mobile phones, keypad input, human performance modeling, Fitts' law, digraph frequencies
INTRODUCTION
Designing new text entry methods for computing systems is labour intensive. It is also expensive, since a working prototype must be built, and then tested with real users. Because most text entry methods take time to learn, the testing should preferably take place in longitudinal settings. However, longitudinal user studies are tedious [13]. A pragmatic approach is to develop a predictive model to "test" new text entry methods a priori — without building prototypes or training users. Models, at their best, can be valuable and informative tools for designers of new text entry methods [1, 13].
This research is concerned with the problem of text entry on mobile phones. Although we usually think of phones as devices for speech input and output, the transmission and reception of text messages on mobile phones is increasing rapidly. For example, Finland's largest teleoperator, Sonera, reports a six-fold increase of text messages during 1998 (http://www.sonera.fi/investor_en/publications/annualreports/sonera98_english.pdf).
Text entry on contemporary mobile phones is mainly based on the 12-key keypad (Figure 1). This paper describes a method for predicting potential expert user text entry speed for input methods that utilize the 12-key keypad. The model provides individual predictions for one-handed thumb and two-handed index finger use.

Figure 1. The 12-key keypad
State of the Art of Text Entry on Mobile Phones
The 12-key keypad consists of number keys 0-9 and two additional keys (# and *). Characters A-Z are spread over keys 2-9 in alphabetic order. The placement of characters is similar in most mobile phones, as it is based on an international standard [8]. The placement of the SPACE character varies among phones. In this paper, we assume the 0-key serves as the SPACE character.Since there are fewer keys than the 26 needed for the characters A-Z, three or four characters are grouped on each key. Thus, ambiguity arises. For example, if the user presses key 2, the system must determine which of the characters A, B, or C the user intends. There are several approaches to this problem. We present three: the multi-press, the two-key, and the T9 methods.
Multi-press Input Method
The multi-press method is currently the main text input method for mobile phones. In this approach, the user presses each key one or more times to specify the input character. For example, the number key 2 is pressed once for the character 'A', twice for 'B', and three times for 'C'.The multi-press approach brings out the problem of segmentation. When a character is placed in the same key as the previously entered character (e.g., the word on), the system must determine whether the new key press still "belongs to" the previous character or represents a new character.
Therefore, a mechanism is required to specify the start of a new character. There are two main solutions to this. One is to use a timeout period within which key presses belong to same character. Most phones have a timeout, typically between 1 and 2 seconds. The other solution is to have a special key to skip the timeout ("timeout kill") thus allowing the next character — on the same key — to be entered directly. Some phone models use a combination of the two solutions. For example, Nokia phones include both a 1.5-second timeout and the provision for a timeout kill using the arrow keys. The user may decide which strategy to use. We provide predictions for both.
Two-key Input Method
In the two-key method, the user presses two keys successively to specify a character. The first key press, as in the multi-press method, selects the "group" of characters (e.g., key 5 for 'JKL'). The second press is for disambiguation: one of the number keys, 1, 2, 3, or 4, is pressed to specify the position of the character within the group. For example to enter the character 'K', the user presses 5-2 ('K' is second character in 'JKL').The two-key method is very simple. There are no timeouts or such. Each character A-Z is entered with exactly two key presses. SPACE is entered with a single press of the 0-key.
The two-key method is not in common use for entering Roman characters, however. In Japan, a similar method (often called the "pager" input method) is very common for entering Katakana characters.
T9 Input Method
A third way to overcome the problem of ambiguity is to add linguistic knowledge to the system. The T9 input method, patented by Tegic Communications, Inc. (Seattle, WA) [8], uses a dictionary as the basis for disambiguation. The method is based on the same key layout as the multi-press method, but each key is pressed only once. For example, to enter "the", the user enters the key sequence 8-4-3-0. The 0-key, for SPACE, delimits words and terminates disambiguation of the preceding keys. T9 compares the word possibilities to its linguistic database to "guess" the intended word.Naturally, linguistic disambiguation is not perfect, since multiple words may have the same key sequence. In these cases, T9 gives the most common word as a default. To select an alternate word, the user presses a special NEXT function key. For example, the key sequence 6-6 gives "on" by default. If another word was intended, the user presses * to view the next possible word. In this case, "no" appears. If there are more alternatives, NEXT (*) is pressed repeatedly until the intended word appears. Pressing 0 accepts the word and inserts a SPACE character.
Based on our informal analyses, disambiguating works quite well. In a sample of the 9025 most common words in English (ftp://ftp.itri.bton.ac.uk/) produced from the British National Corpus, the user must press NEXT only after about 3% of the words. Naturally, the whole vocabulary is larger than 9025 words, so this estimate may be optimistic. However, 5% is a reasonable approximation, and will be used throughout this paper.
Most major mobile phone manufacturers have licensed the T9 input method, and, as of 1999, it has surfaced in commercial products (e.g., the Mitsubishi MA125, the Motorola i1000Plus, the Nokia 7110 ). There is also a touch-screen version of T9 that is available for PDAs (e.g., the Palm Computing Palm III, the Philips Nino ). Bohan et al. [2], describe an evaluation of the touch screen version; however, to our knowledge, there are no published evaluations of T9 with physical keys.
MODEL FOR MOBILE PHONE TEXT ENTRY
Our model is similar to that of Soukoreff and MacKenzie [15]. It is based on two components: a movement model (Fitts' law) and a linguistic model (digraph probabilities).
Movement Model (Fitts' Law)
The core of this paper is the application of Fitts' law to the mobile phone keypad. Fitts' law [6] is a quantitative model for rapid, aimed movements. It can be used to calculate the potential text entry speed of an expert user, assuming that the text entry performance of an expert is highly over-learned, and thus is limited only by motor performance. We will elaborate more on this assumption later.Fitts' law has been applied with success to pointing devices [5, 12] and on-screen keyboards [13, 14]. There are only a few studies, however, that apply Fitts' law to physical keyboards. Card et al. [3] suggested using Fitts' law for keying times on a calculator. Drury and Hoffmann [4] used Fitts' law to evaluate the performance tradeoffs of various inter-key gaps for data entry keyboards. Fitts' law is expressed as
| MT = a + b log2(A/W + 1) | (1) |
where A is the length (amplitude) of a movement, and W is target size (width), in this case, the size of the pressed key [10]. Fitts' law is inherently one-dimensional, as evidenced by a single "width" term. Physical keys on a mobile phone keypad, however, are laid out in a two-dimensional array, and each key has both width and height. Therefore, we need to extend the model to two dimensions. For this purpose we substitute for W in Equation 1 the smaller of the width and height, as suggested by MacKenzie and Buxton [11]. In most cases, height is less than the width for keys of a mobile phone. Therefore, we used the height of the keys as W.
The log term in Equation 1 is called the index of difficulty (ID ):
| MT = a + b × ID | (2) |
The two constants, a and b, are determined empirically by regressing observed movement times on the index of difficulty. For this purpose, we collected empirical data from both one-handed thumb use (Experiment 1, see below) and two-handed index finger use (Experiment 2).
In mobile phone text entry, each character is entered with one or more key presses, i.e., movements. The first of these, the initial movement, M0, consists of moving the finger over the desired key (e.g., key 'ABC' for character 'a') and pressing the key. Depending on the input method, there may be none, one or several additional movements (M1, M2, etc.).
For each movement (M0, M1, M2, etc.), Fitts' law is used to predict the movement time (MT0, MT1, MT2, etc.). The total time to enter a character, CT, is calculated as the sum of all the required movements:
| CTij = S MTk | (3) |
The details, of course, depend on the text entry method. Below, we explain the models for each of the three text entry methods.
Movement Model for Multi-press Input Method
In the multi-press method, the user presses each key one or several times. There are two strategies, varying in their treatment of the timeout. We model these separately.If the user allows the built-in timeout to segment consecutive characters on the same key, the character entry time is calculated as follows:
| CT = MT0 + N × MTrepeat + Ttimeout | (4) |
MT0 is the initial movement time, i.e., the time to move one's finger or thumb from the first key of the digraph to the second key. N is the number of key repetitions, which is an integer from 0 to 3 depending on character (e.g., character 'C' requires two extra presses of key 'ABC', N = 2). MTrepeat is the key-repetition time, which equals the intercept a in the Fitts' law equation (ID = 0).
For Ttimeout, we used 1.5 seconds. This is the time used in Nokia phones, although it may vary among manufacturers. Ttimeout is required only if the second character, j, is on the same key as the first character, i.
Alternatively, the user may explicitly override the timeout by pressing a timeout kill key (the down-arrow key in Nokia phones). In the latter case, the character entry time is
| CT = MT0 + N × MTrepeat + MTkill | (5) |
where MTkill is the time to move to the arrow key.
Movement Model for Two-Key Input Method
In the two-key method, each character except SPACE requires two key presses. Therefore, character entry time is simply calculated as a sum of two movement times:
| CT = MT0 + MT1 | (6) |
With the SPACE character, the second movement time is zero.
Movement Model for T9 Input Method
In the T9 input method, each key is pressed only once. Also, there is no timeout. Therefore, the character entry time is simply calculated as:
| CT = MT0 | (7) |
This model for T9 is for perfect disambiguation, and assumes the NEXT function is not needed. We will discuss the implications of this in detail later.
Linguistic Model (Digraph Probabilities)
Our linguistic model uses a 27 × 27 matrix of letter-pair (digraph) frequencies in common English [15]. The 27 characters include the letters A-Z and the SPACE character.Each letter-pair, i-j, is given a probability Pij based on an analysis of representative sample of common English. The sum of all probabilities is one:
| Σ Σ Pij = 1 | (8) |
Since our predictions are based on a linguistic model, they are inherently language-specific, applying only to common English. However, because the language model is simple, the results are easy to adapt to another language by changing the digraph probabilities according to that language.
Combining the Models
To develop predictions we need to combine the motor and linguistic models. An average character entry time for the language (CTL ) is calculated as a weighted average of character entry times for all digraphs:
| CTL = S S (Pij × CTij ) | (9) |
Taking the reciprocal of CTL gives us the average number of characters per second, which can be transformed into words per minute by multiplying by 60 seconds per minutes and dividing by 5 characters per word:
| WPM = (1 / CTL ) × (60 / 5) | (10) |
METHOD
Our model is still incomplete, since the coefficients a and b in the Fitts' law equations are unknown for finger input on a 12-key phone keypad. Two experiments were carried out to determine these coefficients. Experiments 1 and 2 described below sought to determine these for one-handed thumb input and two-handed index finger input, respectively.
Experiment 1: One-handed Thumb Input
In this experiment participants held the phone in a preferred hand and pressed the keys with the thumb of the same hand. The other (non-preferred) hand was held idle.
Participants
Twelve volunteers (7 male, 5 female) participated in the study. Most participants were employees of the Nokia Research Center in Helsinki. Their ages ranged from 24 to 47 years, with an average of 32.6 years.Five of the participants were left-handed; however, two choose to hold the phone with their right hand. The right-handed participants held the phone in their right hand. All participants had prior experience in using a 12-key phone keypad. Ten participants were regular mobile phone users. The average mobile phone experience of all participants was 3.9 years.
Apparatus
The number keypad of a Nokia 5110 mobile phone was used as the model 12-key keypad (Figure 3). Only the number keys (1-9) and * and # keys were used in the experiment. Number keys are slightly larger than * and # keys. The dimensions are shown in Figure 2. As mentioned previously, the height of keys was used in calculating ID. Key dimensions and distances between keys were measured using a slide gauge.
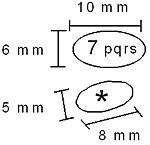 Figure 2
|
 Figure 3 |
Test Tasks
The participant's task was to press specified keys on the phone keypad for a period of 10 seconds at a time. Participants were instructed to press the keys as fast as they could but to avoid errors.There were two types of tasks:
- Single keys: In these tasks the participants pressed only a single key. There were four key repeat tasks altogether (keys 1, 3, 7 and 9).
- Key pairs: In these tasks the participants pressed two keys alternately for 10 seconds. A subset of all possible pairs of keys was chosen to cover a range of movements, for example, from very short (e.g., key 1 - key 4) to very long (e.g., key 3 - key *). The inter-key distances ranged from 9 to 38 mm, with an average of 20.6 mm. The key pairs were selected to create similar movements for left- and right-handed participants.
Procedure
The tasks were presented to participants in random order. The "write messages" function of the phone (with number mode selected) was enabled during the tasks; thus, the phone automatically showed the number of written characters. A 10-second countdown timer controlled the task time (except for the first three participants, whose time was controlled manually with a stopwatch). The test moderator signaled the start of each task by saying "1-2-3-go" and pressing the start key on the countdown timer. After 10 seconds, the countdown timer gave a clearly audible sound. The participants were instructed to stop pressing the keys when they heard this sound. Key presses entered after the stop signal were ignored. The test moderator checked the number of key presses from the phone's display and recorded it in a spreadsheet file. The average movement time (in milliseconds) between successive key presses was then calculated using formula:
| MT = 10000 / (N - 1) | (11) |
where N is the number of key presses during a 10 second interval. Error data were not collected.
Experiment 2: Two-handed Index Finger Input
Experiment 2 was similar to Experiment 1 except the index finger was used instead of the thumb. Users held the phone in one hand and entered key presses with the index finger of the other hand.
Participants
Twelve volunteers (7 male, 5 female) participated in the study. Seven had also participated in Experiment 1. Ages ranged from 23 to 41 years, with an average of 29.8 years.Five of the participants were left-handed. One, however, choose to press keys with the right hand. The right-handed participants used their right hand. All participants had some experience using a standard phone keypad. Eleven were regular mobile phone users. The average mobile phone experience of all participants was 4.0 years.
RESULTS
Figure 4 shows the results from Experiment 1 and 2. In both experiments, the movement time (MT ) grows linearly with index of difficulty (ID ), as predicted by Fitts' law.
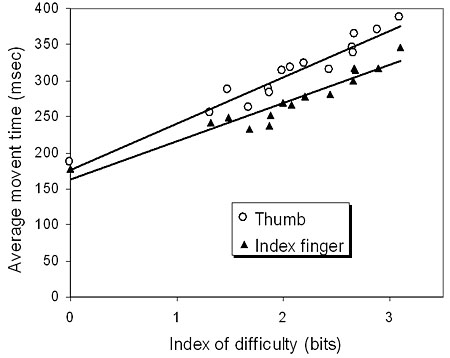
Figure 4. Results from Experiments 1 and 2
A linear regression of MT on ID was performed. The results are given in Figure 5.
| Mode | Intercept, a (ms) | Slope, b (ms/bit) | Correlation |
|---|---|---|---|
| Index finger | 165 | 52 | .960 |
| Thumb | 176 | 64 | .970 |
The correlations in the linear regression are high, indicating that Fitts' law predicts the movement time with high accuracy both with the index finger and thumb.
Overall, the index finger was faster than the thumb. The average movement time between successive key presses in all conditions was 273 ms for the index finger, and 309 ms for the thumb.
The analysis of variance of movement time showed clear main effects for both index of difficulty (F13,692 = 85.9, p < .0001) and input finger (F1,692 = 114.1, p < .0001). The ID-by-finger interaction was not significant (F13,692 = 1.7, p > .05).
The two points with ID = 0 are substantially to the left of the other points, and this is a concern. Although it has been suggested that Fitts' law does not apply when ID is small [7], a more legitimate explanation lies in the treatment of spatial variability in building the model. Fitts' law is predicated upon the assumptions that (a) the spatial distribution of end-points is normal and (b) 4% of the distribution falls outside the target region. Where possible, it is desirable to use IDe computed from We and Ae — the actual, or "effective", amplitude and width of the distributions. We could not do so in this simple experiment because there was no means to capture end-points. However, if We and Ae could have been used, then clearly the task with ID = 0 would have We > 0 and Ae > 0, and, hence, IDe > 0. This would tend to shift the points at ID = 0 to the right [10].
Model Predictions for Mobile Phone Text Input
Based on Experiments 1 and 2, the movement time on mobile phone keypad can be reliably predicted using Fitts' law equations:
| MTindex finger = 165 + 52 log2( A / W + 1) ms | (12) |
and
| MTthumb = 176 + 64 log2( A / W + 1) ms | (13) |
Incorporating this information, our model gives predictions of potential expert user text entry speeds. The results are shown in Figure 6.
| Method | Index finger | Thumb |
|---|---|---|
| Multi-press - wait for timeout - timeout kill |
22.5 27.2 |
20.8 24.5 |
| Two-key | 25.0 | 22.2 |
| T9 | 45.7 | 40.6 |
Two predictions are given for the multi-press method corresponding to the two possible interaction strategies. If consecutive characters are on the same key, the user may either wait for the timeout to pass, or end it manually. In our model, the timeout was 1.5 seconds. Our model predicts that with this timeout, "timeout kill" is clearly the faster strategy (21% faster when using the index finger, 18% with the thumb). It is assumed that expert users adopt the faster strategy. This is supported by our observations of users at the Nokia Research Center: a majority of experienced multi-press users employ the timeout kill strategy.
Predictions are clearly higher for the T9 method than for the multi-press and two-key methods. These differences, and other interaction issues for T9, are discussed in detail later.
In comparing the multi-press and two-key methods, the multi-press method is slower if the user employs the timeout strategy — waiting for the timeout between consecutive characters on the same key. However, as expertise develops, users will invoke the timeout kill function. With an optimal use of timeout kill, the multi-press method is faster than the two-key method.
Input via the index finger is also consistently faster than with the thumb. The difference is largest with T9 and the two-key input methods where the index finger is 13% faster than with the thumb. The difference is smaller with the multi-press method. This is due to the steeper slope of the Fitts' law model for the thumb in Figure 4. With small IDs the difference between the index finger and thumb is quite small; the multi-press method involves many key repetitions (ID = 0), which diminishes the difference between the index finger and thumb.
Within the multi-press method, the difference for the index finger is larger with the "timeout kill" strategy (11%) than with "wait for timeout" (8%). This is due to the constant length of the timeout, which diminishes the differences between input fingers in our "wait for timeout" results.
Comparisons With Empirical Data
There are, at present, no published data on text entry rates with mobile phones. As this mode of interaction evolves and enters the mainstream of mobile computing, however, this should change. Furthermore, there are few people who may be deemed "experts" in mobile phone text entry. The investigation described herein is in anticipation of an ever-increasing demand for this mode of text entry.While formal user studies are preferred, we commonly perform quick and simple checks of novel text entry techniques using the well-known phrase, "the quick brown fox jumps over the lazy dog". This 43-character phrase includes every letter of the alphabet, and therefore ensures that each key, or key combination, is visited during entry.
Within our lab, one user performs a substantial amount of mobile phone text entry via the multi-press method, and, in our view, approaches the status of expert. For example, this person routinely uses the timeout kill feature where applicable. We asked this person to perform timed input of the quick-brown-fox phrase. In three repetitions using thumb input, the times were 27 s, 23 s, and 24 s, with 0 errors in each case. The mean entry time was 24.6 s. For a 43-character phrase, this translates into a text entry rate of 21.0 wpm. This is surprisingly close to our predicted expert entry rate of 24.5 wpm.
We asked the same user to perform the same test with a T9-enabled cell phone. We asked the user to ignore the possible need for the NEXT function, and to enter the phrase directly. The entry times were 15 s, 15 s, and 16 s. The only error was for the key sequence 5-2-9-9-0, which T9 incorrectly disambiguated to "jazz" instead of "lazy". The mean entry time of 15.7 s translates into an entry rate of 32.9 wpm. Keeping in mind that this user does not use T9 on a daily basis, the observed rate is reasonably close to our predicted expert entry rate of 40.6 wpm.
Interaction and Linguistic Issues for T9
The very generous predictions for T9 in Figure 6 should be viewed in the narrow context of our model. For example, our model is for experts and ignores the novice or learning behaviour that most users of this emerging input technique will experience.As well, our model attends only to the motor component of the interaction. The need to visually scan the keyboard to find each character is not accounted for. We feel this is a relatively minor issue, since most users are already familiar with phone keypads. Expert status, in the sense of knowing the position of characters on a phone keypad, should be easily acquired in our view.
Of greater concern is the role of the NEXT function with T9. Two questions arise. First, how often is the NEXT function required? And second, what behaviour will users exhibit in using the NEXT function?
The answer to the first question is determined by the dictionary, or linguistic model, embedded in T9. It is relatively straightforward to determine the outcome of disambiguation for any dictionary. For example, Figure 7 provides an analysis using the word sample discussed earlier. The results are quite impressive. Of the 9025 words in the sample, 8437 (95%) can be entered and uniquely disambiguated.
The number of words requiring 1, 2, 3, 4, or 5 presses of the NEXT function is 476, 83, 23, 5, and 1, respectively.
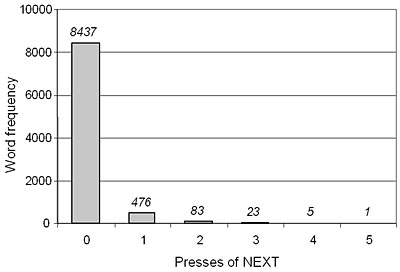
Figure 7. Use of NEXT for a sample of 9025 words
Figure 8 illustrates some ambiguous words - those requiring 4 or 5 presses of the NEXT function.
| Key sequence | Initial word | Presses of NEXT | Subsequent words |
|---|---|---|---|
| 2-2-7-3 | case | 5 | care, base, card, bare, cape |
| 2-6-9 | any | 4 | boy, box, cow, box |
| 7-2-4-3 | said | 4 | page, paid, raid, rage |
| 7-2-6 | ran | 4 | sam, san, pan, ram |
| 7-2-9 | say | 4 | saw, pay, raw, ray |
The initial word for any key sequence is the one with the highest probability in the linguistic model, while subsequent words are produced in decreasing order of their probability. Note that our word sample, as well as that in the T9 dictionary, includes proper nouns (e.g., Sam).
Although the T9 dictionary and the disambiguation process are considered proprietary by Tegic, we tested a T9-enabled mobile phone with the key sequences in Figure 8. All the words in Figure 8 were produced, although there were a few minor differences in the sequences.
Answering the second question above is much more difficult since it involves user strategies. Although as many as 95% of words entered will correctly appear by default, users will not necessarily anticipate this. Thus, there is a need for the user to visually verify input. This behaviour is outside the scope of our model, as noted earlier. It is also a behaviour that is difficult to empirically model, since there are both perceptual and cognitive processes at work.
Figure 9 presents a parametric analysis of the use of the NEXT function for two components of the behaviour for thumb input. First, the percentage of words for which visual inspection is performed is included: 0%, 25%, 50%, 75%, and 100%. For the 0% condition, the user never visually verifies input. For the 100% condition, the user visually verifies input after each word entered.
Second, the perceptual-plus-cognitive time associated with visual inspection is shown along the horizontal axis as a continuum from 0 to 1000 ms. Note that the movement time for multiple invocations of the NEXT function is quite small because it requires multiple presses of the same key (*).
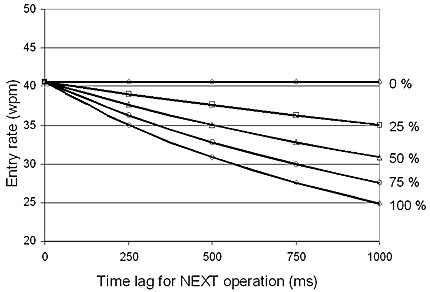
Figure 9. Parametric analysis for T9 user behaviour (see text for discussion)
Expert usage appears along the top line in Figure 9. That is, the user always knows when the next function is required and never visually verifies input. Although this behaviour will never fully occur, it may occur by degree. For example, a user may quickly learn that the word "on" requires the key sequence 6-6-0, whereas the word "no" requires the NEXT function: 6-6-*-0.
If the user visually verifies input 50% of the time (far more often than necessary, in fact), and each inspection takes 500 ms, then the T9 prediction falls to 35 wpm (see Figure 9). Bear in mind that this prediction is still predicated upon expert behaviour with respect to the keypad layout (i.e., no visual scan time to find the correct key). So, the prediction is still overly generous, perhaps.
Exploring hypothetical scenarios such as this, although important in characterizing user behaviour, is very weak in its ability to generate accurate predictions. Modeling expert performance is a luxury that affords a simplified view of user behaviour. Once we step off this ideal and attempt to accommodate more natural components of the interaction, there is an explosion in the sources and extent of variations. And so, the preceding exploration of T9 interaction will not be developed further. Suffice it to say that we expect T9 text entry rates to be slower than those cited above, consistent with a user's position on the learning curve and on the interaction strategy employed.
There are many other interactions issues, as well, such as the need to input numeric and punctuation symbols, or words not in the dictionary. Implementations of T9 we have tested include modes to insert words using the multi-press technique or to insert symbols from a displayed list. These important properties of the interaction are not accounted for in our current model.
CONCLUSIONS
We have provided predictions for expert text entry rates for several input schemes on mobile phones. The traditional multi-press method can support rates up to about 25 wpm or 27 wpm for one-handed thumb input or two-handed index finger input, respectively, provided the user effectively employs the timeout kill feature for consecutive characters on the same key. If the timeout is used to distinguish consecutive characters on the same key, then the entry rates will decrease by about 4 wpm in each case.The two-key input technique is slightly slower than the multi-press method (using timeout kill): 22 wpm and 25 wpm for one-handed thumb input and two-handed index finger input, respectively.
The relatively new T9 technique requires only one key press per character, and relies on a built-in linguistic model to disambiguate input on a word-by-word basis. Text entry rates of 41 wpm and 46 wpm are predicted for one-handed thumb input and two-handed index finger input, respectively. These figures are for expert behaviour and a "perfect" disambiguation algorithm. Our analyses suggest that word-level disambiguation for English text with the traditional character layout on phone keypad is achievable with about 95% accuracy. The overhead of interacting with less-than-perfect disambiguation degrades performance, but the cost is difficult to quantify because of the complex and varied strategies that users may employ.
REFERENCES
[1] Bellman, T., and MacKenzie, I. S. A probabilistic character layout strategy for mobile text entry, In Proceedings of Graphics Interface '98. Toronto: Canadian Information Processing Society, 1998, pp. 168-176.[2] Bohan, M., Phipps, C. A., Chaparro, A., and Halcomb, C. G. A psychophysical comparison of two stylus-driven soft keyboards, In Proceedings of Graphics Interface '99. Toronto: Canadian Information Processing Society, 1999.
[3] Card, S. K., Moran, T. P., and Newell, A. The psychology of human-computer interaction, (Hillsdale, NJ: Lawrence Erlbaum, 1983).
[4] Drury, C. G., and Hoffmann, E. R. A model for movement time on data-entry keyboards, Ergonomics 35 (1992), 129-147.
[5] Epps, B. W. Comparison of six cursor control devices based on Fitts' law models, In Proceedings of the Human Factors Society--30th Annual Meeting. Santa Monica, CA: Human Factors Society, 1986, pp. 327-331.
[6] Fitts, P. M. The information capacity of the human motor system in controlling the amplitude of movement, Journal of Experimental Psychology 47 (1954), 381-391.
[7] Gan, K.-C., and Hoffmann, E. R. Geometrical conditions for ballistic and visually controlled movements, Ergonomics 31 (1988), 829-839.
[8] Grover, D. L., King, M. T., and Kuschler, C. A. Patent No. US5818437, Reduced keyboard disambiguating computer. Tegic Communications, Inc., Seattle, WA (1998).
[9] ISO/IEC 9995-8: 1994: Information systems - Keyboard layouts for text and office systems - Part 8: Allocation of letters to the keys of a numeric keypad, International Organisation for Standardisation, 1994.
[10] MacKenzie, I. S. Fitts' law as a research and design tool in human-computer interaction, Human-Computer Interaction 7 (1992), 91-139.
[11] MacKenzie, I. S., and Buxton, W. Extending Fitts' law to two-dimensional tasks, In Proceedings of the CHI '92 Conference on Human Factors in Computing Systems. New York: ACM, 1992, pp. 219-226.
[12] MacKenzie, I. S., Sellen, A., and Buxton, W. A comparison of input devices in elemental pointing and dragging tasks, In Proceedings of the ACM Conference on Human Factors in Computing Systems - CHI '91. New York: ACM, 1991, pp. 161- 166.
[13] MacKenzie, I. S., and Zhang, S. The design and evaluation of a high-performance soft keyboard, In Proceedings of the ACM Conference on Human Factors in Computing Systems - CHI '99. New York: ACM, 1999, pp. 25-31.
[14] Martin, G. L. Configuring a numeric keypad for a touch screen, Ergonomics 31 (1988), 945-953.
[15] Soukoreff, W., and MacKenzie, I. S. Theoretical upper and lower bounds on typing speeds using a stylus and keyboard, Behaviour & Information Technology 14 (1995), 370-379.