Soukoreff, R. W., & MacKenzie, I. S. (2003). Metrics for text entry research: An evaluation of MSD and KSPC, and a new unified error metric. Proceedings of the ACM Conference on Human Factors in Computing Systems - CHI 2003, pp. 113-120. New York: ACM.
Metrics for Text Entry Research:
An Evaluation of
MSD and KSPC, and a New Unified Error Metric
R. William Soukoreff1 and I. Scott MacKenzie1,2
1 Department of Computer ScienceYork University
Toronto, Ontario, Canada, M3J 1P3
{will, smackenzie}@acm.org
2 Unit for Computer-Human Interaction (TAUCHI)
Dept. of Computer & Information Sciences
FIN-33014 University of Tampere
Tampere, Finland
ABSTRACT
We describe and identify shortcomings in two statistics recently introduced to measure accuracy in text entry evaluations: the minimum string distance (MSD) error rate and keystrokes per character (KSPC). To overcome the weaknesses, a new framework for error analysis is developed and demonstrated. It combines the analysis of the presented text, input stream (keystrokes), and transcribed text. New statistics include a unified total error rate, combining two constituent error rates: the corrected error rate (errors committed but corrected) and the not corrected error rate (errors left in the transcribed text). The framework includes other measures including error correction efficiency, participant conscientiousness, utilised bandwidth, and wasted bandwidth. A text entry study demonstrating the new methodology is described.
INTRODUCTION
The introduction of computers and word processors has changed text entry forever. In the past, using typewriters, speed was measured with a stopwatch and errors were tallied by hand. Technology has changed this. Today, document preparation is less about dictating text sent to the typing pool, and more about using a word-processor as an composition aid. This change has left the term "error rate" ill-defined and difficult to measure.
Facing the problem of calculating text entry error rates, we discovered an algorithm well known in some areas of computer science, but, to our knowledge, without previous application in text entry [7]. The algorithm and accompanying analysis technique involve two statistics: the minimum string distance error rate (MSD error rate) and keystrokes per character (KSPC).
The primary weakness of the analysis technique is the lack of a single error rate metric combining the desirable features of both statistics. A combined metric is both psychologically and theoretically desirable, but a means to combine the existing metrics has so far been elusive. In view of this, we devised a novel analysis framework that generates the two previous error metrics and that gives rise to a new combined error rate.
We begin with an introduction to error rate analysis in text entry studies. Next, the new framework and combined error rate metric are described. Finally, the new methodology is used to analyse the results of a study.
ERROR RATE ANALYSIS IN TEXT ENTRY STUDIES
Ubiquitous computing and mobile text messaging are driving the search for efficient text entry technologies for mobile devices. Novel methods are evaluated in controlled experiments where humans enter text while speed and accuracy are observed. Measuring speed is relatively easy; however, this is not true of error rate. Consider the following example:
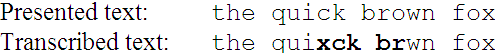
A character-wise comparison suggests that six errors were committed (indicated in boldface), although two errors seems more likely: an extra 'x' was typed, and an 'o' was omitted. Although character-wise comparisons are easy to implement in software, the result is problematic, as just demonstrated. Two pragmatic solutions used in previous research are to preclude errors (i.e., the user must correctly enter each character before proceeding, [1]) or to force users to maintain synchronicity with the presented text (so error analysis degenerates to a simple pair-wise comparison of characters, [5]). Both of these procedures are unnatural, compromising the external validity of the experiment.
Recently we proposed a methodology for measuring error rates using the minimum string distance (MSD) and keystrokes per character (KSPC) statistics [7]. There are two advantages of the technique:
- Participants are allowed to enter text naturally. They may commit errors and make corrections, unencumbered by artificial experimental procedures.
- The identification of errors and generation of error rate statistics is easy to automate, without requiring tedious manual tabulation.
Minimum String Distance Error Rate
Text entry experiments generate pairs of strings: presented text (what participants were asked to enter) paired with transcribed text (what was actually entered). The minimum string distance (MSD) between the strings is the minimum number of primitives — insertions, deletions, or substitutions — to transform one string into the other. (Pseudo-code of an MSD algorithm is provided in [7].) The MSD statistic represents the number of errors committed by the user while entering the presented text. The MSD error rate is a simple extension of the MSD statistic:
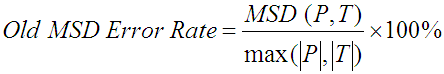
| (1) |
where P and T are the presented and transcribed text strings, and the vertical bars,
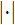 , represent the length of the strings. Using the maximum
length of the two strings in the denominator ensures (a) the error rate upper limit is
100%, (b) undue credit is not given if the user enters less text than presented, and
(c) an appropriate penalty is exacted if the user enters more text than presented.
, represent the length of the strings. Using the maximum
length of the two strings in the denominator ensures (a) the error rate upper limit is
100%, (b) undue credit is not given if the user enters less text than presented, and
(c) an appropriate penalty is exacted if the user enters more text than presented.
Equation 1 is the original formulation of the MSD error rate [7]. In further work, we found that the MSD error rate (as given above) was occasionally wrong when analysing the specific errors committed [4]. In view of this, we introduced a slight correction to the MSD error rate formula. The correction reconciles the disparity in lengths of the alignments (in essence, ASCII representations of the differences between the presented and transcribed text strings). For a given presented-transcribed text pair, there may be multiple alignments, comprising a set of possible explanations of the erroneous behaviour. This set of alignment strings was used to formulate a new MSD error rate:
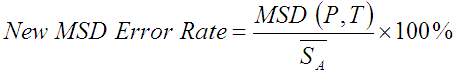
| (2) |
where
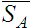 is the mean length of the alignment strings in the set. Equation 2 is heretofore
preferred because it always yields the same error rate as that obtained by a
character-by-character analysis of errors. In practice, Equation 2 yields a value
similar to but less than Equation 1, because
is the mean length of the alignment strings in the set. Equation 2 is heretofore
preferred because it always yields the same error rate as that obtained by a
character-by-character analysis of errors. In practice, Equation 2 yields a value
similar to but less than Equation 1, because
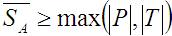 .
.
Key Strokes Per Character (KSPC)
The natural experimental procedure afforded by introducing the MSD error rate produces an interesting side effect. Now, there are two classes of errors: those not corrected (the MSD error rate measures these), and those that are corrected. The latter do not appear in the transcribed text. Previously we noted that the KSPC statistic captures this second class of errors [7].1
Consider this example:
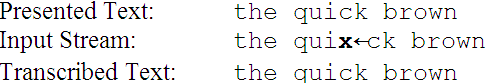
The user entered an incorrect character ('x') that was deleted with a backspace
('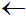 '). These keystrokes do not appear in the transcribed text,
hence the transcribed text is error free and the MSD error rate is 0%. Clearly, the
MSD error rate is not telling the whole story.
KSPC is defined as
'). These keystrokes do not appear in the transcribed text,
hence the transcribed text is error free and the MSD error rate is 0%. Clearly, the
MSD error rate is not telling the whole story.
KSPC is defined as
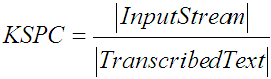 . .
| (3) |
Assuming a regular keyboard was used for the-quick-brown example above, the
input stream contains 17 keystrokes (including 'x' and
' '),
and the transcribed text contains 15 characters. So there were 17 / 15 = 1.13
keystrokes per character. If the text was entered without errors, KSPC would be 1.00.
In general, the more errors and corrections made, the higher the resulting KSPC.
'),
and the transcribed text contains 15 characters. So there were 17 / 15 = 1.13
keystrokes per character. If the text was entered without errors, KSPC would be 1.00.
In general, the more errors and corrections made, the higher the resulting KSPC.
KSPC is a useful characteristic of text input methods. For example, error-free typing on a Qwerty keyboard averages around 1.0 KSPC because each keystroke generates one character, whereas entering text using multi-tap2 on a mobile phone requires 2.03 KSPC on average [2]. However, as we now demonstrate, the utility of KSPC to capture the overhead of correcting errors is less than ideal. There are three shortcomings of KSPC that limit its utility as an error metric:
- KSPC measures a combination of two interesting quantities, without providing a means to separate them. KSPC is interpreted as the cost of committing errors and fixing them. A large KSPC value indicates that many errors were committed and correction was easy (took few keystrokes) or that few errors were committed but correcting them was arduous (requiring many keystrokes). However, KSPC does not distinguish between these two opposing conditions.
- KSPC depends on the text input method under study. As noted, error-free typing results in a different KSPC for a Qwerty keyboard than for multi-tap on a mobile phone. So a study comparing the error rates or efficiency of error correction of these two text input methods cannot meaningfully compare their KSPC values. For example, a user committing few errors with multi-tap would still have about twice the KSPC value as an error-prone user using a Qwerty keyboard.
- Although there is an inverse relationship between the KSPC and MSD, there is no
obvious way to combine them in an over-all error rate. The-quick-brown example
above yielded a 0% MSD error rate and 1.13 KSPC. However, if the user did not notice
the mistake and made no correction, the input stream would contain 16 keystrokes (i.e.,
no
'
 ') and the transcribed text would contain 16 characters (the
erroneous 'x' remains). Hence, by not correcting the error, the MSD error rate rises
to 6.25%, while KSPC falls to 1.0. Clearly an inverse relationship exists:
participants can shift errors back-and-forth between the MSD error rate and KSPC by
investing more or less effort in error correction. It is desirable to have a single
error rate metric combining both error rates.
') and the transcribed text would contain 16 characters (the
erroneous 'x' remains). Hence, by not correcting the error, the MSD error rate rises
to 6.25%, while KSPC falls to 1.0. Clearly an inverse relationship exists:
participants can shift errors back-and-forth between the MSD error rate and KSPC by
investing more or less effort in error correction. It is desirable to have a single
error rate metric combining both error rates.
DECONSTRUCTING THE TEXT INPUT PROCESS
The example above illustrates that there is more information in the input stream than in the transcribed text. It is by analysing the classes of keystrokes in the input stream that a new perspective of error rate arises.
Constituents of the Input Stream
Our earlier observation that users produce transcribed text while entering presented text is an over-simplification. In reality, users produce an input stream that when processed by a text-box widget, command line, or word processor, is converted into the transcribed text. Within the input stream are keystrokes (some correct, some erroneous) and editing commands (backspace, delete, cursor movements, etc.). Figure 1 divides the keystrokes of the input stream into four classes, depending upon how they affect the error rate.

Figure 1 - Constituents of the input stream
Correct keystrokes correspond to the Correct (C) sector of Figure 1. Errors unnoticed by the typist and hence remaining in the transcribed text correspond to the Incorrect and Not Fixed (INF)3 sector. Together, these two classes of keystrokes (not shaded in Figure 1) comprise all of the characters in the transcribed text.
Figure 1 has two shaded sectors. These represent keystrokes in the input stream that are not present in the transcribed text. Errors corrected correspond to the Incorrect but Fixed (IF) sector, and keystrokes performing the corrections comprise the Fixes (F) area. F keystrokes annihilate IF keystrokes, and hence neither are present in the transcribed text. Given the presented text, input stream, and transcribed text, it is straightforward to classify keystrokes with the preceding taxonomy.
C & INF All characters in the transcribed text belong to the C or INF classes. The INF keystrokes are identifiable with the MSD function. The C keystrokes are the correct characters in the transcribed text. F Keystrokes belonging to the F class are easy to identify because they are editing functions. Examples include backspace, delete, cursor movement, as well as modifier keys (shift, alt, and control) when used in conjunction with these editing functions. IF The IF keystrokes are those in the input stream, but not in the transcribed text, that are not editing keys.
Given this taxonomy, it is clear that classifying keystrokes is not difficult, and can be relegated to software. Finding the particular characters in each class affords a more detailed analysis of errors on a character-by-character basis [4]. However, in computing error rates, the particular characters do not interest us. Instead it is the size of the classes that is important. Therefore, as a notational convenience let C, INF, IF, and F, denote the number of keystrokes in each of their respective classes.4 It is now possible to define analogues of the MSD error rate and KSPC statistic in terms of the keystroke taxonomy,
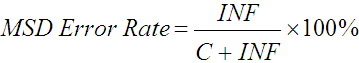 , and , and
| (4) |
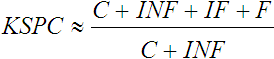 . .
| (5) |
An Example
Consider how the keystrokes of the following example map into the classes above.
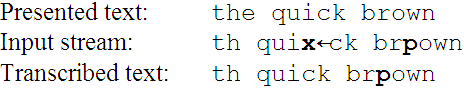
In this example there are three errors: an 'e' is omitted, there is an extra 'x' that is corrected with a backspace, and there is an extra 'p' that remains uncorrected. These keystrokes are mapped into the keystroke taxonomy in Figure 2.
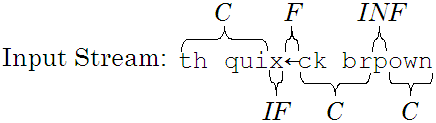
Figure 2 - Classifying the keystrokes in an example
One detail missing in Figure 2 is that the INF class also includes the missing 'e' keystroke. In this example, C = 14, INF = 2 (counting the extra 'p', and the missing 'e'), IF = 1, and F = 1.
Table 1 compares the formulations for MSD error rate and KSPC discussed so far. As noted, the old and new formulations of MSD do not always yield identical results, but they are comparable in value. Note also that the formulation of KSPC based on the keystroke taxonomy does not yield an identical value to the usual definition of KSPC, although it is very close in value. This difference arises because the INF class includes characters that were omitted from the transcribed text (like 'e' in the example); if there were no omitted characters, then the two KSPC values are identical.
Comparison of Error Statistics
| Statistic | Eq. | Value |
|---|---|---|
| Old MSD error rate | 1 | 13.3 % |
| New MSD error rate | 2 | 12.5 % |
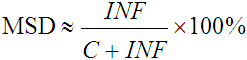
| 4 | 12.5 % |
| KSPC | 3 | 1.13 |
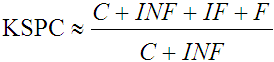
| 5 | 1.125 |
The keystroke taxonomy yields expressions that, while not necessarily identical to the MSD error rate and KSPC statistic, are essentially equivalent. Next we consider what new statistics and insights are possible with the taxonomy.
NEW METRICS ARISING FROM THE TAXONOMY
The first shortcoming of KSPC listed earlier is the inability to separate corrected errors from fixes. With the taxonomy, this is trivial. The taxonomy tells us the number of errors made and corrected (IF), the number of errors made but not corrected (INF), the total number of errors (INF + IF), and the number of keystrokes invested in error correction (F). The keystroke taxonomy will, as described in the next section, allow us to formulate the combined (total) error rate. First, however, we present a few other interesting statistics now available. Error correction efficiency refers to the ease with which the participant performed error corrections. It is defined as
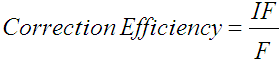 . .
| (6) |
Using the IF and F values from the previous example, IF / F = 1 / 1 = 1. In other words, fixing the error took about the same effort as creating the error in the first place. This result arises only because the error was noticed and fixed immediately by the typist, and because the keyboard provides an efficient means to correct the error (the backspace key). Typical behaviour, however, is not always so efficient. Consider the input stream when an error is noticed two or three words behind the cursor position. We may see repeated cursor-left keystrokes, some correction keystrokes, and perhaps a cursor-end keystroke to reposition the cursor to where it began. In this case the error correction efficiency will be less than one. On the other hand, if whole words, lines, or paragraphs must be deleted, one could hold down the shift and control keys while pressing the cursor keys, to select large blocks of text. It is possible to perform a large correction with only a few keystrokes resulting in an efficiency greater than one. Correction efficiency is most useful when taken as an average over many trials.
Another statistic of interest is participant conscientiousness, expressed
 . .
| (7) |
Participant conscientiousness represents the ratio of corrected errors to the total number of errors. In the example, IF / (IF + INF) = 1 / (1 + 2) = 1/3, indicating that the participant caught and fixed one third of their errors. This statistic provides a means to distinguish perfectionists from apathetic participants. If text entry is viewed as information transfer, then C represents the amount of useful information transferred, and INF, IF, and F represent wasted bandwidth.5 The proportion of bandwidth representing useful information transfer is
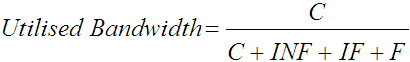 , ,
| (8) |
and the proportion of wasted bandwidth is
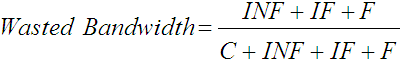 . .
| (9) |
The above statistics provide a convenient overall picture of the efficiency of the strategies and behaviours of a participant. Calculating means of these statistics provides a characterisation of the overall efficiency of a text entry method.
Total Error Rate
In the preceding section we demonstrated how the taxonomy provides many useful statistics for the text entry investigator. The taxonomy also provides an intuitive definition of total error rate:
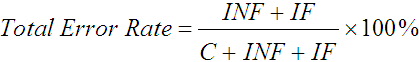 . .
| (10) |
If no errors are made, then INF and IF are both zero, resulting in a zero total error rate. If errors are made, they result in the same error rate regardless of whether they were corrected or not. Putting effort into correcting errors, transfers keystrokes from INF to IF, but does not affect the total error rate. In the previous example the total error rate would be (INF + IF) / (C + INF + IF) = 3 / 17 = 17.6%.
Conveniently, the formulation above naturally splits into corrected and not corrected error rates:
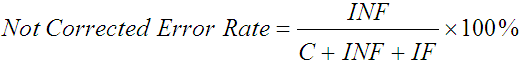 , ,
| (11) |
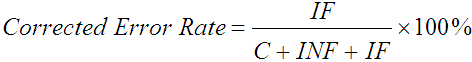 , ,
| (12) |
with the property that Not Corrected Error Rate + Corrected Error Rate = Total Error Rate. Using values from the previous example, the Not Corrected Error Rate = INF / (C + INF + IF) = 2 / (14 + 2 + 1) = 11.8%, and the Corrected Error Rate = IF / (C + INF + IF) = 1 / (14 + 2 + 1) = 5.9%. Thus, we have separate statistics for errors corrected and not corrected, and these statistics combine in an intuitive and meaningful way.
Note that these error rates correspond to the MSD error rate, and KSPC statistic, respectively. Although different in formulation, the Not Corrected Error Rate is what the MSD error rate was intended to be – a measure of the errors remaining in the transcribed text. Note though, that the Not Corrected Error Rate is a function of IF, and hence it cannot be found by analysing the transcribed text alone. In a similar vein, the corrected error rate provides a direct measure of the quantity that KSPC was intended to capture.
Since these three error rates are ratios of keystrokes; one final beneficial property is that they are independent of the characteristic KSPC of the text entry devices. Error rates measured using these formulations are comparable between different devices. This contrasts with the KSPC statistic, which, as noted above, is device dependent.
PUTTING THE STATISTICS THROUGH THEIR PACES
We have proposed a new framework for analysing errors in text entry tasks. It involves classifying keystrokes according to a taxonomy, and then calculating statistics from the size of each class. The approach is intuitive and seems reasonable, but will it work in an experimental setting? This question is addressed next.
An Experiment
One of the open questions in text entry research concerns the presentation of text to participants. At issue is the attention demand placed on participants [3]. Giving participants reams of text to enter forces them to attend to the presented text, the transcribed text, and possibly the input device (if it cannot be operated "eyes-free"). Yet when entering text into a mobile device in an office environment, users typically do not attend to any source text — usually they compose their own. So how is this scenario best simulated in an experiment? The presented text can be read aloud to the participants, but this approach is problematic [8].
Another option is to present participants with short phrases that are memorised. The participant studies each phrase and, when ready, enters it. The question is, should presented text remain on the screen while the participant enters it? Or, should it be removed from the screen as soon as entry begins? Leaving the phrase on the screen reduces the memory demands on the participant, and makes it easier for them to compare the transcribed text with the presented text, likely reducing the error rate. However, hiding the presented text better mimics the typical text entry task, as previously noted. In any case, the effect of removing the presented text is unknown.
Materials and Methods
Participants
Twelve unpaid volunteers participated in this study (four females, eight males). They ranged in age from 25 to 50, with an average age of 32.3 years. Ten were right-handed; two were left-handed (as reported by the participants).
Apparatus and Software
The input device was a Sharp EL-6053 pocket organiser (Figure 3). The EL-6053 is a typical personal information manager, employing a miniature Qwerty keyboard for text entry. The device is 124 mm × 84 mm × 10 mm (ignoring the protective cover). The alphabetic keys are 8 mm × 5 mm with a 3.6 mm gap between keys horizontally, and a 3.33 mm gap vertically. The space key is in the centre directly below the V key. The enter key is in the bottom right. The space and enter keys measure 19.5 mm × 5 mm.

Figure 3 - The modified Sharp EL-6053, showing the circuit board and protective cover underneath the keyboard
A PIC micro-controller (from Microchip Technology, http://www.microchip.com/) was interfaced to the keyboard hardware of the EL-6053, and programmed to emit ASCII characters in real time as keys were typed on the keyboard. The added circuitry increased the device thickness to 39 mm. ASCII characters were transmitted through a serial cable at 1200 baud to a host computer. A Java program time-stamped and recorded the ASCII characters. The Java program provided the look-and-feel of a simple text editor, so participants typing on the keyboard received visual feedback and confirmation of keystrokes. See Figure 4. (Note that the LCD screen in Figure 3 was not used.) Particular attention was paid to lag to ensure the accuracy of the final time-stamps.
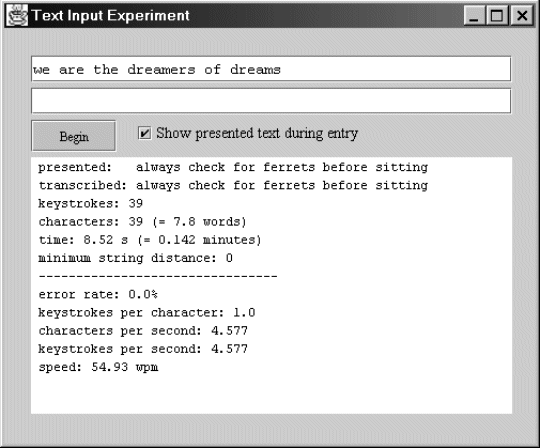
Figure 4 - A screen-print of the experimental software
A checkbox labeled "Show presented text during entry" is visible in Figure 4. This checkbox affects the behaviour of the presented text during the experiment. When checked, the presented text remains visible (in the top text bar) throughout each trial. When not checked, the presented text disappears with the first keystroke. As a participant types, the transcribed text appears in the second-from-top text bar in Figure 4. Each trial ended when the participant pressed the Enter key.
Procedure
Participants held the miniature Qwerty device in both hands. They were not allowed to place the device on the table in front of them, however they were allowed to rest their arms in any comfortable manner they wished. (This was done to mimic typical mobile device usage.) Participants were instructed to use both thumbs to enter text. They were allowed to rest or adjust themselves throughout the experiment (between trials). The specific instructions were to "enter the text as quickly and accurately as possible — as if typing e-mail to a colleague". The left cursor key functioned as backspace, the other cursor keys were disabled. The participants were instructed to use the backspace key for error correction.
Design
This is a within-subjects single-factor experiment with test conditions: presented text remains versus presented text disappears. The conditions were administered in a balanced manner, with participants randomly assigned to one of two groups. They performed 30 minutes of text entry for each condition.
Results
In total, the participants entered 857 phrases for the presented text remains condition, and, 819 for the disappears condition. The error statistics described earlier in this paper were calculated for each trial individually. Averages were then calculated for each participant. The results appear in Tables 2 and 3 below. Note that both the efficiency (Equation 6) and conscientiousness (Equation 7) become undefined if their denominators are zero. Efficiency is undefined if the participant performed no corrections, and the conscientiousness is undefined if no errors occurred. The values appearing in Tables 2 and 3 are averages including only trials where these statistics were defined.
The correlation between the conscientiousness values of both conditions was 0.81, indicating that the participants behaved relatively consistently under both conditions. However, an ANOVA reveals that the difference between the means of the two conditions (0.61 versus 0.78) was statistically significant (F1,11 = 23.1, p < .005). So there exists an interaction between the conditions and the conscientiousness.
The Error Rates
It appears upon inspection of Tables 2 and 3 that participants corrected more errors for the presented text remained condition. However, the corrected error rate was not significantly different between both conditions (F1,11 = 2.0, p > .1). Similarly, the total error rate did not significantly differ between the two conditions (F1,11 = 0.79, p > .3) either. However, a significant difference was measured for the not corrected error rate (F1,11 = 14.9, p < .005).
Results for Disappearing Presented Text condition
| Participant | MSD (chars) | KSPC (chars) | Old MSD Error Rate (%) | New MSD Error Rate (%) | Corrected Error Rate (%) | Not Corrected Error Rate (%) | Total Error Rate (%) | Wasted Bandwidth (%) | Efficiency | Conscient- iousness |
|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 1.36 | 1.08 | 3.38 | 3.31 | 3.37 | 3.30 | 6.67 | 9.43 | 1.000 | 0.56 |
| P2 | 0.31 | 1.58 | 0.78 | 0.78 | 16.06 | 0.68 | 16.74 | 24.00 | 1.000 | 0.86 |
| P3 | 0.89 | 1.07 | 2.17 | 2.16 | 2.78 | 2.10 | 4.88 | 6.92 | 1.000 | 0.54 |
| P4 | 2.11 | 1.57 | 5.13 | 5.10 | 18.84 | 4.07 | 22.90 | 33.20 | 1.000 | 0.80 |
| P5 | 2.51 | 1.09 | 6.20 | 6.10 | 2.88 | 6.03 | 8.91 | 10.95 | 1.000 | 0.25 |
| P6 | 0.54 | 1.17 | 1.41 | 1.40 | 6.11 | 1.31 | 7.42 | 11.01 | 1.000 | 0.62 |
| P7 | 0.99 | 1.18 | 2.30 | 2.30 | 7.15 | 2.13 | 9.28 | 14.40 | 1.000 | 0.74 |
| P8 | 0.98 | 1.04 | 2.66 | 2.64 | 2.01 | 2.62 | 4.63 | 6.30 | 1.000 | 0.45 |
| P9 | 0.24 | 1.16 | 0.56 | 0.55 | 5.26 | 0.55 | 5.81 | 8.77 | 1.000 | 0.76 |
| P10 | 0.45 | 1.27 | 1.07 | 1.06 | 9.04 | 0.99 | 10.02 | 14.93 | 1.000 | 0.70 |
| P11 | 1.15 | 1.03 | 2.58 | 2.57 | 1.31 | 2.53 | 3.84 | 5.00 | 1.000 | 0.34 |
| P12 | 0.87 | 1.19 | 2.19 | 2.17 | 7.61 | 2.04 | 9.65 | 15.03 | 1.000 | 0.77 |
| Mean: | 1.03 | 1.20 | 2.54 | 2.51 | 6.87 | 2.36 | 9.23 | 13.33 | 1.000 | 0.61 |
| SD: | 0.69 | 0.19 | 1.69 | 1.67 | 5.52 | 1.56 | 5.52 | 8.10 | 0.000 | 0.19 |
Results for the Remaining Presented Text condition
| Participant | MSD (chars) | KSPC (chars) | Old MSD Error Rate (%) | New MSD Error Rate (%) | Corrected Error Rate (%) | Not Corrected Error Rate (%) | Total Error Rate (%) | Wasted Bandwidth (%) | Efficiency | Conscient- iousness |
|---|---|---|---|---|---|---|---|---|---|---|
| P1 | 0.34 | 1.04 | 0.81 | 0.81 | 1.88 | 0.80 | 2.68 | 4.30 | 1.000 | 0.63 |
| P2 | 0.06 | 1.60 | 0.15 | 0.15 | 18.43 | 0.12 | 18.56 | 27.83 | 1.000 | 0.97 |
| P3 | 0.31 | 1.06 | 0.75 | 0.75 | 2.71 | 0.73 | 3.44 | 5.69 | 1.000 | 0.70 |
| P4 | 0.41 | 1.44 | 1.00 | 1.00 | 16.20 | 0.86 | 17.06 | 27.18 | 1.000 | 0.92 |
| P5 | 0.50 | 1.09 | 1.20 | 1.19 | 3.87 | 1.17 | 5.04 | 8.05 | 1.000 | 0.65 |
| P6 | 0.20 | 1.30 | 0.48 | 0.48 | 9.64 | 0.43 | 10.07 | 15.12 | 1.000 | 0.84 |
| P7 | 0.20 | 1.17 | 0.50 | 0.50 | 7.09 | 0.47 | 7.56 | 12.75 | 1.000 | 0.88 |
| P8 | 0.44 | 1.11 | 1.01 | 1.00 | 4.90 | 0.96 | 5.86 | 9.67 | 1.000 | 0.77 |
| P9 | 0.08 | 1.11 | 0.19 | 0.19 | 4.34 | 0.17 | 4.51 | 7.45 | 1.000 | 0.95 |
| P10 | 0.27 | 1.33 | 0.70 | 0.70 | 12.11 | 0.60 | 12.70 | 20.37 | 1.000 | 0.89 |
| P11 | 1.11 | 1.02 | 2.73 | 2.71 | 0.75 | 2.73 | 3.48 | 4.16 | 1.000 | 0.27 |
| P12 | 0.20 | 1.30 | 0.50 | 0.50 | 10.70 | 0.46 | 11.16 | 17.80 | 0.998 | 0.89 |
| Mean: | 0.34 | 1.21 | 0.84 | 0.83 | 7.72 | 0.79 | 8.51 | 13.37 | 1.000 | 0.78 |
| SD: | 0.28 | 0.18 | 0.68 | 0.67 | 5.73 | 0.68 | 5.41 | 8.39 | 0.000 | 0.20 |
Words per Minute
Participants were faster (27.1 wpm) with the disappears condition than with the remains condition (25.3 wpm) (F1,11 = 12.7, p < .005).
Discussion
General Observations
It is not surprising that nearly every participant performed with a 1.000 efficiency. The only means available to the participants to correct errors was the backspace key. So, every keystroke of correction could affect only one keystroke of errors. But how did participant 12 ("P12") achieve a less than 1.000 efficiency for the remaining presented text condition? During two trials the participant committed an error at the very beginning of the trial, and used one too many backspace key presses to correct the error. Backspace has no effect if the cursor is already at the beginning, although it still counts as a fix keystroke.
The commonality of the efficiency values contrasts with the variability of the conscientiousness values. P2 had a much lower not corrected error rate than P11, for both conditions. However, P2 also had the highest total error rate, while P11 had the lowest. These values seem to contradict, until one notices that P2 was very conscientious, while P11 was not.
Participants were generally more conscientious when the presented text remained visible, making it easier to observe their mistakes. (Note also that because the presented text was visibly aligned above the transcribed text, it was easy for participants to identify errors, see Figure 4.) However, participants each had a unique level of conscientiousness that was observable under both conditions. We reason that participants did correct more errors when the presented text remained, but because most errors were corrected, the effect on the corrected error rate was not pronounced enough to be statistically significant. Clearly, though, fewer errors went uncorrected under the presented text remains condition.
Effects of the speed-accuracy trade-off are apparent in these results. Text entry proceeded slightly faster when the presented text was hidden during the trial. Presumably, leaving the presented text visible to participants tempts them to spend additional time searching for errors. This sways their behaviour toward the accuracy end of the speed-accuracy continuum. Conversely the disappearing presented text condition removes the distraction of easy error searching, and thus influences participants towards speed.
The parallel between the MSD error rate and KSPC statistic pair, and the corrected and not corrected error rates, is apparent. The new statistics proposed in this paper seem to perform similarly to their older counterparts. In particular, the numerical values of the not corrected error rate, and both new and old MSD error rates, are all very similar across participants.
The values in the corrected error rate columns of Tables 2 and 3 represent errors that would have gone unaccounted for, prior to the introduction of the new error measures.
Notice that there is no apparent relationship between the total error rate and conscientiousness. Correlations between total error rate and conscientiousness, for both conditions, do not exceed 0.31. This suggests that there is some factor that affects each participant's error rate, that is independent of their desire for correctness.
Participants performed similarly with respect to wasted bandwidth in both conditions. The correlation of the wasted bandwidth figures for both conditions was 0.89.
CONCLUSIONS AND FUTURE WORK
In this paper we have presented criticisms of the MSD error rate and KSPC statistic. A framework has been developed that provides a new perspective on error analysis. Several new statistics have been proposed, including total error rate, corrected error rate, and not corrected error rate. The latter two are proposed as replacements for the MSD error rate and KSPC. These new error rates have the following useful properties:
- The total error rate reflects all errors committed by a participant (corrected and not).
- Total error rate cleanly separates into two constituents, corrected error rate, and not corrected error rate.
- The error rates are device independent. They are directly comparable and do not misstate the performance of text entry methods with inherently different KSPC characteristics.
We have also presented the results of a study to determine the effect the persistence or absence of presented text has on text entry. By hiding the presented text from participants once the first keystroke of a trial begins, experimenters can expect a higher text entry speed, accompanied by a higher not corrected error rate. While we are satisfied that we were able to detect the speed-accuracy trade-off, further work is needed to determine the relationship between these error rate metrics (i.e. accuracy), and speed. A means to measure the bandwidth of the interaction between humans and machines during text entry, that encompasses both speed and accuracy, remains to be found. Such a measure would be the ideal way to compare text entry methods.
We would like to see this framework extended to account for non-keyboard-based text entry methods. In typical desktop text entry, the mouse may be used to move the cursor, or select text. A means to include this rich form of text interaction into these analyses is highly desirable.
ACKNOWLEDGMENTS
This work was supported by the NSERC, Canada, and the Academy of Finland (project 53796).
REFERENCES
1. MacKenzie, I.S., Kober, H., Smith, D., Jones, T., and Skepner, E. (2001) LetterWise: Prefix-based disambiguation for mobile text entry, Proceedings of the ACM Symposium on User Interface Software and Technology - UIST 2001, pp. 111-120. New York: ACM.
2. MacKenzie, I. S. (2002) KSPC (keystrokes per character) as a characteristic of text entry techniques, Proceedings of the Fourth International Symposium on Human-Computer Interaction with Mobile Devices. Heidelberg, Germany: Springer-Verlag.
3. MacKenzie, I. S. and Soukoreff, R. W. (2002) Text entry for mobile computing: Models and methods, theory and practice. Human-Computer Interaction, 17 (2 & 3), pp. 147-198.
4. MacKenzie, I. S. and Soukoreff, R. W. (2002) A character-level error analysis technique for evaluating text entry methods, Proceedings of the Second Nordic Conference on Human-Computer Interaction - NordiCHI 2002, pp. 241-244. New York: ACM.
5. Matias, E., MacKenzie, I. S., and Buxton, W. (1993) Half-Qwerty: A one-handed keyboard facilitating skill transfer from Qwerty, Proceedings of the ACM Conference on Human Factors in Computing Systems - INTERCHI '93, 88-94. New York, ACM.
6. Shannon, C. E., (1951) Prediction and entropy of printed English. Bell System Technical Journal, 30, 51-64.
7. Soukoreff, R. W. and MacKenzie, I. S. (2001) Measuring errors in text entry tasks: An application of the Levenshtein string distance statistic, Companion Proceedings of the ACM Conference on Human Factors in Computing Systems - CHI 2001, pp. 319-320. New York: ACM.
8. Ward, D. J., Blackwell, A. F., and MacKay, D. J. C. (2000) Dasher: A data entry interface using continuous gestures and language models, Proceedings of the ACM Symposium on User Interface Software and Technology - UIST 2000, pp. 129-137. New York: ACM.
-----
- As well as the KSPC statistic, corrected errors also affect the speed of text entry. We will return to this point later.
- Multi-tap is a common text input method for mobile phones. With this approach, the user presses each key one or more times to specify the input character. For example, the 2 key is pressed once for the character A, twice for B, three times for C.
- Note that the INF class also includes characters mistakenly omitted from the transcribed text. So INF contains any errors that are not rectified by the subject - extra characters (insertions), incorrect characters (substitutions), and omitted characters (deletions).
- As only the size of the sets is required, we introduce a simplification: INF = MSD(P, T), and C = max(|P|, |T|) - MSD(P, T). The sizes of the IF and F sets are found by scanning the input stream.
- Purists will rightfully disagree. The units of C, INF, IF, and F, are characters, not bits. Yet Shannon [6] argues that it is possible to measure the information content of a character. A future direction for this work is to cast these formulae in terms of information content, instead of characters. Then these relations would also apply to non-character-based text input methods. Equations 8 and 9 represent a first step toward this goal.