MacKenzie, I. S., & Teather, R. J. (2012). FittsTilt: The application of Fitts' law to tilt-based interaction. Proceedings of the Seventh Nordic Conference on Human-Computer Interaction – NordiCHI 2012, pp. 568-577. New York: ACM. doi:10.1145/2399016.2399103 [PDF] [video] [software]
FittsTilt: The Application of Fitts' Law To Tilt-based Interaction
I. Scott MacKenzie, & Robert J. Teather
Dept. of Computer Science and EngineeringYork University
4700 Keele Street
Toronto, Ontario, M3J 1P3 Canada
+1 416 736-2100
{mack,rteather}@cse.yorku.ca
ABSTRACT
We evaluated tilt as an input method for devices with built-in accelerometers, such as touchscreen phones and tablet computers. The evaluation was empirical and experimental. Sixteen participants performed a tilt-based position-select task, similar to the multi-directional Fitts' law task in ISO 9241-9. Four levels of tilt gain (25, 50, 100, and 200) and two selection modes (first-entry and 500 ms dwell) were used. Movement times were lowest with tilt gain = 50 and first-entry selection. Maximum tilt angles ranged from about 2° to 13°, depending on condition. Tilt as an input primitive is shown to conform to Fitts' law. Throughput is low, however, about 2.3 bits/s for first-entry and 1.2 bits/s for dwell.ACM Classification: H.5.2 [Information interfaces and presentation]: User Interfaces – Input devices and strategies
General Terms: Performance, Human Factors.
Keywords: tilt, accelerometer, mobile devices, touchscreens, tablet computers, Fitts' law, ISO 9241-9, human performance
INTRODUCTION
Since 2007, with the release of the Apple iPhone, touchscreen phones and tablet computers have shifted the landscape of human-computer interaction for mobile computing. Pressing keys on small keyboards has given way to finger actions: swiping, flicking, pinching, tapping, and so on. Most devices in this genre include additional components to enhance the user experience. Cameras, light sensors, vibro-tactile actuators, accelerometers, gyroscopes, GPS receivers, and so on, work together in broadening the experience for users. With the prefix "smart", these devices are full-fledged media players, providing unprecedented connectivity to users, through both 3G and Internet access.
In this paper, we examine tilt as an interaction primitive for mobile devices, such as touchscreen phones and tablet computers. Our interest is human performance: How well can users control an on-screen object using the tilt of the device as input? What parameters of tilt influence human performance and what are the performance outcomes under different settings of these parameters? Does tilt input conform to Fitts' law, as with input from devices such as mice and joysticks? What is throughput (bits/s) for tilt-based interaction?
This paper is the first general investigation of tilt as an input primitive. The goal is to lay the foundation for empirical inquiry of tilt and other novel interaction primitives where human performance issues are present. We begin with an overview of prior research into tilt as an input primitive. Then we examine human performance and how this might be evaluated for interactions using tilt as an input primitive. This is followed with a user study where parameters of interaction, including tilt gain, are manipulated while human performance is measured and analysed in a simple tilt-based task.
Tilt as an Input Primitive
Devices with built-in accelerometers can use the motion or tilt of the device as an input primitive. Early research on tilt, dating to the 1990s, examined its potential for tasks such as document scrolling [1, 5, 15], panning and zooming [15], menu navigation [13], and changing screen orientation [8]. As with any new technology, research initially focused on what can be done rather than on how well it can be done. The focus was on the technology and its integration in prototype devices. Test results with users tended to be anecdotal, not empirical. Some examples from the literature include "[users] were able to quickly adjust with practice" [5, p. 22], "users found it easy to operate" [1, p. 44], or "users could control the tilt quite precisely" [13, p. 168].
Tilt-based interaction has been used for mobile text entry [12, 14, 19]. This is one specialized area where empirical studies have been reported, especially to compare tilt- and button-based text entry. For example, Wigdor and Balakrishnan [19] used device tilt to disambiguate letter selection for mobile text entry and compared this to MultiTap. With tilt, they found higher text entry speeds, but also higher error rates. The Unigesture method [14] partitioned letters into seven "zones" corresponding to seven tilt directions, with the eighth direction reserved for the SPACE key. It uses disambiguation (similar to T9) to infer what the user is entering. TiltType [12] is similar, but accesses letter groups via buttons and uses tilt to disambiguate. While these studies demonstrate the effectiveness of tilt-based interaction for text entry, they do not indicate what kind of performance tilt affords in general interaction tasks, such as selecting user interface widgets.
Camera-based device tilt has been used for 3D object manipulation using a mobile phone in augmented reality. The results are somewhat mixed. For example, work by Henrysson et al. [6] used phone tilt to control the orientation of 3D objects. The authors compared four techniques for one-axis rotation. The techniques included two using tilt/orientation, one using phone displacement, and one using keys. Both tilt methods were significantly slower than the other methods. A later study [7] compared tilt to key/joystick and touchscreen input. Ultimately, the key-based method offered fastest object rotation times, and was more preferred by participants. This may be due to the clutching necessitated by the tilt technique. However, tilt did outperform the touchscreen method, suggesting some positive benefits in using tilt for input control.
Gaming is another area where tilt is frequently employed. Device tilt can be used to control the speed or direction of a moving object. This has been commonly employed in commercial games on mobile devices since tilt interaction became available. It is also commonly used in game consoles with tilt-sensitive controllers, e.g., the Nintendo Wii. Where human interaction is studied, the evaluations are often qualitative and non-experimental. Gilbertson et al. [4], for example, compared mobile phone tilt with button input in a driving game, with tilt or buttons controlling the acceleration or breaking of a car. The evaluation was informal, focusing on the user experience. Users offered comments such as "that's so cool" or "this is more fun".
Another example is the work of Valente et al. [17] who investigated mobile accessible games for the visually impaired. Phone tilt controlled player movement while navigating a maze. Sound and haptic feedback (vibration) indicated when the player hit a wall, or was moving through the environment. Their study was qualitative, focusing on observations and interviews. Participants generally found tilt-based interaction natural and usable, although some recommended alternative control schemes (e.g., joysticks).
Although game research on tilt control is predominantly qualitative in nature, some studies also employ quantitative methods. For example, Browne and Anand [2] compared three interfaces for a shooting game on an Apple iPod Touch. The interactions included tilt, gestures, and on-screen buttons. Although the evaluation was primarily qualitative, they also included empirical measures, reporting that participants were able to play significantly longer using tilt. They suggest that tilt should be included in commercial games on these platforms.
One of the few empirical studies of general tilt-based interaction uses a camera-based approach for detecting motion [18]. Although tilt is usually implemented using an accelerometer, Wang et al. [18] used vision-based motion tracking software and proposed several interaction tasks to use it. These include a point-select task, game control, and text entry. The pointing task is probably the closest to our evaluation. Like our study, the authors also employed Fitts' law [3], but only investigated 1D cursor control in four directions. This may be due to imprecision in the sensing method. Ultimately, performance of this interaction technique was poor (≈1 bps). The authors note that accelerometers have advantages over cameras. In particular, accelerometers reduce the processing requirements and consequently also reduce power consumption.
Our study investigates general pointing tasks in the context of Fitts' law [3]. Unlike previous work, we employ the ISO 9241-9 standard [9] multi-directional pointing task. As well, our experiment manipulated a fundamental property of tilt: tilt gain. Before presenting our methodology, we discuss Fitts' law and the ISO 9241 9 evaluation methodology.
USER PERFORMANCE EVALUATION
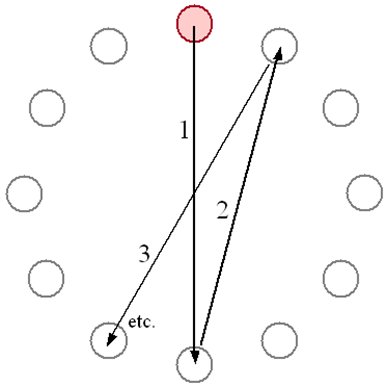
The ISO 9241-9 [9] standard is directed at the evaluation of non-keyboard input devices. Tilt as an input primitive seems to apply, since tilting actions can be used for input control and key actions are not involved. The standard proposes a methodology for evaluating performance and comfort. The most widely used of the performance tasks is the multi-directional point-select task, where the user selects targets arranged in a layout circle. For each trial, the position of the target changes, according to a predictable pattern. See Figure 1. For tilt, the task is positioning, not pointing, but the goal is similar. In fact, the task seems well suited to tilt, since angles from 0° to 360° are required.
Figure 1. ISO 9241-9 multi-directional position-select task.
In most cases, the task in Figure 1 involves positioning a cursor. For tilt, a virtual object such as a ball could be used instead of a cursor. Target selection is a challenge, however. One possibility for tilt is "first entry" where a trial finishes when the ball first enters the destination circle. Another possibility is "dwell", where a trial finishes after the ball is held inside the destination circle for a prescribed time interval. Obviously, dwell would be harder. How much harder is an issue for empirical inquiry, as examined below.
Positioning a ball inside a destination circle is similar to the pin transfer task used in the original experiment leading to Fitts' law [3]. The task required participants to move a round pin across a movement amplitude, A, and position the pin inside a target circle of width, W. Fitts proposed to quantify such tasks with an index of difficulty (in bits), which today takes the form
. (1)
Fitts noted that for the pin transfer task, target width "is the difference in inches between the diameter of the pins and the diameter of the hole into which they were inserted" [3, p. 266]. The main dependent variables for the task in Figure 1 are speed, accuracy, and throughput. Throughput (TP, in bits/second) is computed by dividing the index of difficulty (ID, in bits) by the average movement time (MT, in seconds):
. (2)
Although throughput normally includes an adjustment for accuracy, this is problematic for the proposed tilt task since there is no possibility for an error: A trial continues until the ball is correctly positioned inside the target circle. Accuracy can be measured in others ways, however, such as target re-entries (for dwell-based selection) or the movement variability. Movement variability is the extent to which the sample points for the ball's path lay along a straight line parallel to a line between the source and destination targets [10]. Speed is typically measured as the mean movement time (ms) for trials. For tilt input, another possible dependent variable is the maximum tilt angle.
METHOD
In view of the recent and now common use of tilt as an input primitive, we sought to evaluate tilt input according to conventional practices for empirical research in HCI. In this section we describe the methodology for a user study that includes independent and dependent variables, a representative task, measurement of human performance, data collection and analysis, and so on. As well, the methodology was designed to test the question noted earlier on whether tilt input conforms to Fitts' law.
Participants
Sixteen participants were recruited from the local university campus. There were 9 males and 7 females, ranging in age from 19 to 39 years (mean = 26, SD = 5.0). Most participants reported little familiarity with tilt-based interaction: Six had never used it and eight reported using it only infrequently (a few times per month). The remaining two participants used tilt-based interaction more frequently.
Apparatus
The experiment was performed using a Samsung Galaxy Tab 10.1 running Google's Android 3.1 (Honeycomb) operating system. See Figure 2.
Figure 2. Samsung Galaxy Tab 10.1.
Software was developed in Java using the Android SDK, with special focus on the SensorManager class. Tilt control was implemented using the device's built-in accelerometer, manufactured by InvenSense (http://invensense.com). The sensor was configured to operate at the "game" sampling rate (about 50 Hz). Sensor events occurred approximately every 20 ms, providing tablet pitch and roll data to the experiment software. Raw pitch and roll values were converted to tilt magnitude and tilt angle1 as follows (details are simplified):
(3)
. (4)
These data were used to control the direction and velocity of a virtual rolling ball in the interface. The velocity (v, in pixels/second) of the ball was a linear function of tilt magnitude and a programmable tilt gain setting:
. (5)
With each sample, the ball displacement (dBall, in pixels) was calculated as the product of the velocity and time since the last sample (dt, in seconds):
. (6)
As an example, if the tilt magnitude was sampled at 3° and tilt gain was set at 50, then velocity was 3 × 50 = 150 pixels per second. If the sample occurred 20 ms after the previous sample, the ball was moved 0.02 × 150 = 3.0 pixels in the direction of the tilt angle. After extensive pilot testing, four tilt gain settings were chosen for the user study: 25, 50, 100, and 200.
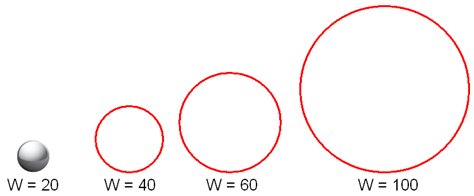
The task implemented in software was to tilt the device to control the direction and speed of a virtual ball and to move the ball from one target circle to the next, according to the pattern described above (see Figure 1). The virtual ball was 20 pixels in diameter. Three sizes of target circles were used: W = 40, 60, and 100 pixels. See Figure 3.
Figure 3. Experiment conditions. A ball (left) was moved and positioned inside three sizes of targets.
There were twelve target circles arranged in a layout circle. Three layout diameters were used: A = 125, 250, and 500 pixels. The layout and target diameters were chosen to ensure the tasks covered a reasonable range of difficulties, according to Fitts' law. With the adjustment noted above to subtract the ball diameter from the target circle diameter, the task difficulties ranged from
(7)
to
. (8)
Figure 4 shows two examples of experiment conditions.
(a) (b)
Figure 4. Example conditions (a) A = 125 pixels, W = 60 pixels. (b) A = 500 pixels, W = 100 pixels. (Note: 500 pixels = 8.5 cm)
Besides manipulating A, W, and tilt gain, the experiment software included a parameter for the selection mode. The two selection modes discussed above were implemented: first entry and dwell. For the dwell condition, 500 ms was used, as seemed reasonable based on pilot tests. Both selection modes required the ball to be completely within the target circle.
The experiment also included a questionnaire, with items similar to those in ISO 9241-9. In addition to collecting demographic information, the questionnaire was intended to assess participant preference for the experimental parameters. It also elicited subjective measures of comfort, mental effort, and perceived performance. Questions also included subjective assessment of operation smoothness, and overall ease of use.
Procedure
After signing a consent form and being briefed on the goals of the experiment, the experiment task was demonstrated to participants. Participants were seated during the experiment and held the tablet in whatever position they felt was comfortable. See Figure 5.
Figure 5. A participant performing the tilt-based position-select task.
Prior to each condition, participants were given the tablet and were allowed to perform one or more sequences of practice trials before data collection began. A sequence consisted of twelve target selections, as per Figure 4. A block consisted of nine sequences (3 amplitudes × 3 widths) presented in random order. Participants were divided into four groups. The tilt gain conditions were presented according to a 4 × 4 balanced Latin square. The selection mode conditions were counterbalanced within the tilt gain conditions.
Design
The experiment had the following independent variables and levels:
- Tilt gain: 25, 50, 100, 200
- Selection mode: First_entry, Dwell_500
- Target amplitude: 125, 250, 500 pixels
- Target width: 40, 60, 100 pixels
The dependent variables were movement time, target re-entries (for the dwell condition), movement variability, maximum tilt angle, and throughput. As well, a questionnaire was administered at the end of testing to solicit participant opinions on tilt-based interaction and the experiment task.
Testing lasted about one hour per participant. The total number of trials was 16 participants × 4 tilt gains × 2 selection modes × 3 target amplitudes × 3 target widths × 12 selections per sequence = 13,824.
RESULTS AND DISCUSSION
Movement Time
The mean movement time per trial over the entire experiment was 2026 ms. As expected, the effect of selection mode on movement time was statistically significant (F1,12 = 591.2, p < .001). At 2647 ms, the mean for the Dwell_500 condition was 88.5% longer than the mean of 1404 ms for the First_entry condition. This is well beyond the inherent difference of 500 ms, and can be attributed to challenges in controlling the ball with higher tilt gain settings and the need to proceed cautiously as the ball approached the target circle in the dwell condition.
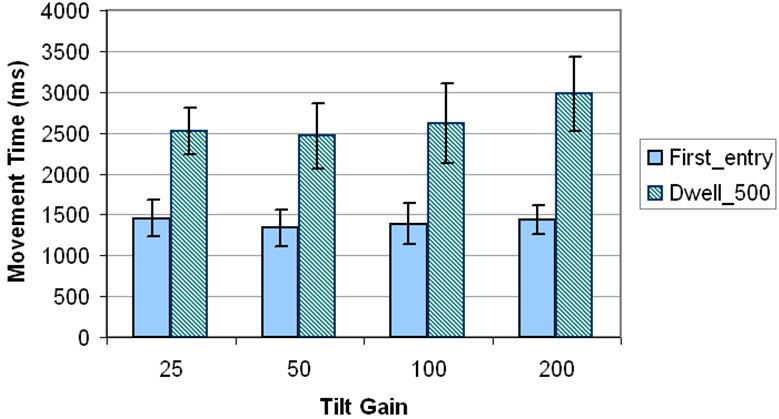
The effect of tilt gain on movement time was also statistically significant (F3,36 = 11.9, p < .001). Tilt gain = 50 produced the lowest movement time (1900 ms), with tilt gain = 200 the highest (2210 ms). See Figure 6. A Tukey-Kramer post hoc test (p < .05) showed that only the 50-200 tilt gain comparisons were significantly different.
Figure 6. Movement time (ms) by selection mode and tilt gain. Error bars show ±1 SD.
Accuracy
Although the experiment software collected seven accuracy measures (described in [10]), the most revealing are movement variability and target re-entries.
The results for movement variability are shown in Figure 7. The mean variability was between 7 and 19 pixels of a direct path for all conditions. The effects were statistically significant both for selection mode (F1,12 = 24.7, p < .001) and tilt gain (F3,36 = 59.1, p < .001). Note that while movement time was less with First_entry selection, movement variability was less with Dwell_500 selection. This was likely due to participants tilting the tablet and moving the ball more cautiously in the Dwell_500 condition, due to the greater difficulty in final selection.
This effect was observed during the experiment. Participant behaviour with the First_entry condition was somewhat reckless; after becoming familiar with the target pattern, participants would very quickly tilt the tablet yielding higher movement speed, and greater tilt angles (maximum tilt is discussed further below). Effectively, they would roll the ball through the target and then continue on the path to the next target, rather than attempting to stop in the target. The added precision requirement of the Dwell_500 condition eliminated this behavior, resulting in more cautious movement.
Figure 7. Movement variability (pixels) by selection mode and tilt gain. Error bars show ±1 SD.
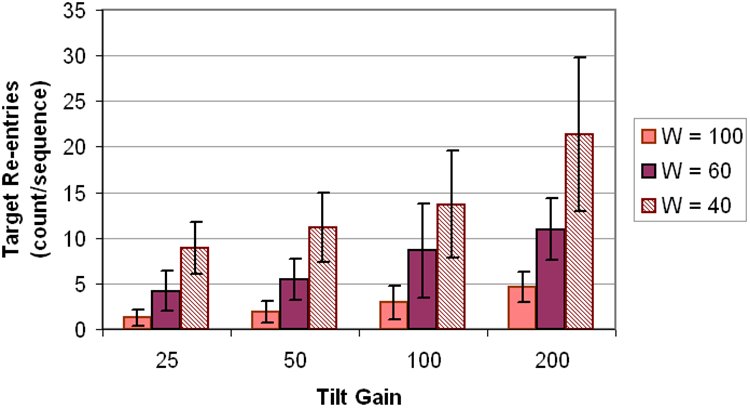
Target re-entries is a count of the number of times the ball re-entered the target circle after having entered it once. It is reported here on a per-sequence basis. Obviously, this measure only applies to the Dwell_500 condition. The trends were as expected: Participants have more difficulty with final selection for smaller targets and with higher tilt gains. See Figure 8.
Figure 8. Target re-entries (count/sequence) by tilt gain and target width for the Dwell_500 selection mode. Error bars show ±1 SD.
The most difficult condition was tilt gain = 200 and target width = 40 pixels, with an average of 21.4 target re-entries per sequence. Under this condition, the tablet was very sensitive to changes in tilt and any such change tended to move the ball out of the small target circle, necessitating re-positioning. Participants also frequently commented on the difficulty of successfully holding the ball steady in small targets in the Dwell_500 condition.
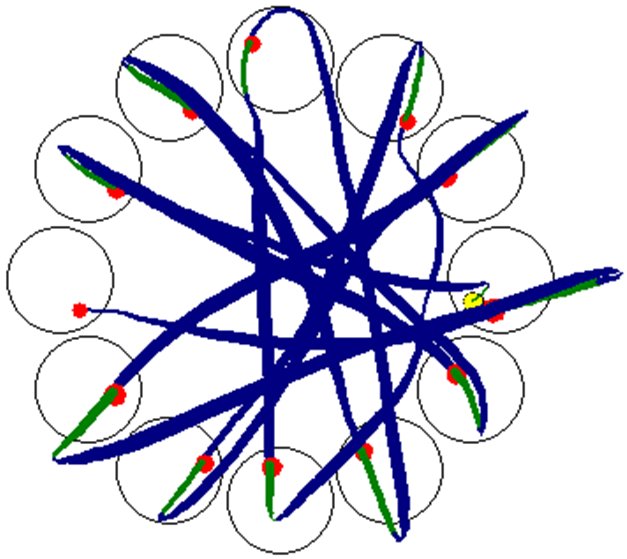
As an example, Figure 9 is a trace plot for participant #16 for tilt gain = 200, Dwell_500, A = 500, and W = 40. In all, there are 32 target re-entries. The yellow dot (target at 3 o'clock) shows the beginning of the sequence. Each red dot shows the final coordinate of the center of the ball upon selection. Many of the target re-entries occurred with the ball "partially inside" the target. Clearly, with the highest tilt gain setting of 200, the participant had considerable difficulty stabilizing the tablet for final selection. The mean movement time per trial was a substantial 5260 ms. This consisted of 2296 ms for positioning (start of trial to first entry) and 2964 ms for selecting (first entry to final selection). Thus, the participant took longer to select the destination target than to maneuver the ball over the required distance.
Figure 9. Trace example. See text for discussion.
Maximum Tilt
The experiment software logged the maximum tilt angle for each trial. To avoid reporting anomalous tilt actions, maximum tilt is reported here as the mean of the individual maximums over a sequence of 12 trials. The results are shown in Figure 10. Clearly, there is a relationship between tilt gain and the amount of tilt participants use to accomplish tasks. At tilt gain = 25, the maximum tilt angle was 12.8°. This decreased dramatically to 2.6° at tilt gain = 200.
Figure 10. Maximum tilt by tilt gain and selection mode. Error bars show ±1 SD.
The effect of tilt gain on maximum tilt was statistically significant (F3,36 = 267.3, p < .001). The effect of selection mode was also statistically significant (F1,12 = 36.7, p < .001), although less dramatic. For each tilt gain setting, the maximum tilt angle was about 22% less for Dwell_500 selection compared to First_entry. Again, this effect is attributed to the participants proceeding more cautiously with dwell selection.
Our trace plots show tilt angle as thickness in the traces. In the example above (Figure 9) the maximum tilt was 4.1°, which is slightly higher than the mean (right-side bar in Figure 10). As evident in Figure 10, participants tilted the tablet substantially more for lower tilt gains – to move the ball more quickly to the destination target. An example for participant #10 is shown in Figure 11. This is for tilt gain = 25 combined with First_entry selection (left-side bar in Figure 10). The target conditions are A = 250, W = 60. Very aggressive tilting is evident, as was observed during the experiment. The maximum tilt was 16.2°. (The beginning of each trial is shown in green.) The participant tilted the tablet substantially and quickly, anticipating immediate selection when the ball entered the target. Some overshoot is evident in the traces. The mean movement time per trial for this sequence was 1219 ms.
Figure 11. Trace example. See text for discussion.
Fitts' Law and Tilt-based Input
As noted earlier, the target amplitude (A) and target width (W) values were chosen to ensure the tasks covered a reasonable range of difficulty. This is also important in examining whether the task in question – tilting – conforms to Fitts' law. A Fitts' law model is built by regressing the mean movement times (MT) on the associated A-W conditions, with each A-W condition expressed as an index of difficulty (ID) according to Equation 1. The result is a regression equation of the form
. (9)
where a and b are the intercept and slope coefficients for the best-fitting line. The fit of the model is usually associated the correlation (r) or the squared correlation (R2). The higher the correlation, the better the fit. Correlations for computer pointing devices in Fitts' law tasks are routinely .9 or higher (e.g., [11, 21]).
Fitts' law models were built separately for each tilt gain setting and for each selection mode. Table 1 summarizes the models. The fit of the model was good in all cases, with squared correlations from R2 = .8841 to R2 = .9923. A desirable quality of a Fitts' law model is a near-zero intercept. Six of the models in Table 1 have intercepts less than 100 ms. However, two models have rather large intercepts (>|200 ms|). These occurred for the harder selection mode (Dwell_500) and for the largest and smallest tilt gain settings. There are, perhaps, compensatory behaviours present here that compromise the Fitts' law models. However, the highest R2 value occurred for the condition with a = 222.9 ms; so, an additional explanation may be needed.
Fitts' Law Models for Tilt-based Interaction
| Tilt Gain | First_entry | Dwell_500 | ||||
|---|---|---|---|---|---|---|
| Intercept (a) | Slope (b) | R2 | Intercept (a) | Slope (b) | R2 | |
| 25 | 38.6 | 486 | .9654 | 222.9 | 789 | .9923 |
| 50 | 91.6 | 427 | .9829 | 91.7 | 814 | .9810 |
| 100 | 11.1 | 473 | .9648 | 13.5 | 894 | .9668 |
| 200 | 7.6 | 491 | .9443 | -270.6 | 1116 | .8841 |
| Note: Regression equations are of the form MT = a + b × ID. | ||||||
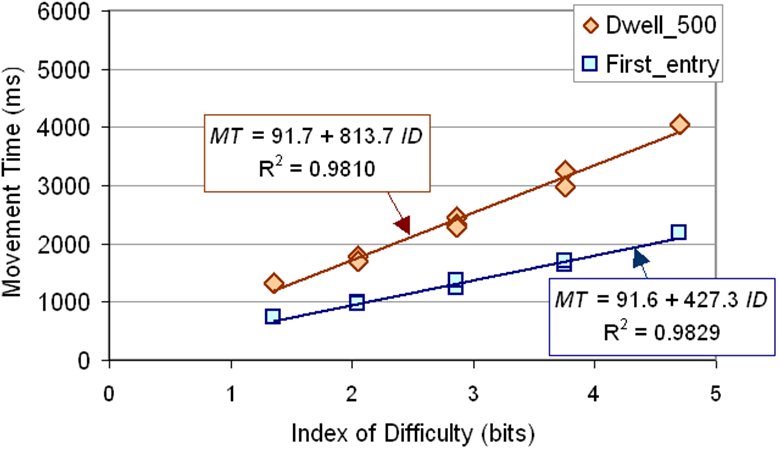
Figure 12. Fitts' law models for tilt gain = 50.
For both models in Figure 12, the sample points are clustered close to the regression lines. Of course, this is fully expected due to the high correlations. For the First_entry condition, for example, the model accounts for 98.3% of the variation in the observations. Clearly, tilt-based position-select tasks conform to Fitts' law. For performance comparisons among the test conditions and with other input methods, we turn to Fitts' throughput.
Fitts' Throughput
Besides model fitting and building prediction equations, Fitts' law allows human performance to be quantified in information terms. Fitts' index of performance, now throughput, is the human rate of information processing (in bits/s) in performing the task under investigation. Although throughput today usually includes an adjustment for accuracy, this is not practical for the tilt-based task in our experiment, because there was no possibility of an error. However, it is still possible (and common) to compute throughput considering only movement time (MT) and the index of difficulty (ID) for the experiment tasks.
In the literature on Fitts' law, throughput is computed either using the slope reciprocal from the regression line (1 / b) or by a division of means (ID / MT). Although there is controversy on which method is better (see [16, 20] for discussions), we avoid this here by presenting both values. See Table 2. Throughputs for tilt-based interaction ranged from 0.90 bits/s to 2.46 bits/s. The differences between the two methods of calculation range from −5.2% to +14.5%, suggesting that, indeed, there are underlying and outstanding issues on how to calculate throughput.
Throughput (bits/s) By Condition
| Condition | Throughput (bits/s) | |||
|---|---|---|---|---|
| Selection mode | Tilt gain | 1 / b | ID / MT | Difference (%) |
| First_entry | 25 | 2.06 | 2.22 | 7.3% |
| First_entry | 50 | 2.34 | 2.45 | 4.6% |
| First_entry | 100 | 2.12 | 2.46 | 14.0% |
| First_entry | 200 | 2.04 | 2.39 | 14.5% |
| Dwell_500 | 25 | 1.27 | 1.20 | -5.2% |
| Dwell_50 | 50 | 1.23 | 1.26 | 2.7% |
| Dwell_500 | 100 | 1.12 | 1.22 | 8.3% |
| Dwell_500 | 200 | 0.90 | 1.12 | 19.9% |
| Note: Values are given using the slope reciprocal (1 / b) and the division of means (ID / MT). | ||||
Note that for First_entry selection, the tilt gain settings bracket the preferred outcome. Throughputs were lower for tilt gains of 25 and 200 than for tilt gains of 50 and 100. Similarly, on movement time, the tilt gains of 25 and 200 yielded poorer results (i.e., higher MT; see Figure 6). Overall, tilt gain in the range of 50-100 is likely optimal for tilt-based interaction, although further testing at a finer granularity is needed.
Two additional observations are relevant in Table 2. First, throughput for Dwell_500 selection at 0.90-1.27 bits/s is only about half that for First_entry selection at 2.04-2.46 bits/s. Clearly, first-entry selection is preferred over dwell-based selection, where interactions allow. Second, the values in Table 2 are well below the throughput values for the mouse, which are commonly in the range of 4-5 bits/s for multi-direction point-select tasks such as employed here [20, Table 4]. However, the values in Table 2 are similar to values for other pointing devices such as the touchpad and isometric joystick, where throughputs in the range of 1.4-2.9 bits/s are reported [20, Table 4].
Participant Feedback
Following the experiment, participants completed a short survey, with response items similar to those in ISO 9241-9 [9]. The survey was not intended to compare the selection modes or tilt gain settings, but rather to establish overall how participants felt about using tilt control for this type of target selection task.
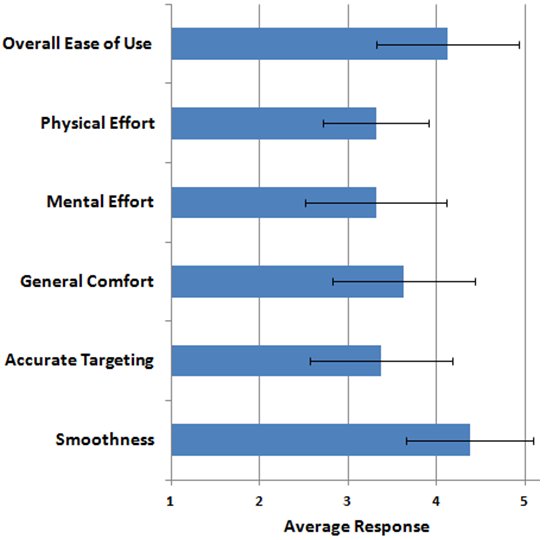
Likert-scale questions were designed to assess both physical and mental effort, as well as comfort and ease of use. The questions addressed targeting accuracy and smoothness during operation. There were also questions relating to the experimental factors (i.e., selection mode and tilt gain). The results are summarized in Figure 13. (For all items, five is the most favourable response.)
Figure 13. Participant responses to survey questions. In all cases, a higher score is better (e.g., for Physical and Mental Effort, a higher score indicates lower effort). Error bars show ±1 SD.
Overall, the results are favourable for tilt-based input. The means were above the neutral category (3) for all items and between "somewhat" (4) and "very" (5) for overall ease of use and smoothness.
The survey also asked participants which selection mode they preferred. All but one participant preferred First_entry selection. One participant indicated that he had no preference between the two selection methods. He felt that first entry was "too sensitive" while dwell took too long.
Finally, the survey also asked which tilt gain setting was preferred. Eleven participants preferred a tilt gain of 100. Three preferred the fastest tilt gain setting, 200, while two preferred a tilt gain of 50. No participant preferred the slowest tilt gain setting of 25, and many commented while using this condition that it simply felt too slow. One participant that preferred tilt gain of 100, indicated that except for large targets the fastest setting was too sensitive to control accurately. This participant also indicated that the slower tilt gain settings were "annoying". A participant that preferred a tilt gain of 50 indicated that the slower speed improved aiming precision. Another participant suggested that the higher speeds would be impractical for use in a truly mobile context, for example, while riding a subway train.
Finally, several participants suggested that the dwell period was too long, and hindered their performance in this condition. This is reflected in our results. Unsurprisingly, several participants also indicated that dwell was especially difficult to use for small targets.
Future Work
Several potential avenues for future work are available. While our study investigated the performance of rate control of the cursor, position control is also possible. In a sense, mapping tilt magnitude to object position is like tilting a joystick to control a cursor. Another possibility is to investigate a different task. The multi-dimensional reciprocal tapping task is a useful performance task, but is somewhat abstract. Given that tilt control is often used in games (e.g., the popular "marble maze" styled games), a natural follow-up would be to look at more game-like path-following tasks.
Finally, a number of participants commented on the length of the dwell period. While they considered dwell a reasonable selection method, they felt that 500 ms was too long. Consequently, future work could vary the length of the dwell period to determine if there is an optimal dwell interval for target selection. Alternative selection methods are also possible, for example, using on-screen soft buttons.
CONCLUSIONS
We undertook an empirical and experimental evaluation of tilt as an input primitive for devices with built-in accelerometers, such as touchscreen phones and tablet computers. In a position-select task, participants tilted a tablet computer to maneuver a rolling virtual ball to a destination target. Interaction parameters were manipulated, including tilt gain (25, 50, 100, 200) and selection mode (first-entry, dwell). Results indicate that a tilt gain in the range 50 to 100 is optimal for movement time and throughput. First-entry selection is faster than dwell, and should be used in applications if the interaction allows. Maximum tilt angles ranged from about 2° to 13°, with substantially more tilt used with lower tilt gains. Tilt as an input primitive was shown to conform to Fitts' law, although throughput is low – about half that for a computer mouse.
ACKNOWLEDGEMENT
This research was supported by the Natural Sciences and Engineering Research Council of Canada.
REFERENCES
| 1. | Bartlett, J. F., Rock 'n scroll is here to stay, in IEEE Computer Graphics and Applications, 2000 May/June,
40-45.
|
| 2. | Browne, K. and Anand, C., An empirical evaluation of user interfaces for a mobile video game, Entertainment
Computing, 2011, 1-10.
|
| 3. | Fitts, P. M., The information capacity of the human motor system in controlling the amplitude of movement,
Journal of Experimental Psychology, 47, 1954, 381-391.
|
| 4. | Gilbertson, P., Coulton, P., Chehimi, F., and Vajk, T., Using "tilt" as an interface to control "no-button" 3-D
mobile games, ACM Computers in Entertainment, 6, 2008, 38:1-38:13.
|
| 5. | Harrison, B., Fishkin, K. P., Gujar, A., Mochon, C., and Want, R., Squeeze me, hold me, tilt me! An exploration
of manipulative user interfaces, Proceedings of the ACM SIGCHI Conference on Human Factors in Computing Systems - CHI
'98, (New York: ACM, 1998), 17-24.
|
| 6. | Henrysson, A., Billinghurst, M., and Ollila, M., Virtual object manipulation using a mobile phone, Proceedings of
the International Conference on Augmented Tele-Existence - ICAT '05, (New York: ACM, 2005).
|
| 7. | Henrysson, A., Marshall, J., and Billinghurst, M., Experiments in 3D interaction for mobile phone AR, Proceedings
of the ACM Conference on Computer Graphics and Interactive Techniques in Australia and Southeast Asia - GRAPHITE '07,
(New York: ACM, 2007), 187-194.
|
| 8. | Hinckley, K., Pierce, J., Sinclair, M., and Horvitz, E., Sensing techniques for mobile interaction, Proceedings
of the ACM Symposium on User Interface Software and Technology - UIST 2000, (New York: ACM, 2000), 91-100.
|
| 9. | ISO, Ergonomic requirements for office work with visual display terminals (VDTs) - Part 9: Requirements for
non-keyboard input devices (ISO 9241-9), International Organisation for Standardisation. Report Number ISO/TC 159/SC4/WG3
N147, February 15, 2000.
|
| 10. | MacKenzie, I. S., Kauppinen, T., and Silfverberg, M., Accuracy measures for evaluating computer pointing devices,
Proceedings of the ACM Conference on Human Factors in Computing Systems - CHI 2001, (New York: ACM, 2001), 119-126.
|
| 11. | MacKenzie, I. S., Sellen, A., and Buxton, W., A comparison of input devices in elemental pointing and dragging
tasks, Proceedings of the ACM SIGCHI Conference on Human Factors in Computing Systems - CHI '91, (New York: ACM, 1991),
161-166.
|
| 12. | Partridge, K., Chatterjee, S., Sazawal, V., Borriello, G., and Want, R., TiltType: Accelerometer-supported text
entry for very small devices, Proceedings of the ACM Symposium on User Interface Software and Technology - UIST '02, (New
York: ACM, 2002), 201-204.
|
| 13. | Rekimoto, J., Tilting operations for small screen interfaces, Proceedings of the ACM Symposium on User Interface
Software and Technology - UIST '96, (New York: ACM, 1996), 167-168.
|
| 14. | Sazawal, V., Want, R., and Borriello, G., The unigesture approach, Proceedings of the International Symposium on
Mobile Human-Computer Interaction - MobileHCI '02, (New York: ACM, 2002), 256-270.
|
| 15. | Small, D. and Ishii, H., Design of spatially aware graspable displays, Proceedings of the ACM SIGCHI Conference
on Human Factors in Computing Systems - CHI '97, (New York: ACM, 1997), 367-368.
|
| 16. | Soukoreff, R. W. and MacKenzie, I. S., Towards a standard for pointing device evaluation: Perspectives on 27
years of Fitts' law research in HCI, International Journal of Human-Computer Studies, 61, 2004, 751-789.
|
| 17. | Valente, L., de Souza, C. S., and Feijo, B., Turn off the graphics: designing non-visual interfaces for mobile
phone games, Journal of the Brazilian Computer Society, 15, 2009, 45-58.
|
| 18. | Wang, J., Zhai, S., and Canny, J., Camera phone based motion sensing: interaction techniques, applications and
performance study, Proceedings of the ACM Symposium on User Interface Software and Technology - UIST '06, (New York: ACM,
2006),
101-110.
|
| 19. | Wigdor, D. and Balakrishnan, R., TiltText: Using tilt for text input to mobile phones, Proceedings of the ACM
Symposium on User Interface Software and Technology - UIST 2003, (New York: ACM, 2003), 81-90.
|
| 20. | Zhai, S., Characterizing computer input with Fitts' law parameters: The information and non-information aspects
of pointing, International Journal of Human-Computer Studies, 61, 2004, 791-801.
|
| 21. | Zhai, S., Kong, J., and Ren, X., Speed-accuracy tradeoff in Fitts' law tasks: On the equivalency of actual and nominal pointing precision, International Journal of Human-Computer Studies, 61, 2004, 823-856. |
-----