4. LITERATURE REVIEW AND SURVEYS

A comprehensive review of research using Fitts' law would be a monumental task. A quick tally from the Social Sciences Citation Index between 1970 and 1988 reveals 248 citations of Fitts' 1954 paper. Even this is not fully indicative of the widespread use of Fitts' model since there exists a large body of research in fields such as medicine, sports, and human factors which is published in journals, books, and conference proceedings not surveyed in the SSCI.

This chapter contains four sections, each with a distinct purpose. We begin with a somewhat cursory tour of the huge body of research employing Fitts' law in experimental psychology. This will establish the tremendous generality of the law. Second, results are presented of a re-analysis of the law comparing the Fitts and Shannon formulations for ID. The re-analysis is based on data sets from published Fitts' law research. Third, we focus on several studies and provide an in-depth analysis of the application of Fitts' law in the fields of human factors and human-computer interaction. The analysis highlights the diverse practices employed by researchers in designing experiments and reporting results. As illustrated, these make across-study comparisons difficult because subtle but significant differences are often present. Finally, we examine in detail the study by Gillan et al. (1990), which, at present, is the only application of Fitts' law to dragging tasks.

4.1 The Generality of Fitts' Law

Building upon Fitts' evidence that the rate of human information processing (IP) is constant across a range of task difficulties, other researchers adopted the model to determine IP in settings far removed from Fitts' original theme. It is evident in reviewing the literature that the factors introduced often confound the problem of measurement; numerous studies report vastly different measures for very similar processes.

In a study very similar to Fitts' initial report, Fitts and Peterson (1964) measured IP for a "discrete" task in which subjects responded to a stimulus light and tapped a target on the left or right (see Figure 12).

Figure 12. The discrete paradigm for movement tasks (after Fitts & Peterson, 1964)

In comparison to IP = 10.6 bits/s for "serial" or reciprocal tapping tasks (Fitts, 1954), a rate of 13.5 bits/s was found for discrete tasks (after factoring out reaction time). It is interesting that a difference of 2.9 bits/s surfaced for two tasks which are essentially the same, except for the serial vs. discrete nature of the movements. Others have also found a higher IP for discrete tasks over serial tasks (Megaw, 1975; Sugden, 1980). Keele (1968) suggests that discrete tasks may yield a higher IP because they exclude time-on-target, unlike serial tasks.

The role of visual feedback in controlling the accuracy of movement has been the topic of many experiments using Fitts' law (e.g., Carlton, 1981; Crossman, 1960; Glencross & Barrett, 1983; Keele & Posner, 1968; Kvalseth, 1977; Meyer et al., 1988; Wallace & Newell, 1983). The usual method is to cut off visual feedback a period of time after a movement begins and compare the period of feedback deprivation with changes in accuracy, movement time, or IP. It has been found that movements under approximately 200 ms are ballistic and not controlled by visual feedback mechanisms while those over 200 ms are.

Fitts' law has performed well for a variety of limb and muscle groups. High correlations appear in studies of wrist flexion and rotation (Crossman & Goodeve, 1983; Wright & Meyer, 1983; Meyer et al., 1988), finger manipulation (Langolf et al., 1976), foot tapping (Drury, 1975), arm extension (B. A. Kerr & Langolf, 1977), head movement (Andres & Hartung, 1989a, 1989b; Jagacinski & Monk, 1985), and microscopic movements (W. M. Hancock, Langolf, & Clark, 1973; Langolf & W. M. Hancock, 1975). Underwater experiments have provided a platform for further verification of the model (R. Kerr, 1973; R. Kerr, 1978), as have experiments with mentally retarded patients (Wade, Newell, & Wallace, 1978), patients with Parkinson's disease (Flowers, 1976) or cerebral palsy (Bravo, LeGare, Cook, & Hussey, 1990), the young (Jones, 1989; B. Kerr, 1975; Salmoni, 1983; Salmoni & McIlwain, 1979; Sugden, 1980; Wallace et al., 1978), and the aged (Welford et al., 1969). An across species study verified the model in the movements of monkeys (Brooks, 1979). It has been suggested that the model would hold for the mouth or any other organ for which the necessary degrees of freedom exist and for which a suitable motor task could be devised (Glencross & Barrett, 1989).

Tabulating the results from these reports reveals a tremendous range of performance indices, from less than 1 bit/s (Hartzell, Dunbar, Beveridge, & Cortilla, 1983; Kvalseth, 1977) to over 60 bits/s (Kvalseth, 1981b). Most studies report IP in the range of 3 to 12 bits/s.

4.2 Re-analysis of Published Data

An extensive search of Fitts' law publications was conducted to find summary data that could be re-analysed to compare the Fitts, Welford, and Shannon formulations. Most published research provides results in the form of regression equations, correlations, and/or scatter plots. Summary measures of mean movement times and error rates charted for each A-W condition – as provided by Fitts (see Table 1) – are generally not published.

Of several hundred publications visited, fourteen were found to contain one or more data sets suitable for re-analysis. The data sets were manually converted to machine readable format and were subjected to a correlation analysis of movement time (MT) with each formulation for ID. With only one exception, the Welford formulation yielded a correlation between that obtained using the Fitts and Shannon formulations; therefore the significance test for the difference between the correlations was applied only to the Fitts vs. Shannon combination. The results are shown in Table 4.

Table 4
Re-analysis of Published Data Comparing the Fitts and Shannon Formulation

1st Author and year a	Data set b	ID Range c		Correlations by Model			Higher	Hotelling's t test
		Low	High	Fitts	Shannon	Inter-Model		t	n	p
Andres, 1989	a	2.0	5.6	.9661	.9757	.9986	Shannon	2.81	9	.05
	b	2.0	5.6	.9767	.9789	.9986	Shannon	0.49	9	-
	t	2.0	5.6	.9762	.9822	.9986	Shannon	1.66	9	-
Annett, 1958	a	4.0	10.0	.9887	.9871	.9999	Fitts	1.07	4	-
	b	4.0	10.0	.9980	.9974	.9999	Fitts	0.74	4	-
	c	4.0	10.0	.9933	.9919	.9999	Fitts	1.62	4	-
	t	4.0	10.0	.8909	.8852	.9999	Fitts	1.87	4	-
Drury, 1975		0.9	3.3	.9602	.9749	.9971	Shannon	3.74	12	.01
Gan,1988		1.0	6.0	.8113	.8359	.9964	Shannon	3.62	40	.001
Glencross, 1983	a	1.0	6.6	.9737	.9871	.9965	Shannon	5.39	16	.01
	b	1.0	6.6	.7850	.7795	.9965	Fitts	0.38	16	-
Kerr, 1973	a	3.6	7.2	.9926	.9926	.9998	Fitts	0.05	9	-
	b	3.6	7.2	.9869	.9878	.9998	Shannon	0.69	9	-
	t	3.6	7.2	.9944	.9949	.9998	Shannon	0.57	9	-
Kerr,1977a		3.0	7.3	.6859	.6865	.9997	Shannon	0.11	16	-
Kerr, 1978	a	2.7	8.0	.9974	.9959	.9994	Fitts	1.64	9	-
	b	2.7	8.0	.9884	.9871	.9994	Fitts	0.59	9	-
Kerr, 1977b		3.0	7.3	.9622	.9650	.9997	Shannon	1.63	16	-
Kvalseth, 1976		1.6	6.6	.9870	.9861	.9979	Fitts	0.26	12	-
Kvalseth, 1977		2.6	7.6	.6353	.6313	.9993	Fitts	0.43	12	-
MacKenzie, 1987		2.6	7.6	.9792	.9822	.9993	Shannon	1.40	12	-
Marteniuk, 1987	a	2.0	5.6	.9809	.9877	.9986	Shannon	0.33	4	-
	b	3.3	5.53	.8545	.8557	.9997	Shannon	0.10	4	-
Sugden, 1980	a	2.0	5.6	.9809	.9877	.9986	Shannon	2.24	7	-
	b	3.0	5.6	.9889	.9859	.9997	Fitts	1.84	6	-
a see Appendix A for data sets and complete references b a, b, c = data set; t = aggregate data c computed using Fitts' formulation d two-tailed text, df = n - 3

Of the 25 data sets (rows) in Table 4, the MT-ID correlation was higher 14 times using the Shannon formulation vs. the Fitts formulation. Of these, the difference between the correlations was statistically significant at the p < .05 level (or better) four times. Of the eleven data sets in which the Fitts formulation correlated higher, statistical significance was never achieved.

It is worthwhile examining the range of task conditions employed. As noted earlier, the models differ dramatically only when task conditions include low values of ID (see Figure 3). The mean of the low values for ID (third column in the table) is 2.7 bits. Of the cases in which the Fitts or Shannon correlations were higher, the means were 3.0 bits and 2.4 bits respectively. Thus, the anticipated trend of higher correlations using the Shannon model appearing when experimental conditions include low extremes of task ID is present in the table.

The difference in the correlations in the experiment by Gan and Hoffmann (1988) achieved significance at the p < .001 level. This is largely due to the range of conditions employed. A and ID were considered independent variables (as opposed to A and W, as typical) and were varied over 4 and 10 levels each. (The W value was adjusted as necessary to meet the desired levels for ID across each level of A.) ID levels were 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, and 6 bits; thus, there were four conditions of ID = 1 bit, four conditions of ID = 1.5 bits, and so on. Since low values of ID were well represented, it is not surprising that a dramatic difference between the models (t = 3.62, df = 37, p < .001) surfaced in this experiment.

In summary, the re-analysis of published data presented in Table 4 provides further support that the Shannon formulation is empirically superior to the Fitts formulation, although the improvement is slight.

4.3 Human Factors and Human-Computer Interaction

Despite the large body of research evaluating the performance of computer input devices for a variety of user tasks, the discipline of human-computer interaction has not, as a rule, been a proving ground for Fitts' law performance models. Most related HCI research uses "task completion time" as the unit of study, with errors or other measures reported in separate analyses. Two-factor repeated measures experiments with several levels each for "task" and "device" are the norm (e.g., Albert, 1982; Buxton & Myers, 1986; English, Engelbart, & Berman, 1967; Ewing, Mehrabanzad, Sheck, Ostroff, & Shneiderman, 1986; Goodwin, 1975; Gould, Lewis, & Barnes, 1985; Haller, Mutschler, & Voss, 1984; Karat, McDonald, & Anderson, 1984; Mehr & Mehr, 1972; Sperling & Tullis, 1988). See Greenstein and Arnaut (1988), Milner (1988), or Thomas and Milan (1987) for reviews of this body of research.

Six Fitts' law studies have been selected as relevant to the present discussion. These are surveyed in reference list order, focusing initially on the methodology and empirical results. An assessment of the findings within and across studies is deferred to the end.

4.3.1 Card, English, and Burr, 1978

This highly cited work stands apart from other investigations by nature of its goal to transcend the simplistic ranking of devices, and to develop "models" useful for subsequent device evaluations. The idea is that once a model is derived, it can participate in subsequent designs by predicting performance in different scenarios before design is begun.

Selection time, error rates, and learning time were measured in a routine text selection task using four devices: a mouse, an isometric joystick, step keys, and text keys. The step keys moved the cursor up, down, left, or right in the usual way, whereas the text keys advanced the cursor on character, word, or paragraph boundaries. The joystick controlled the velocity and direction of the cursor from the magnitude and direction of the applied force, with negligible displacement of the stick.

For each trial, subjects pressed the space bar, "homed" their hand on the cursor-control device, advanced the cursor to a word highlighted in a block of text, then selected the word by pressing a button or key. Experimental factors were device (four levels), distance to target (A = 1, 2, 4, 8, & 16 cm), target size (W = 1, 2, 4, & 10 characters; 1 character = 0.246 cm), approach angle (0-22.5° , 22.5-67.5° , & 67.5-90° ), and trial block. IDs ranged from -0.14 bits (A = 1 cm, W = 10 characters) to 6.0 bits (A = 10 cm, W = 1 character). (The negative index is discussed later.) Target height was held constant at 0.456 cm, the height of each character.

Using Welford's variation of Fitts' law, prediction equations were derived for the two continuous devices. The least-squares regression equation predicting movement time (ms) for the mouse was

MT = 1030 + 96 ID,

(17)

with IP = 10.4 bits/s (r = .91, SE = 70 ms), and for the joystick,

MT = 990 + 220 ID,

(18)

with IP = 4.5 bits/s (r = .94, SE = 130 ms).

Mean movement time was lowest for the mouse (1660 ms, SD = 480 ms) despite the fact that mean homing time was highest (360 ms, SD = 130 ms). The joystick was a close second (MT = 1830 ms, SD = 570 ms), followed by the text keys (MT = 2260 ms, SD = 1700 ms) and step keys (MT = 2510 ms, SD = 1640 ms).

Error rates ranged from 5% for the mouse to 13% for the step keys. Approach angle did not affect mean movement time for the mouse, but increased movement time by 3% for the joystick when approaching a target along the diagonal axis.

4.3.2 Drury, 1975

Welford's variation of Fitts' law was evaluated as a performance model in a study of foot pedal design. Using their preferred foot, subjects tapped back and forth between two pedals for 15 cycles (30 taps). Six different amplitudes (A = 150, 225, 300, 375, 525, & 675 mm) were crossed with two pedal sizes (W = 25 & 50 mm). The mean width of subjects' shoes (108.8 mm) was added to target width as a reasonable adjustment since any portion of a shoe touching the target was recorded as a hit. As such, IDs ranged from 0.53 to 2.47 bits. With A = 150 mm and W = 50 + 108.8 = 158.8 mm, the task difficulty was calculated as log₂(150.0 / 158.8 + 0.5) = 0.53 bits. This is an extremely relevant example of a task condition in which an index of difficulty less than 1 bit is perfectly reasonable. In effect, the targets were overlapping.

The correlation between MT and ID was high (r = .970, p < .01) with regression line coefficients of 187 ms for the intercept and 85 ms/bit for the slope (IP = 11.8 bits/s).

Overall error rates were not reported; but blocks with more than one miss were repeated. Thus, by design the error rate was less than 3.3%.

4.3.3 Epps, 1986

Six cursor control devices were compared in a target selection task with performance models derived using Fitts' law, a power model (Equation 13), and the following first-order model proposed by Jagacinski, Repperger, Ward, and Moran (1980):

MT = a + b × A + c × (1 / W − 1).

(19)

Device types included two touchpads (relative & displacement), a trackball, two joysticks (displacement & force; both velocity-control), and a mouse. For each trial subjects moved a cross-hair tracker to a randomly positioned rectangular target and selected the target by pressing a button. Target distance varied across four levels (A = 2, 4, 8, & 16 cm) and target size across five levels (W = 0.13, 0.27, 0.54, 1.07, & 2.14 cm), yielding IDs from 0.90 to 6.94 bits.

The power model provided the highest (multiple) correlation with MT across all devices, with the first-order model providing higher correlations for some devices but not others. The correlations throughout were low, however, in comparison to those usually found. Using Fitts' equation, r ranged from .70 for the relative touchpad to .93 for the trackball. Intercepts varied from -587 ms (force joystick) to 282 ms (trackball). The values for IP, ranging from 1.1 bits/s (displacement joystick) to 2.9 bits/s (trackball), are among the lowest to appear in Fitts' law experiments.

If an error was committed, subjects had to reposition the cursor inside the target and press the select button again. Although the frequency of this behaviour was not noted, presumably these trials were entered using the total time for the operation.

4.3.4 Jagacinski and Monk, 1985

Fitts' law was applied to a target acquisition task using a displacement joystick for position control and a head-mounted sight using two rotating infrared beams. Each trial began with the cursor in the middle of the display and the appearance of a circular target on the screen. Subjects moved the cursor to the target and selected it. On-target dwell time (344 ms), rather than a button push, was the criterion for target selection.

Experimental factors were device (two levels), target distance (A = 2.45, 4.28, & 7.50 degrees of visual angle), target size (W = 0.30, 0.52, & 0.92 degrees for the joystick; W = 0.40, 0.70, & 1.22 degrees for the helmet-mounted sight), and approach angle (0, 45, 90, 135, 180, 225, 270, & 315 degrees). Task difficulties ranged from 2.0 to 5.6 bits for the helmet-mounted sight. Correlations between MT and ID were very high (r = .99) for both devices with regression coefficients for the intercept of −268 ms (helmet-mounted sight) and −303 ms (joystick). The regression line slope for both devices was 199 ms/bit (IP = 5 bits/s). Mean movement times were slightly longer along the diagonal axes for the joystick (7.2%) and for the helmet-mounted sight (9.1%). Since the selection criterion was dwell time inside the target, errors could not occur.

4.3.5 Kantowitz and Elvers, 1988

Fitts' law was evaluated as a performance model for two isometric joysticks, one for cursor position control, the other for cursor velocity control. Each trial began with the appearance of a square target in the centre of the screen and an asterisk pre-cursor on either side which tracked the applied force of the joystick. When the pre-cursor changed to a cross-hair cursor, the subject moved it to the target and selected the target. A trial terminated after one of the following: the cursor remained stationary (±3 pixels) for 333 ms, the horizontal direction of movement changed, or 4 s elapsed timeout. Experimental factors were device (two levels), target distance (A = 170, 226, & 339 pixels), target size (W = 20 & 30 pixels), and C-D gain (high & low). Four target distance/size combinations were chosen with IDs from 3.5 to 5.5 bits.

The velocity-control joystick regression line had a steeper slope, and therefore a lower IP, than for the position-control joystick (IP = 2.2 bits/s vs 3.4 bits/s). There was no main effect for C-D gain; for each device, the high and low gain regression lines were parallel. The intercepts, however, were large and negative. Under high gain and low gain conditions respectively, intercepts were −328 and −447 ms under position control and −846 and −880 ms under velocity control. Correlations ranged from .62 to .85. The average error rate was very high (around 25%), although figures were not provided across factors.

4.3.6 Ware and Mikaelian, 1987

Welford's variation of Fitts' law was applied to positioning data from a selection task using an eye tracker (Gulf and Western series 1900). A cross-hair cursor positioned on a CRT display was controlled by the reflection from subjects' cornea of an infrared source. Targets were selected by three methods: a hardware button, dwell time on target (400 ms), and an on-screen button. Seven rectangles (3.2 by 2.6 cm) were presented to the subjects in a vertical row. After fixating on the centre rectangle for 0.5 s, one of the seven became highlighted, whereupon subjects immediately fixated on it and selected it.

The application of Fitts' law in this study is weak. Target size was kept constant (2.6 cm) while distance was varied over four levels (0, 2.6, 5.2, & 7.8 cm). Although IDs ranged from −1.0 bit to 1.8 bits, no rationale was provided for the negative index at A = 0 cm, calculated as log₂(0 / 2.6 + 0.5) = −1 bit. Correlations and regression coefficients were omitted in lieu of a scatter plot of MT vs. ID with regression lines for each selection technique. For the purpose of this survey, equations were inferred from the plots. Intercepts ranged from 680 to 790 ms and slopes ranged from 73 to 107 ms/bit. The highest IP was for the hardware button condition (13.7 bits/s) and the lowest was for dwell time (9.3 bits/s).

Error rates were high, ranging from 8.5% (hardware button) to 22% (on-screen button). As the investigators noted, an eye-tracker can provide fast cursor positioning and target selection, as long as accuracy demands are minimal.

4.4 Across-Study Comparison of Performance Measures

We now proceed with the task of assessing the findings and comparing them across studies. Table 5 shows for each device condition the regression coefficients, the MT-ID correlation, and the percentage errors. Both the slope and IP are provided for convenience, as are the values from Fitts' (1954) tapping experiment with a 1 oz stylus (see Table 2). The entries are ordered by decreasing IP. This is not the same as ordering by increasing movement time since the intercepts also contribute to MT. It is felt that IP is more indicative of the overall performance of a device and that normalizing the intercepts is reasonable for this comparison.

The presence of nine negative intercepts in Table 5 is the first sign of trouble. A negative intercept implies that, as tasks get easier, a point is reached where the predicted movement time is negative. This, of course, is nonsense and indicates a flaw in the application of the model or the presence of uncontrolled variations in the data. Beyond this, the most notable observation is the overall lack of consensus in the measures. The spread of values is astonishing: Performance indices ranged from 1.1 to 13.7 bits/s, intercepts ranged from -880 to 1030 ms. Are these a true reflection of innate differences in the devices? Probably not. Although differences are expected across devices, similar measures should emerge in the table where different entries are for the same device.

For example, the mouse was evaluated by Card et al. (1978) and Epps (1986). The former cite IP = 10.4 bits/s while the latter cites IP = 2.6 bits/s. These values differ by a factor of four! Also, the intercepts differ by 922 ms. So, what is the Fitts' law prediction equation for the mouse? The answer is up for debate.

Also, an isometric, velocity-control joystick was tested by Card et al. (1978), Epps (1986), and Kantowitz and Elvers (1988). Again, the outcome is disturbing. In the order just cited, the intercepts were reported as 990, −587, and 863 ms (average), and IP was reported as 4.5, 1.2, and 2.2 bits/s. It seems the goal cited earlier — to develop models for evaluating devices and interaction techniques prior to implementation — remains elusive.

4.5 Sources of Variation

We can attempt to reconcile the differences by searching out the major sources of variation. Indeed, some of these are nascent traits of direct manipulation systems (rather than quirks in methodology), and, therefore, are particularly pertinent to the context of human-computer interaction. Identifying these provides a basis for evaluating and comparing studies. When disparities emerge it may be possible to adjust measures or to predict comparative outcomes under hypothetical circumstances.

4.5.1 Device Differences

If the research goal is to establish a Fitts' law (or other) performance model for two or more input devices, then the only source of variation that is desirable is the between-device differences. This is what the investigations are attempting to measure. Accomplishing this assumes, somewhat unrealistically, that all other sources of variation are removed or are controlled for. Of course, very few studies are solely interested in device differences. "Sources of variation" become "factors" in many studies — equally as important to the research as model-fitting across devices.

We can cope with the disparity in Table 5 by looking for across-study agreement on within-study ranking rather than comparing absolute measures. The mice and velocity-control isometric joysticks evaluated by Card et al. (1978) and Epps (1986) provide a simple example. The index of performance was higher for the mouse than for the joystick within each study. One could conclude, therefore, that the mouse is a better performer (using IP as the criterion) than the joystick, even though the absolute values are deceiving. (Note that the joystick in Card et al.'s study yielded a higher IP than the mouse in Epps' study.) Furthermore, the differences between devices expressed as a ratio was about the same: IP was higher for the mouse than for the joystick by a factor of 10.4 / 4.5 = 2.3 in Card et al.'s (1978) study and by a factor of 2.6 / 1.2 = 2.2 in Epps' (1986) study.

Just as the units disappear when the ratio of the performance indices is formed, so too may systematic effects from other sources of variation, including a myriad of unknown or uncontrolled factors present in an experiment. Indeed, "experiment" differences are evident in Table 5: Epps' (1986) and Kantowitz and Elvers' (1988) studies have "low" values for IP; Card et al.'s (1978) and Drury's (1975) studies have "high" values. Thus, relative differences within studies gain strength if across-study consensus can be found.

A larger sample of studies would no doubt reveal within-study consensus on other performance differences. The performance increment found in Kantowitz and Elvers' (1988) study for the position-control joystick over the velocity-control joystick, to cite one example, was noted in another study not in the survey (Jagacinski, Repperger, Moran, Ward, and Glass, 1980).

We should acknowledge as performance determinants the range of muscle and limb groups engaged by different manipulanda. Since smaller limb groups (e.g., wrist vs. arm) have shown higher ratings for IP (Langolf et al., 1976), performance increments are reasonable when complex arm movements are avoided. With fewer degrees of freedom for the head or eyes than for the arm, the relatively high rates for the eye tracker and helmet-mounted sight in Table 5 may be warranted. This does not, however, account for the high ranking of the foot pedals.

It is felt that Fitts' law performance differences can be attributed to other characteristics of devices, such as number of spatial dimensions sensed (1, 2, or 3), or property sensed (pressure, motion, or position); however, our sample is too small to form a basis for generalization. Besides, the studies surveyed may contain stronger sources of variation.

4.5.2 Task Differences

It is naive, perhaps, to suggest that there exists a generic task which can accommodate simple adjustments for other factors, such as "device". One might argue that Fitts' tapping task is remote and inappropriate: It is not a particularly common example of user interaction with computers. Its one dimensional simplicity, however, has advantages for model building, not the least of which is access to a substantial body of research. For example, there is evidence that a serial task yields an index of performance 2 to 3 bits/s lower than a similar discrete task (e.g., Fitts & Peterson, 1964). Discrete tasks may be more akin to direct manipulation systems, but experiments are easier to design and conduct using a serial task. Knowledge of a 2 to 3 bit per second increment for discrete operation after conducting a serial task experiment is a valuable resource for researchers.

Of the six studies surveyed, all but one used a discrete task. Drury's (1975) serial foot tapping experiment yielded IP = 11.8 bits/s, but may have shown a rate around 14 bits/s had a discrete task been used. Although this would tend to disperse further the rates in Table 5, indices in the 15 to 20 bits/s range are not uncommon in Fitts' law studies.

Five of the six studies used a simple target capture task while one, Card et al. (1978), used a text selection task. The cognitive load on subjects may have been higher in the latter case due to the presence of additional text on the screen. Perhaps the burden of finding and keeping track of highlighted text within a full screen of text continued throughout the move. This "task difference" would reduce performance but one can only speculate on where the effect would appear. The evidence leans toward the intercept since they were highest in this study (1030 & 990 ms).

4.5.3 Selection Technique

The method of terminating tasks deserves separate analysis from other aspects of tasks. In the studies by Card et al. (1978) and Epps (1986), the target selection button for all devices except the mouse was operated with the opposite hand. Ware and Mikaelian (1987) also used a separate hand-operated button as one of the selection conditions with the eye tracker. There is evidence that task completion times are reduced when a task is split over two hands (e.g., Buxton & Myers, 1986), suggesting that parallel cognitive strategies may emerge when positioning and selecting are delegated to separate limbs. This may explain the trackball's higher IP over the mouse in Epps' (1986) experiment – the mouse task was one-handed, the trackball task was two-handed. Unfortunately, this speculation does not extend to Card et al.'s (1978) study where IP was significantly higher for the mouse (one-handed) than for the joystick (two-handed).

Conversely, and as mentioned earlier, target selection time may be additive in the model, contributing to the intercept of the regression line, but not to the slope. This argument has some support in Epps' (1986) study where the intercept is second highest out of five for the mouse. Both the mouse and the joystick yielded similar intercepts in Card et al.'s (1978) study, thus lending no support either way.

There are presently versions of each device that permit manipulation and target selection with the same limb. Therefore, a "devices" by "mode of selection" experiment could examine these effects on the intercept and slope in the prediction equation. In fact, mode of selection was a factor in Ware and Mikaelian's (1987) study. Based on this study, one would conclude that IP increases when selection is delegated to a separated limb (as it did for the hardware button condition vs. the dwell time or on-screen button conditions; see Table 5).

4.5.4 Range of Conditions and Choice of Model

In Fitts' (1954) tapping experiments, subjects were tested over four levels each for target amplitude and target width with the lowest value for target amplitude equal to the highest value for target width (see Table 1). In all, subjects were exposed to sixteen A-W conditions with IDs from 1 to 7 bits. Table 6 shows the range of target conditions employed in the studies surveyed.

Some stark comparisons are found in Table 6. Kantowitz and Elvers (1988) and Ware and Mikaelian (1987) limited testing to four A-W conditions over a very narrow range of IDs (2.00 bits and 2.80 bits, respectively). Although Drury (1975) used 12 A-W conditions, the range of IDs was only 1.94 bits. This resulted because the spreads for A and W were small. Despite using 6 levels for A, the ratio of the highest value to the lowest value was only 4.5, and the same ratio for W was only 1.2. (When a scatter plot is limited to a very narrow range, one can imagine a line through the points tilting to and fro with a somewhat unstable slope!) The narrow range of IDs in Kantowitz and Elvers' (1988) study, combined with the observation that the lowest ID was very high (3.50 bits), could explain the large negative intercepts. (After travelling 3.5 bits to the origin, a line swivelling about a narrow cluster of points could severely miss its mark!) Note that the predicted movement time when ID = 1 bit with Kantowitz and Elvers' (1988) velocity-control joystick under low-gain conditions is 449(1) − 880 = −431 ms. Although ID = 1 bit is not unreasonable (e.g., see Table 1), a negative prediction for movement time is. Had this experiment included a wider range of IDs, extending down to around 1 bit, no doubt the regression line intercepts would be higher and the slopes would be lower.

Card et al. (1978) and Epps (1986) used a reasonable number of conditions (20 & 9, respectively) over a wide range of task difficulties (6.18 & 6.04 bits). These represent a strong complement of conditions which should yield results bearing close scrutiny.

Although a non-zero intercept can be rationalized a variety of ways, the studies by Card et al. (1978) and Ware and Mikaelian (1987) present a special problem. In these, IDs < 0 bits represent conditions that actually occurred; thus, it is certain that an appreciable positive intercept results. A contributing factor in the Card et al. (1978) study is the confounding approach angle (discussed below). In both studies, however, the negative IDs would disappear simply by using Shannon's formulation for ID (Equation 9). This would reduce the regression line intercepts because the origin would occur left of the tested range of IDs (where it should) rather than in the middle.

It is also possible that Fitts' law is simply the wrong model in some instances. Card et al. (1978) noted in the scatter plot for the joystick a series of parallel lines for each target amplitude condition. Certainly, this is not predicted in the model: A and W play equal but inverse roles; and, at a given ID, only random effects should differentiate the outcomes. Noting the systematic effect of amplitude, separate prediction equations were devised for each value of A. The result was a series of parallel regression lines with slopes around 100 ms/bit (IP = 10 bit/s) and with intercepts falling as A decreased. With this adjustment, the joystick and mouse IPs were about the same. However, this is a peculiar situation for the model – in essence, target amplitude ceases to participate.

The range of conditions also bears heavily on the coefficient of correlation. Although r is extremely useful for comparisons within a study, across-study comparisons are all but impossible unless the conditions are the same. As noted earlier, correlations are uncharacteristically low when a sample is drawn from a restricted range in a population. This could explain the relatively low correlations in Table 5 for Kantowitz and Elvers' (1988) study.

The extent of data aggregation also affects r. In the vast majority of Fitts' law studies, movement times are averaged across subjects and a single data point is entered into the analysis for each A-W condition. Epps (1986) did not average across subjects and entered 240 data points into the analysis (12 subjects × 5 amplitudes × 4 widths). The extra variation introduced may be the cause of the relatively low correlations in this study.

4.5.5 Approach Angle and Target Width

In the Card et al. (1978) study the use of approach angle as an experimental factor in conjunction with the consistent use of wide, short targets (viz., words) provides the opportunity to address directly a theoretical point raised earlier: What is "target width" when the approach angle varies?

When target distance was 1 cm and target width was 10 characters (2.46 cm), the index of difficulty was calculated in this study using Welford's formulation as log₂(A / W + 0.5) = log₂(1 / 2.46 + 0.5) = −0.14 bits. This troublesome value, although not explicitly cited, appeared in the scatter plot of MT vs. ID (Figure 6, p. 609). Since character height was 0.456 cm, a better measure of ID may have been log₂(1 / 0.456 + 0.5) = 1.43 bits. With a slope of 96 ms/bit for the mouse regression line, this disparity in IDs increases the intercept by as much as (1.43 − (−0.14)) × 96 = 151 ms. The contribution could be even more in a regression analysis using We since adjusting target width generally increases the regression line slope and increases ID for easy tasks (cf. Figure 2 & Figure 5).

Thus, the negative IDs and the very large intercepts in the Card et al. (1978) study are at least partially attributable to the one-dimensional limitations in the model and to the use of a formulation for ID which allows for a negative index of task difficulty. As the investigators noted, however, the time spent in grasping the device at the beginning of a move and the time for the final button-push were also contributing factors.

Epps (1986) and Jagacinski and Monk (1985) also varied approach angle. Since the targets were squares or circles, however, there is no obvious implication to the calculation of task difficulty or to the regression coefficients.

4.5.6 Error Handling

Response variability (viz., errors) is an integral part of rapid, aimed movements. Unfortunately, the role of "accuracy" is often neglected in the application of Fitts' law. Jagacinski (1989) notes the following:

It is difficult to reach any conclusions when one system has exhibited faster target acquisitions, but has done so with less accuracy in comparison with another system. Both systems might have the same speed-accuracy function, and the experimental evaluation might have simply sampled different points along this common function. (p. 139)

A simple way out of this dilemma is to build the model using the effective target width (W_e) in the calculation of ID. The adjustment normalizes target width for a nominal error rate of 4%, as described earlier. However, none of the studies surveyed included the adjustment. Unfortunately, post hoc adjustments cannot be pursued at this time because error rates across levels of A and W were not reported. Although speculation is avoided on possible adjustments to the regression coefficients, it is instructive to review the strategies adopted for error handling.

Card et al. (1978) excluded error trials from the data analysis. Drury (1975) included error blocks in the data analysis provided at most 1 miss in 30 trials was committed. Although Kantowitz and Elvers (1988) and Ware and Mikaelian (1987) reported very high error rates (up to 25%), it was not stated if error trials were included in the regression analyses. Presumably they were.

In Kantowitz and Elvers' (1988) study, subjects were not allowed to reverse the horizontal direction of movement. If a reversal was detected the trial immediately terminated and a miss was recorded if the cursor was outside the target. This precludes potential accuracy adjustments at the end of a trial, which, no doubt, would increase movement time.

Jagacinski and Monk (1985) and Epps (1986) introduced selection criteria whereby errors could not occur — a trial continued until the target was captured. If the cursor was outside the target when the select button was pressed, subjects in Epps' (1986) study repositioned the cursor and re-selected the target. Although the frequency was not reported, the inclusion of trials exhibiting such behaviour is most unusual.

4.5.7 Learning Effects

Learning effects are a nagging, ubiquitous source of variation in experiments that seek to evaluate "expert" behaviour. Often research pragmatics prevent practicing subjects up to expert status. Fortunately though, Fitts' serial or discrete paradigm is extremely simple and good performance levels are readily achieved. Of the six studies surveyed, three made no attempt to accommodate learning effects. Of those that did, each used a different criterion to establish when asymptotic, or expert, levels were reached. The most accepted statistical tool for this is a multiple comparisons test (e.g., Newman-Keuls, Scheffé, Tukey) on mean scores over multiple sessions of testing (Glass & Hopkins, 1984, chap. 17).

Only Epps (1986) included such a test. Although the design was fully within-subjects, only two hours of testing were needed for each subject. This was sufficient to cross all levels of device (six), session (five), amplitude (four), and width (five). Subjects were novices and were given only two repetitions of each experimental condition; yet a multiple comparisons test (Bonferroni's t test; see Glass and Hopkins, 1984, p. 381) showed no improvement overall or for any device after the second session. The data analysis was based on sessions three to five.

Jagacinski and Monk (1985), who practiced subjects for up to 29 days, used the criterion of four successive days with the block means on each day within 3.5% of the four-day mean. Card et al. (1978) developed a similar criterion based on a t test.

4.5.8 Summary

Other potential sources of variation abound. These include the instructions to subjects, the number of repetitions per condition, the order of administering devices, the sensitivity of device transducers, the resolution and sampling rate of the measuring system, the update rate of the output display, and control-display gain. However, our analysis will not extend further. The discussions on error handling and learning effects highlighted the vastly different strategies employed by researchers; but speculating on the effect of these in the model is digressive. These and other sources are felt to introduce considerable variation, but with effects which are, for the most part, random. Systematic effects may be slight, unanticipated, or peculiar to one design.

The range of conditions selected at the experimental design stage is a major source of variation in results. Experiments can benefit by adopting a wide and representative range of A-W conditions (e.g., 1 to 7 bits; see Table 1). This done, the investigators can proceed to build valid information processing models when other factors such as "device" or "task" are added. Adopting the Fitts paradigm for serial tasks (Figure 1) or discrete tasks (Figure 12) offers the benefit of a simple experimental setup and invites access to a large body of past research.

Experiments that vary approach angle and use rectangular or other "long and narrow" targets can avoid the problem of negative task difficulty by using the Shannon formulation of Fitts' law (Equation 9, Figure 3) and/or adopting a new notion of target width in the calculation of ID (Figure 7). Extending the model to accommodate varying approach angles and target shapes is one area in need of further research, particularly in light of the two-dimensional nature of user input tasks on computers.

The variety of schemes to terminate tasks and select or acquire a target undoubtedly affects the outcome of a regression analysis. There are reasonable grounds for expecting a distinct, additive component to appear in the intercept; however, evidence is scant and inconclusive. Further research is needed.

A major deficiency in the application of Fitts' law in general is the absence of a sound and consistent technique for dealing with errors. Although not demonstrated in any of the studies surveyed, the model can be strengthened using the effective target width in calculating ID (Figure 4). Doing so normalizes response variability (viz., errors) for a nominal error rate of 4%. This theoretically sound (and arguably vital) adjustment delivers consistency and facilitates across-study comparisons. The adjustment can proceed using the error rate or the standard deviation in end-point coordinates, as shown earlier.

Experiments are strengthened by practicing subjects until a reasonable criterion for expert performance is met. The three studies that tested for learning effects did so using mean movement times. It may be more appropriate, however, to also test subjects' "rate of information processing" (viz., IP) as a criterion variable. This test could be strengthened using W_e in the calculation of ID (see Table 1) to accommodate both the speed and accuracy of performance. The direct method of calculating IP (viz., IP = ID / MT ; see Table 1) is easier and probably better since it nulls the intercept, blending the effects into IP. This would accommodate separate, distinct learning effects for the intercept which would be unaccounted for if IP = 1 / b (from a regression analysis) is used.

The prediction equations in the Fitts' law studies surveyed reveal large inconsistencies, making it difficult to summarize and offer de facto standard prediction equations for any of the devices tested. Despite high correlations (usually taken as evidence of a model's worth), the failings in across-study comparisons demonstrate that extracting a Fitts' law prediction equation out of a research paper and embedding it in a design tool may be premature as yet.

4.6 Fitts' Law in Dragging Tasks

The study by Gillan et al. (1990) is at present the only study to extend Fitts' law to dragging tasks and to explore alternative measures for target width. Since the results are of particular relevance to the present research, a separate, detailed review is warranted.

Two experiments were described, both employing the same task but under slightly different conditions. Two tasks were employed: point-select and point-drag-select. In the point-select task, subjects moved the cursor to a block of highlighted text and selected it by pressing and releasing the mouse button. In the point-drag-select task, subjects selected the left character in a block of text with a button-down action, then "dragged" through to the right-most character and terminated the move with a button-up action. Factors in the first experiment were task (two levels), distance to target (A = 2, 7, 5, & 13,75 cm), and width of target (W = 1, 5, 14, & 26 characters; 1 character ≈ 0.25 cm). The height of targets was held constant at 0.5 cm, the height of each character. Although each of the four diagonal angles was used as a direction of movement, approach angle was not analysed as a factor. The intent in Gillan et al.'s (1990) study was to establish the appropriate target width to use in models for pointing tasks and dragging tasks.

Some unusual and puzzling views of the data were presented. For example, in the point-drag-select task they built a Fitts' law model with pointing time as the predicted variable and Welford's ID as the controlled variable. ID was calculated using pointing distance as A and dragging distance as W. This is counter-intuitive. Since pointing ends when dragging begins, there is no reasonable ground to expect dragging distance to serve as W in a model for pointing time. It is not surprising that the model yielded a very low r of .50 (p. 230).

Nevertheless, there are some valuable results found in this study. In the point-select task, a "status quo" Fitts' law model was compared with a variation that replaced target width with the constant 0.5 cm, corresponding to the height of words. Using Welford's formulation they found

MT = 795 + 83 log2(A / W + 0.5) ms

(20)

with r = .75 using the status quo model, and

MT = 497 + 180 log2(A / 0.5 + 0.5) ms

(21)

with r = .94 using a constant for target width (p. 230). Initially, it appears odd that the model with an extra free variable was outperformed by the model substituting a constant (r = .75 vs. r = .94); but this is perfectly reasonable both in a statistical sense and in a pragmatic sense. Statistically, if A and W were separate variables participating in a multiple regression model, it is certain that W, as a free variable (with its own regression coefficient), would improve the correlation of the model in comparison to a model substituting a constant for W. However, this is not the case with Fitts' law since A and W combine to form Fitts' index of difficulty in a one-variable regression model. Each variable taken alone does not necessarily improve the correlation of the model.

In a pragmatic sense, the lower correlation found using the status quo model is better understood by examining Figure 13, taken from Gillan et al.'s (1990) report (p. 229). For each amplitude condition, pointing time was longer for the W = 1 character = 0.25 cm condition than for the W = 5, 14, or 26 character conditions. However, there was no apparent change in movement time over the larger three target width conditions. This, of course, is not predicted in Fitts' model. A higher r would have resulted for the status quo model only if decreases in movement time were found as W increased, as consistent with the relative roles of W and A in Fitts' index of difficulty.

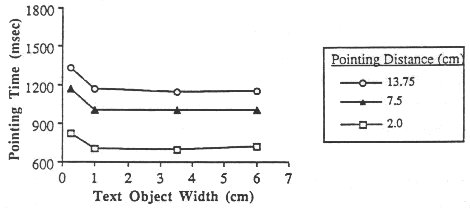
Figure 13. Pointing time vs. A and W (from Gillan et al., 1990)

The improved correlation found when substituting a constant equal to the height of the characters lends support to the "smaller-of" theory mentioned earlier (see p. 29). Since words are short and wide, the height of the words may be a more appropriate measure of the precision requirement of the task, and may better serve the role of target width in the model. Furthermore, had a smaller-of model been used in Gillan et al.'s (1990) analysis, target width would have been assigned the value 0.25 cm (the width of a single character) when W = 1 character and the value 0.5 cm (the height of characters) when W = 5, 14, and 26 characters. The extra time taken to select single-character targets (see Figure 13), in conjunction with the similarity in times to select the 5, 14, and 26 character targets, raises the possibility that the smaller-of model might have outperformed the model using W = 0.5 cm for all target widths.

Gillan et al. (1990) did build a model for the dragging operations (although it is mentioned in a subordinate way and not featured in their tables). They found movement time (ms) during dragging was well expressed (r = .99) by

MT = 684 + 328 log2(A / 0.5 + 0.5),

(22)

which suggests an information processing rate of IP = 3.0 bit/s. (The variable A in this model corresponds to the dragging distance.) The constant 0.5 cm was again substituted for target width. Since the height of characters is measured perpendicular to the line of motion in dragging tasks, the substitution is of questionable merit. The width of a single character (0.25 cm), corresponding to the width of the region where the terminating button- up action occurred, may be a better choice.

Since substituting a constant equal to the height of words for target width served well in the first experiment, Gillan et al. (1990) varied the height of words in the next experiment. Factors were task, pointing distance (A = 2.5, 7.0, & 11.75 cm), target width (W = 1.0, 3.5, & 6.0 cm), and target height (H = 0.4, 0.5, & 1.2 cm). Again, the direction of movement varied but was not included in the analysis.

For the point-drag-select task, two models for dragging time were tested, one using the constant 0.5 cm for target width, and one using H for target width. In the former case, movement time (ms) while dragging was predicted as

MT = 594 + 349 log2(A / 0.5 + 0.5)

(23)

with r = .77. This is similar to the result from the first experiment, suggesting an information processing rate around 3 bits/s during dragging. The correlation was higher in the latter case, however, yielding

MT = 611 + 383 log2(A / H + 0.5)

(24)

with r = .98. Considering the argument just presented (that the width of the terminating character in a drag operation is a better substitute for target width), the improved correlation is fully expected because character width was positively correlated with character height. Characters with heights of 0.4, 0.5, and 1.2 cm had widths of 0.17, 0.21, and 0.51 cm respectively.

For the point-select tasks, four models were tested in an effort to explore further the nature of target width in Fitts' model when targets are words. The status quo model was tested, as was a model substituting the target height for W. It was also conjectured that the "border of the text object closest to the start" (p. 231) might also be a reasonable substitute for target width; and so, W+H was entered as a candidate model. The area of the target, W×H, was also tested. In order of correlations, the models yielded the following prediction equations for movement time (ms):

Width	Prediction Equation	Correlation
H	MT = 742 + 179 log2(A / H + 0.5)	.93
W+H	MT = 1185 + 128 log2(A / (W + H) + 0.5)	.62
W×H	MT = 1347 + 169 log2(A / (W × H) + 0.5)	.61
Status quo	MT = 1216 + 179 log2(A / W + 0.5)	.46

The results above are consistent with the smaller-of theory in that the model substituting H for W had no conditions in which the target was narrower than it was high (unlike the first experiment for W = 1 character). Surprising, however, is the extremely poor showing of the status quo model. An r as low as .46 is very rare in Fitts' law research. Besides, the conditions used in this experiment were very similar to those in the text selection task used by Card et al. (1978), who obtained r = .91 with the same model.