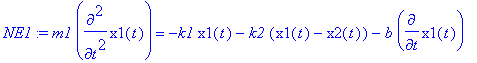
Coupled spring-mass systems

The spring-mass system under gravity (without and with friction) was discussed in the worksheet HOmovie.mws (without and with the application of a driving force). Here we discuss a system with twice the number of degrees of freedom, namely a spring-mass system to which another spring-mass system is connected. We do not include gravity, and are interested in studying the the added features in the solutions. Martha Abell and James Braselton (Differential Equations using MapleV) obtain the solutions to the problem using the Laplace transform (a technique used particularly by engineering students to solve ODes arising in mechanics and electric circuits).

The set-up of the problem is as follows: we assume horizontal motion (gravity is balanced by an air track with a variable amount of friction; we ignore the friction in the springs). We label the masses as m 1, and m 2, the spring constants as k 1 and k 2, the positions as x 1( t ) and x 2( t ), etc.. Spring 1 is attached to a fixed point, mass m 1 to its other end, and spring 2 is attached to m 1, while m 2 is attached to the other end of spring2. We measure x 1( t ) and x 2( t ) from the equilibrium positions of springs 1 and 2 respectively. This implies that mass m 1 experiences a Hooke force from spring 1 in the form - k 1* x 1( t ), and from spring 2 (which is attached at the other end) in the form - k 2*( x 1( t )- x 2( t )). The force for spring 1 is obvious, and the latter is true since: (i) if the equilibrium position for spring 2, x 2( t ) coincides with the equilibrium position of spring 1, i.e., x 1( t ) there is no force, and (ii) if x 2( t ) is larger than x 1( t ) the second spring tends to balance the effect of the first spring, while if it is smaller, it will pull in the same direction as spring 1. Thus, we have for spring 1 (including friction):

> restart; with(plots):

Warning, the name changecoords has been redefined

> m1:='m1': m2:='m2': k1:='k1': k2:='k2': b:='b':

> x1(t):='x1(t)': x2(t):='x2(t)':

> NE1:=m1*diff(x1(t),t$2)=-k1*x1(t)-k2*(x1(t)-x2(t))-b*diff(x1(t),t);

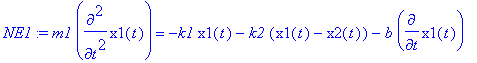
For the second mass we have a simpler force assignment, as it is free at one end; however, the the force from spring 2 acts on it in a way that depends on both positions (similarly, but opposite in sign as in the action on mass m1):

> NE2:=m2*diff(x2(t),t$2)=-k2*(x2(t)-x1(t))-b*diff(x2(t),t);

We assume MKSA (SI) units again, i.e., masses in kg, distances in m, times in s, b in Ns/m, k in N/m, etc.

The initial conditions have to be specified in some way. We pick both positions at equilibrium, and masses m 1 and m 2 moving with the same velocity. A total of 4 quantities have to be specified, as we have two coupled 2nd order ODEs. For a start, we pick the two masses to be equal, and vary the spring constants.

We can ask ourselves whether we can set them, e.g., in such a way that mass m 2 essentially follows mass m 1.

First of all, one has to understand that the location of mass m 2 with respect to the laboratory frame is given by x 1( t )+ x 2( t ).

Before beginning to play seriously with the solutions it helps to figure out some limiting cases:

(i) suppose k 1 is much bigger than k 2, i.e., spring 1 is much stiffer than spring2, and the motion is started with spring 1 out of equilibrium (position or velocity):

in this case equation NE1 corresponds to an harmonic oscillator for x 1 with a small perturbation; it makes sense to find an approximate solution for x 1( t ) without the coupling to x 2( t ); in the equation for mass m 2 we can think of the term involving x 1( t ) as a predetermined driving force. The motion for m 2 in the lab frame will be complicated. It is worthwhile to begin the explorations with this case, and to observe whether the expectations are fulfilled.

(ii) same as in (i), except that spring 2 is started away from equilibrium, while spring 1 starts at rest in the equilibrium position x 1(0)=0:

in this case the motion in x 1 remains small; mass m 2 behaves as a perturbed harmonic oscillator.

(iii) suppose k 2 is much bigger than k 1:

irrespective of whether the initial energy (motion) is in spring 1 or spring 2, the motion corresponds of oscillations around x 1( t )= x 2( t ), the net result being damped near-harmonic oscillations for mass m 2 in the lab frame.

(iv) comparable spring constants: the motion is complicated with an exchange of energy between the springs happening continuously. This is the result of both oscillators being in resonance.

> m1:=1; m2:=1; k1:=4; k2:=5; b:=1/10;

> IC:=x1(0)=0,D(x1)(0)=1/2,x2(0)=0,D(x2)(0)=0;

This initial condition implies that both masses move in unison at t =0, i.e., there is no relative displacement, and no relative velocity between masses m 2 and m 1.

In Maple 5.01 one needs to specify the Laplace method to obtain a solution. In Maple 6.0 a solution is obtained without this hint (and by a different method).

> sol:=dsolve({NE1,NE2,IC},{x1(t),x2(t)},method=laplace);

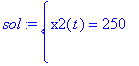
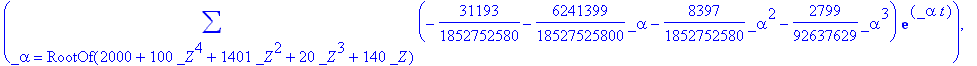
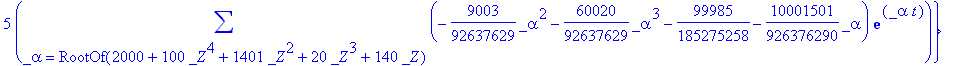
> assign(sol);

Now that the solution is assigned, we can simply type:

> x1(t);

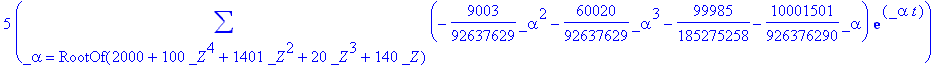
but not:

> x1(1);

> simplify(%);

Therefore, we define mappings based on x1(t) and x2(t). Note that assigning a solution has the drawback, that one has to unassign the dependent variables before re-using it. This was the reason for statements of the type: x1(t):='x1(t)': before defining the Newton equation. It has to be executed before re-using the assignment with a new choice of parameters in the same session.

> X1:=unapply(Re(x1(t)),t): X2:=unapply(Re(x2(t)),t):

> plot([X1(t),X2(t),X1(t)+X2(t)],t=0..40,color=[red,blue,green]);

From the graph of the solutions for both positions we note several things:

(i) mass m 2 indeed follows m 1. The interpretation of x 2( t ) is that the second spring-mass system does carry out oscillations around its equilibrium;

(ii) the solutions imply that we are running a simulation of some kind of superspring: the springs can move to both sides of the equilibrium position (this means that theu are pre-stretched), but more importantly, the two masses can switch positions (they can pass through each other).

(iii) for the motion of mass m 2 in the lab frame we obtain deformed damped harmonic oscillations for many intial conditions.

The next step in understanding the solution is to generate an animation as in HOmovie.mws. We draw the system horizontally to stress that gravity is not involved (apart from providing the friction, which is reduced by the airtrack). For the drawing we will choose the masses to be thin vertical slabs. As before, we pick a width for the springs, as well as their number of turns.

> w:=0.2: nT:=10:

Given a position for the mass y(t) we divide this length into 2 nT segments, and generate a list of points which alternate on the left and right.

> DL:=proc(t) local i,L,d1,d2,le1,le2,t0,x10; global w,nT; t0:=evalf(t);

> d1:=evalf(X1(t0)/(2*nT+1)); le1:=1; le2:=1; L:=[[0.,0.],[d1*0.5,w]]:

> for i from 1 to nT do: L:=[op(L),[d1*(2*i-0.5),-w],[d1*(2*i+0.5),w]]; od: L:=[op(L),[X1(t0),0.],[X1(t0)-w/80,1.1*w],[X1(t0)+w/80,1.1*w],[X1(t0)+w/80,-1.1*w],[X1(t0)-w/80,-1.1*w],[X1(t0),0.]]; d2:=evalf(X2(t0)/(2*nT+1)); x10:=X1(t0); L:=[op(L),[x10+d1*0.5,w]]: for i from 1 to nT do: L:=[op(L),[x10+d2*(2*i-0.5),-w],[x10+d2*(2*i+0.5),w]]; od: L:=[op(L),[x10+X2(t0),0.],[x10+X2(t0)-w/80,1.1*w],[x10+X2(t0)+w/80,1.1*w],[x10+X2(t0)+w/80,-1.1*w],[x10+X2(t0)-w/80,-1.1*w],[x10+X2(t0),0.]]; end:

> PL:=seq(plot(DL(j_t/10)),j_t=1..320):

> display(PL,insequence=true,axes=boxed);

An interesting graph is obtained by plotting parametrically the position of m 2 vs the position of m 1: if we choose both masses to be at equilibrium initially, the plot starts at the origin.

>

> plot([X1(t),X2(t),t=0..10]);

We proceed by performing a simulation of a system that is more easily set up on an air track. Three springs (e.g., of equal spring constant k ) hold two (e.g., equal) masses m 1 and m 2 between themselves. The springs are pre-stretched by this set-up, so that they all can be compressed and stretched by the motion of the masses.

Mass m 1 is attached on one side to spring 1 (characterized by k 1), mass m 2 to spring k 2, and both are connected by spring k 3.

It is best to use a coordinate system that uses the equilibrium positions for springs 1 and 2 as the coordinates and of opposite sign to each other. That way the equaations of motion are cast into symmetrical form. The middle spring's compression is measured by x 1+ x 2.

For this choice of coordinates the force on m 1 consists of - k 1*x1, and - k 3*( x 1+ x 2). Similarly, for m 2 we have - k 2*x2, and - k 3*( x 1+ x 2)

> restart; with(plots):

Warning, the name changecoords has been redefined

> m1:='m1': m2:='m2': k1:='k1': k2:='k2': k3:='k3': b:='b':

> x1(t):='x1(t)': x2(t):='x2(t)':

> NE1:=m1*diff(x1(t),t$2)=-k1*x1(t)-k3*(x1(t)+x2(t))-b*diff(x1(t),t);

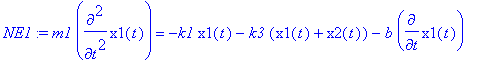
> NE2:=m2*diff(x2(t),t$2)=-k2*x2(t)-k3*(x1(t)+x2(t))-b*diff(x2(t),t);

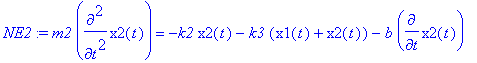
It helps to choose a weak coupling between the two oscillators, i.e., a weak spring between masses m 1 and m 2.:

> m1:=1; m2:=1; k1:=1; k2:=1; k3:=1/10; b:=1/50;

> IC:=x1(0)=0,D(x1)(0)=1,x2(0)=0,D(x2)(0)=0;

> sol:=dsolve({NE1,NE2,IC},{x1(t),x2(t)},method=laplace);

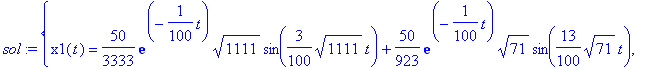
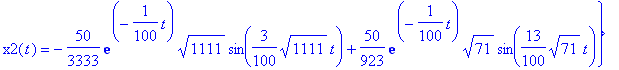
> assign(sol);

> X1:=unapply(Re(x1(t)),t): X2:=unapply(Re(x2(t)),t):

> plot([X1(t),X2(t)],t=0..60,color=[red,blue]);

Interestingly enough, if we look at the difference of the solutions, we find that it satisfies simple, damped harmonic motion (subtract the Newton equations):

> plot(X1(t)-X2(t),t=0..60,color=blue);

We observe the so-called beats phenomenon: the masses oscillate alternatingly. The opposite sign definition of x 1 and x 2 is responsible for the apparent intial movement of mass m 2 in the opposite direction of the oscillation of m 1.

Now we need to re-write our animation program. While it was straightforward to understand the beat phenomenon based on the deviations of masses m 1 and m 2 from the equilibrium positions, our graph of the entire system requires a translation into the laboratory frame.

We omit the outer two springs in the drawing, and choose an arbitrary length (2*Le1) for the initial length of the middle spring.

> w:=0.2: nT:=10:

Given a position for the mass y(t) we divide this length into 2 nT segments, and generate a list of points which alternate on the left and right.

> DL:=proc(t) local i,L,d1,d2,t0,x10,x20,Le1; global w,nT; t0:=evalf(t);

> Le1:=1; d1:=evalf((2*Le1-X1(t0)-X2(t0))/(2*nT+1)); x10:=-Le1+X1(t0); x20:=Le1-X2(t0); L:=[[x10,0.],[x10-w/80,1.1*w],[x10+w/80,1.1*w],[x10+w/80,-1.1*w],[x10-w/80,-1.1*w],[x10-w/80,1.1*w],[x10,0.],[x10+d1*0.5,w]]:

> for i from 1 to nT do: L:=[op(L),[x10+d1*(2*i-0.5),-w],[x10+d1*(2*i+0.5),w]]; od: L:=[op(L),[x20,0.],[x20-w/80,1.1*w],[x20+w/80,1.1*w],[x20+w/80,-1.1*w],[x20-w/80,-1.1*w],[x20,0.]]; end:

> PL:=seq(plot(DL(2*j_t/10)),j_t=0..350):

> display(PL,insequence=true,axes=boxed);

If we extend the number of frames such that at the end the solution almost connects to the intial condition (for small enough friction this is achievable), then the continuous simulation in HTML will look realistic.

One should try initial conditions that correspond to the two fundamental modes:

(i) the masses moving together (no compression of the spring connecting m 1 and m 2);

this can be achieved by picking opposite, equal in magnitude velocities for d x 1/d t and d x 2/d t at t =0 (as x 1 and x 2 have opposite sign).

(ii) the masses moving against each other.

These two modes correspond to motions described by a single Newton equation in the coordinates q 1= x 1+ x 2, and q 2= x 1- x 2 respectively.Verify that the two Newton equations decouple in these two cases, and that the oscillation frequencies are different.

There are mathematical ways to understand the appearance of so-called normal modes, i.e., modes where the motions of m 1 and m 2 reduce to a single degree of freedom. One technique is to write the system of two second-order equations as a system of four coupled first-order equations, and to diagonalize the coefficient matrix. The transformed variables become q 1 and q 2.

Let us see whether the the solution for one of the masses (in the general, coupled case, i.e., for an intial condition where the beat phenomenon occurs) knows about the frequencies associated with the normal modes. A Fourier transform from the time to the frequency domain should reveal this information.

A look at the solution shows indeed that we have a superposition of two solutions with particular frequencies. The symbolic solution was given above. We read out that both frequencies are very close:

> evalf(X1(t));

For the beat phenomenon to be prominent we need, in fact, the closeness of the two frequencies. Instrument tuners (and orchestras) know that two strings are out of tune if the wobbling sound associated with the beat phenomenon is heard. The wobble disappears only if the two frequencies get very close to each other.

Fourier analysis can be performed analytically on simple functions.

> with(inttrans);

> fourier(sin(t),t,f);

> fourier(sin(t)+cos(t/2),t,f);

Note that the cosine components acquire real amplitudes, while the sine components have imaginary amplitudes, and that the frequency spectrum is symmetric.

As we have an initial-value problem, and the damping would result in a blow-up for negative times, we are interested in a transform that integrates over positive times only. Obvious candidates are fourier cosine, and fourier sine transforms. The fourier sine transform gives a very reasonable result.

>

> fouriersin(x1(t),t,f);

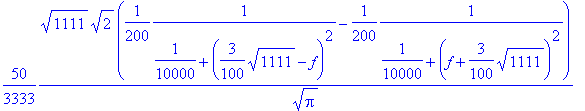
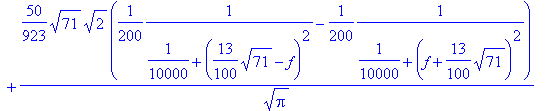
> plot(%^2,f=0.9..1.2);

We find that the frequency spectrum has a finite width about the natural frequencies. We leave it as an exercise to vary the damping constant and to verify that the spectrum approaches that of delta functions at the natural frequencies for the case of weaker damping, and vice versa that it broadens, if the friction constant b is increased.

For the fourier cosine transform we find that the squared amplitude vanishes at the natural frequencies.

> fouriercos(x2(t),t,f);

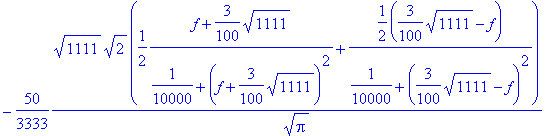
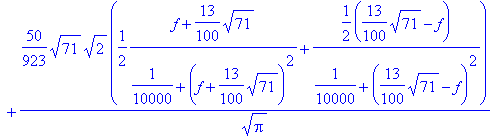
> plot(%^2,f=0.9..1.2);

For more complicated time signals one performs discrete Fourier transforms to unravel the frequency content.

We repeat and strengthen a statement made before about the natural frequencies. One might wonder why two different frequencies appear for the apparently symmetrical system of two identical masses. We have chosen identical springs to attach the masses to their respective sides and a weak spring to couple them together. The student is encouraged to re-run the simulations, and the frequency analysis with a stronger (and weaker) coupling between the two masses. The two different natural modes arose obviously for the symmetrical set-up as those where the masses do not compress the spring which couples them (presumably the lower-energy mode), and the one where in addition to compressing/expanding their support springs the masses compress/expand the coupling spring (the higher-frequency mode). It is for weak coupling that the frequencies become nearly degenerate (almost equal), and the beat phenomenon occurs (which is even more fascinating to watch in real life than on the computer screen; try to put together your own pendula coupled by a very weak rubber band). Which of the two motions has the higher/lower frequency is demonstrated by the decoupling of the equations carried out below.

We complete the calculations by carrying out the transformation of the Newton equations for our choice of parameters.

> x1(t):='x1(t)': x2(t):='x2(t)':

> m1:=1; m2:=1; k1:=1; k2:=1; k3:=1/10; b:=1/50;

> NE1:=m1*diff(x1(t),t$2)=-k1*x1(t)-k3*(x1(t)+x2(t))-b*diff(x1(t),t);

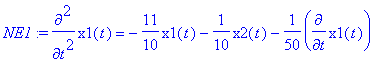
> NE2:=m2*diff(x2(t),t$2)=-k2*x2(t)-k3*(x1(t)+x2(t))-b*diff(x2(t),t);

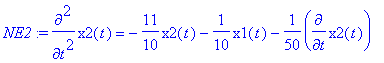
> NE1p:=subs(x1(t)=q1(t)-q2(t),x2(t)=q1(t)+q2(t),NE1);

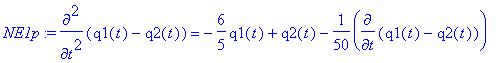
> NE2p:=subs(x1(t)=q1(t)-q2(t),x2(t)=q1(t)+q2(t),NE2);

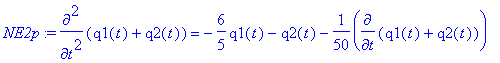
> NE1pp:=NE1p+NE2p;

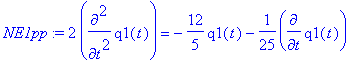
> NE2pp:=NE1p-NE2p;

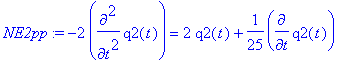
We have decoupled the two differential equations. Let us find the solutions.

> sol1:=dsolve(NE1pp,q1(t));

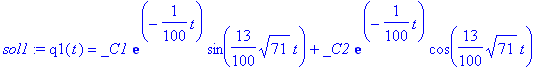
> evalf(rhs(sol1));

> sol2:=dsolve(NE2pp,q2(t));

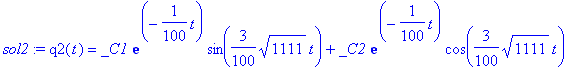
> evalf(rhs(sol2));

Now, the lower frequency occurs in the mode described by q 2( t ) = 2( x 2( t ) - x 1( t )). This mode is the one where the masses run in parallel (remember that according to our convention x 1 and x 2 have opposite sign, and that x 1/ x 2 measures the displacement of the respective mass from the equlibrium point of the spring which connects it to its respective support).

For the case of arbitrary masses and spring constants one would have to find the right linear combinations to perform the decoupling. It is for this case that one prefers the mathematical machinery of decoupling systems of first-order differential equations with constant coefficients by means of a similarity transformation (diagonalization of the matrix of coefficients).

>