Ehrenfest's theorems

We first develop a procedure which propagates a one-dimensional wavepacket in space and time. Then we demonstrate the validity of the theorems, which determine the time evolution of position and momentum expectation values. This allows one to investigate the semi-classical limit in which the position and momentum average values satisfy Hamilton's equations of motion.

The first step involves setting up a coordinate- and momentum-space discretization.

> restart;

> dx:=0.3; n:=10; N:=2^n;

> dp:=evalhf(2*Pi/(N*dx));

> readlib(FFT):

> with(LinearAlgebra): Digits:=15:

> xv:=Vector(N): yR:=Vector(N): yI:=Vector(N): pv:=Vector(N):

> for i from 1 to N do:
xv[i]:=evalhf((i-N/2-1/2)*dx); if i < N/2+1 then
pv[i]:=evalhf((i-1)*dp); pv[N-i+1]:=evalhf(-i*dp); fi; od:

> p_max:=(N/2-1)*dp;

The maximum available momentum value on the mesh puts a limit on the momentum distribution that we can choose for the intial wavepacket! It can be increased by reducing dx.

Now we set up the initial wavepacket: we can choose the initial average position, average momentum, and momentum spread. We should also have a choice for the shape of the wavepacket. To make matters simple we choose a Gaussian shape:

> x0:=-50; p0:=1; sigma:=1/4;

> fx:=exp(-sigma^2*(x-x0)^2/2)*exp(I*p0*x)/(Pi/(sigma)^2)^(1/4);

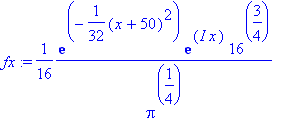
> int(evalc(conjugate(fx)*fx),x=-infinity..infinity);

The initial wavepacket is normalized properly! The width parameter sigma describes the momentum spread around the average value.

We can calculate the average momentum:

> int(evalc(conjugate(fx)*(-I)*diff(fx,x)),x=-infinity..infinity);

The average position:

> int(evalc(conjugate(fx)*x*fx),x=-infinity..infinity);

We can also calculate the deviation from the average position:

> sqrt(int(evalc(conjugate(fx)*(x-x0)^2*fx),x=-infinity..infinity));

> plot([Re(fx),Im(fx)],x=-75..15,color=[red,blue]);

Exercise 1:

Vary the parameters that determine the Gaussian wavepacket (particularly the momentum spread), and observe the change in the packets appearance (in particular, its spread in position).

> for i from 1 to N do: yR[i]:=evalf(subs(x=xv[i],Re(fx))); yI[i]:=evalf(subs(x=xv[i],Im(fx))); od:

Now we pick a potential function. In principle, the potential should not vary as a function of x in the region where the wavepacket is defined initially, i.e., that region should be potential-free.

> x0;

> Vp:=x->2*(exp((x-100)/50)-exp((x0-100)/50));

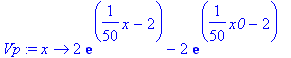
> Vi:=Vector(N):
for i from 1 to N do: Vi[i]:=evalf(Vp(xv[i])); od:

> with(plots):

Warning, the name changecoords has been redefined

We graph the real and imaginary parts of the wavepacket's discretized wavefunction displaced by the amount of average initial kinetic energy along with the potential. The baseline for the wavefunction plot indicates the classical turning point (where it intersects the potential energy graph). Note that the variation in the potential energy is gentle at first (approximately constant force over the extent of the wavepacket), while the variation becomes more steep as one approaches the turning point.

> P1:=plot([seq([xv[i],Vi[i]],i=1..N)],color=green):

> P2:=plot([seq([xv[i],p0^2/2+yR[i]],i=1..N)],color=blue):

> P3:=plot([seq([xv[i],p0^2/2+yI[i]],i=1..N)],color=red):

> display([P1,P2,P3],view=[-100..100,-0.5..1.5]);

> dt:=0.1: dth:=0.5*dt:
t:=0;

> T2:=Vector(N): V1:=Vector(N):

> for i from 1 to N do: T2[i]:=exp(-I*0.5*pv[i]^2*dth); od:

> for i from 1 to N do: V1[i]:=exp(-I*Vi[i]*dt); od:

> Tstep:=proc() local i,s; global y,xv,pv,Vi,Eni,n,N,yR,yI,T2,V1,t,dt,dx;
evalhf(FFT(n,var(yR),var(yI)));
for i from 1 to N do: y:=T2[i]*(yR[i]+I*yI[i]); yR[i]:=Re(y); yI[i]:=Im(y); od:
evalhf(iFFT(n,var(yR),var(yI)));
for i from 1 to N do: y:=V1[i]*(yR[i]+I*yI[i]); yR[i]:=Re(y); yI[i]:=Im(y); od:
evalhf(FFT(n,var(yR),var(yI)));
for i from 1 to N do: y:=T2[i]*(yR[i]+I*yI[i]); yR[i]:=Re(y); yI[i]:=Im(y); od:
evalhf(iFFT(n,var(yR),var(yI))); t:=(t+dt);
t; end:

> Fx:=unapply(-diff(Vp(x),x),x);

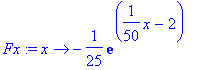
At time t = 0 we compare the force evaluated at the average position to the force expectation value:

> F0:=evalf(Fx(x0));

> Fexp:=dx*add((yR[i]^2+yI[i]^2)*Fx(xv[i]),i=1..N);

We set up a time loop with an exterior loop in which we store graphs of the time evolution of the wavefunction and the momentum-space probability at a large time interval. An inner loop steps over dt: in this loop we collect information about the position and force operator expectation values. Our aim is to analyze these expectation values to verify Ehrenfest's theorem, as well as to compare with classical time evolution for the average position.

The time loop requires a large amount of CPU time. Be prepared for hours to complete the calculation!

> Nt:=55: EKL:=[]: EPL:=[]:

> xL:=[[t,x0]]: FxL:=[[t,Fexp]]:

> for jt from 1 to Nt do:

> for it from 1 to 50 do:

> t_i:=Tstep();

> x0t:=dx*add((yR[i]^2+yI[i]^2)*xv[i],i=1..N): xL:=[op(xL),[t_i,x0t]]: Fexp:=dx*add((yR[i]^2+yI[i]^2)*Fx(xv[i]),i=1..N): FxL:=[op(FxL),[t_i,Fexp]]:

> od:

> Pre[jt]:=plot([seq([xv[i],p0^2/2+yR[i]],i=1..N)],color=blue):

> yRt:=Vector(N): yIt:=Vector(N): for i from 1 to N do: yRt[i]:=yR[i]: yIt[i]:=yI[i]: od: evalhf(FFT(n,var(yRt),var(yIt)));
EP:=dx*add(Vi[i]*(yR[i]^2+yI[i]^2),i=1..N); EPL:=[op(EPL),[t_i,EP]]: EK:=add(pv[i]^2/2*(yRt[i]^2+yIt[i]^2),i=1..N)/add(yRt[i]^2+yIt[i]^2,i=1..N); EKL:=[op(EKL),[t_i,EK]]: Pmom[jt]:=plot([seq([pv[i],yRt[i]^2+yIt[i]^2],i=1..N)],color=black,style=point):

> od:

> B:=animate(Vp(x),x=-100..120,d=-1..1,frames=Nt,color=green):

> A:=display([seq(Pre[j],j=1..Nt)],insequence=true,view=[-100..120,-0.1..0.9]):

> display(A,B,thickness=3);

The wavepackets momentum distribution evolves as a function of time: the potential slows down the wavepacket, forces a turn-around, and then accelerates it to the left. The momentum distribution changes as a result of the interaction: it becomes quite narrow as the wavepacket approaches the turning point, and then broadens again after the turnaround.

> display([seq(Pmom[j],j=1..Nt)],insequence=true,view=[-2..2,0..500],symbol=diamond);

Let us check the time evolution of the energy expectation values: kinetic, potential, and total energy are displayed:

According to the equations of motion for observables in QM the expectation value of the total energy has to remain constant, as [H,H]=0 and H does not depend on timein our problem. The constancy of the energy expectation value serves to demonstrate that the numerical propagation of the wavepacket is accurate.

We can also see how kinetic energy on average is converted into potential energy and back as the wavepacket scatters from the potential wall.

> ETL:=[seq([EKL[i][1],EKL[i][2]+EPL[i][2]],i=1..Nt)]:

> plot([EKL,EPL,ETL],color=[red,blue,green],thickness=3);

How small is the kinetic energy at the turning point?

> EKL[27],EKL[28],EKL[29];

We did not resolve the time axis well enough to answer the question whether the average kinetic energy actually becomes zero! A detailed graph of the neighborhood of t = 135-140 suggests that it does not; this makes sense as the wavepacket cannot be a function with zero curvature. Nevertheless, it does come quite close to this limit.

Now we compare the evolution of the position expectation value with purely classical evolution. In classical evolution the force is evaluated only at the position x0(t) to control the further time evolution. The quantum calculation of the average position via Ehrenfest's theorem would rely on a sampling of the force over the extent of the wavepacket. At early times we expect the two methods to agree, at later times when the wavepacket spreads and hits a region where the potential varies more rapidly we can expect differences.

> X1:=plot([xL],color=red):

> NE:=diff(x(s),s$2)=Fx(x(s));

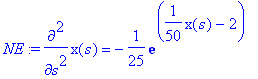
> IC:=x(0)=x0,D(x)(0)=p0;

> sol:=dsolve({NE,IC},x(s),numeric,output=listprocedure);

> x_c:=subs(sol,x(s));

> x_c(10);

> X2:=plot('x_c(s)',s=0..Nt*dt*50,color=blue):

> display(X1,X2,thickness=3);

Note how the classical calculation for the position expectation value predicts the turnaround at a slightly later time, and a larger value of x0 at which the turnaround occurs.

To verify that Ehrenfest's theorem holds for the numerical calculation we can check whether the second derivative of x0(t) agrees with the expectation value of the force.

> x2pL:=[]: for i from 2 to nops(xL)-1 do: x2pL:=[op(x2pL),[xL[i][1],(xL[i+1][2]+xL[i-1][2]-2*xL[i][2])/dt^2]]; od:

> A:=plot([seq(FxL[20*i-10],i=1..nops(FxL)/20)],color=red,style=point,symbol=diamond): B:=plot([seq(x2pL[20*i-1],i=1..nops(x2pL)/20)],color=blue,style=point,symbol=cross): display(A,B);

Quite clearly the numerical solution of the TDSE satisfies Ehrenfest's theorem: otherwise the evaluation of the second derivative of the average position with respect to time would not coincide with the expectation value of the force. We can use this as a confirmation of the validity of the numerically obtained result for the position expectation value.

On the other hand, we find that the position expectation value x0(t) follows the classical evolution only to the point where the wavepacket experiences a substantially different amount of acceleration in the front versus back parts. This occurs shortly before the turnaround point.

An interesting question arises: suppose we have a classical statistical ensemble. This ensemble contains faster and slower particles. What is the evolution of the particle density? The faster particles will have more energy, i.e., a turning point further to the right, than the slower particles.

Classical statistical ensemble simulation

We dial up an initial distribution that corresponds to a wavepacket: intially there is no correlation between the particle position and momentum.

> NEns:=50:

> x0,p0,sigma;

We need a Gaussian distribution in position (width 1/sigma) around x0, and a distribution in momentum around p0. This can be achieved with the normal distribution.

> Pval:=Vector(NEns): Xval:=Vector(NEns):

> with(stats):

> xrand:=stats[random, normald](NEns):

> for i from 1 to NEns do: Pval[i]:=p0+sigma*xrand[i]: od:

> xrand:=stats[random, normald](NEns):

> for i from 1 to NEns do: Xval[i]:=x0+(1/sigma)*xrand[i]: od:

The expectation value follows from the ensemble average:

> xC0:=add(Xval[i],i=1..NEns)/NEns;

> pC0:=add(Pval[i],i=1..NEns)/NEns;

> EPC0:=evalf(add(Vp(Xval[i]),i=1..NEns)/NEns);

> EKC0:=add(0.5*Pval[i]^2,i=1..NEns)/NEns;

For each testparticle (ensemble member) we would like to propagate the Newton equation. We can calculate expectation values as in quantum mechanics, except that they are calculated as ensemble averages.

We have a time loop as before, and a particle loop inside.

> t_i:=0:

> EKCL:=[[t_i,EKC0]]: EPCL:=[[t_i,EPC0]]:

> xCL:=[[t_i,xC0]]: for jt from 1 to Nt do: t_f:=evalf(t_i+50*dt): for j from 1 to NEns do:

> IC:=x(t_i)=Xval[j],D(x)(t_i)=Pval[j];

> sol:=dsolve({NE,IC},x(s),numeric,output=listprocedure);

> x_c:=subs(sol,x(s)); p_c:=subs(sol,diff(x(s),s));

> Xval[j]:=x_c(t_f): Pval[j]:=p_c(t_f): od: t_i:=t_f:

> xC:=add(Xval[i],i=1..NEns)/NEns;

> EPC:=evalf(add(Vp(Xval[i]),i=1..NEns)/NEns); EKC:=add(0.5*Pval[i]^2,i=1..NEns)/NEns;

> EKCL:=[op(EKCL),[t_i,EKC]]: EPCL:=[op(EPCL),[t_i,EPC]]: xCL:=[op(xCL),[t_i,xC]]:

> od:

> ETCL:=[seq([EKCL[i][1],EKCL[i][2]+EPCL[i][2]],i=1..Nt)]:

> plot([EKCL,EPCL,ETCL],color=[red,blue,green],thickness=3);

The fact that the kinetic energy does not vanish at the turning point for the average position means that the particles do not all reach their respective turning points at the same time.

> X3:=plot(xCL,color=green):

> display(X1,X2,X3,thickness=3);

The classical statistical mechanics simulation has a substantially lower value for the location of the turning point: we can conclude that the wavepacket's tunneling behaviour allows it to penetrate the potential wall (which was very evident from watching the real part of the wavefunction). It is interesting that the classical calculation for the expectation value, which initially coincides with the QM calculation for the wavepacket's true expectation value (justified by Ehrenfest's theorem) leads to a slightly larger excursion into the classically forbidden regime, and to a delay in the return of the wavepacket. This suggests that the tunneling process (as calculated by the numerical solution of the TDSE) may involve shorter time scales than classical propagation. The question of tunneling time, and its experimental verification in particular, represents an active area of research currently.

>