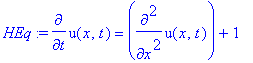HeatEqn.html

HeatEqn.html HeatEqn.mws

Heat Equation

A derivation is given in the notes (jpg-files in the folder). We follow David Betounes: Partial Differential Equations for Computational Science, Springer Verlag 1997, ISBN 0-387-98300-7.

We begin with a one-dimensional example.(Example 2.2 in the book). A thin rod lies on the x-axis from 0 to 1 (appropriate units are chosen to make the equation dimensionless).

At time zero the rod is at zero temperature (inital condition). u(x,0) = 0 .

On the left boundary the rod is kept at zero temperature by a heat bath (make it zero Celsius to avoid trouble with physics, zero Kelvin are not reachable!).

u(0,t) = 0 for t > 0

On the right boundary the rod is insulated, i.e., no flow of heat across this boundary is permitted. diff(u(x,t),x)[@x=1,t>0] = 0 (this is not Maple syntax!)

The heat equation contains a source term, i.e., it is not homogeneous. The inhomogeneity is chosen as a constant, i.e., heat is being generated in all locations of the rod 0 < x < 1 (not at x = 0 ).

The heat equation has a steady-state solution, i.e., a solution that is being reached for large t . For this to be possible, a solution u(x,t) has to be found with vanishing time derivative in the limit of large time. This function will depend on the position variable x only.

> restart;

> HEq:=diff(u(x,t),t) = diff(u(x,t),x$2) + 1;

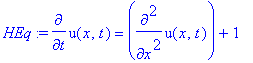In order to express the boundary condition at x=1 we have to understand how the D operator works on functions of several variables:

> BC:=u(0,t)=0,D[1](u)(1,t)=0;

> IC:=u(x,0)=0;

> sol:=pdsolve({HEq,BC,IC},u(x,t));

$sol := {u(x,t) = _C1*_C3*exp(_c[1]*t)*exp(_c[1]^(1/2)*x)+_C3*exp(_c[1]*t)*_C2/exp(_c[1]^(1/2)*x)-1/2*x^2-1/_C1*_C2*x-1/_C1*_C3}$

It seems as if Maple has not found a unique solution. Four constants appear in the answer. Is it possible that many solutions truly exist?

Let us extract the steady state solution by solving the ordinary differential equation that follows from setting the time derivative to zero.

Let us call the steady-state solution w(x) :

> DE:=diff(w(x),x$2)+1=0;

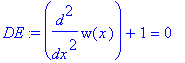> BCode:=w(0)=0,D(w)(1)=0;

> solDE:=dsolve({DE,BCode});

> plot(rhs(solDE),x=0..1);

The heat equation is supposed to describe the evolution from u(x,0)=0 towards u(x,infinity)=w(x) .

Note how the boundary conditions are satisified (prescribed temperature value on the left, and zero derivative on the right). These conditions have to be satisfied at all times.

The equation is usually solved by the separation of variables method. Before we do that let us look at the solution generated by maple. Without the boundary conditions the following answer is obtained:

> sol:=pdsolve(HEq);

$sol := `&where`(u(x,t) = _F1(x)*_F2(t)-(1/2*_C1*x^2+_C2*x+_C3)/_C1,[{diff(_F2(t),t) = _c[1]*_F2(t), diff(_F1(x),`$`(x,2)) = _c[1]*_F1(x)}])$

Now it becomes clearer what the constants mean: pdsolve is telling us that:

1) there is a time-independent, additive part to the solution, which is characterized by three constants. From our asymptotic solution it is clear that

> solHEq:=subs(_C1=1,_C2=1,_C3=0,rhs(op(1,sol)));

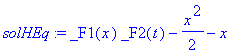The heat equation admits a solution of the form where the transient part is expressed as a product of one-dimensional functions F1(x)*F2(t) . The two functions satisfy simple ordinary differential equations listed in sol .

> eq1:=diff(F2(t),t)=c1*F2(t);

> eq2:=diff(F1(x),x$2)=c1*F1(x);

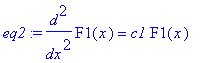> sol_x:=dsolve({eq2,F1(0)=0,D(F1)(1)=0},F1(x));

We are not interested in the trivial solution, so what do we do now?

> sol_x:=dsolve({eq2,F1(0)=0},F1(x));

Somehow we will have to find acceptable solutions (derivative to vanish on the right-hand boundary) by choosing c1 rather than _C2.

> sol_x1:=subs(_C2=1,rhs(sol_x));

> plot(subs(x=1,diff(sol_x1,x)),c1=0..50);

This shows that positive values of c1 won't do the trick. So we try negative values, which makes the solution complex-valued.

> [Re(subs(x=1,c1=-5,diff(sol_x1,x))),Im(subs(x=1,c1=-5,diff(sol_x1,x)))];

> plot([Re(subs(x=1,diff(sol_x1,x))),Im(subs(x=1,diff(sol_x1,x)))],c1=-220..0,color=[red,blue],axes=boxed,numpoints=500);

What are we learning here? We took the condition for the right-hand boundary, and we showed that it can be satisfied by the solution to the spatial ODE provided the separation constant c1 is chosen to be negative. The real part of the condition is always zero (boring, but important). The derivative of the solution at x=1 does vanish when the imaginary part of the expression crosses zero. We can use the integration constant _C2 to make the solution real-valued (by making it imaginary).

Therefore, the product part of the solution, i.e., the transient part, is not unique. There are different choices of c1 that work, and we have to take them all into account in order to find a unique solution that matches our boundary conditions and the initial condition.

Each spatial solution (function F1(x) that satisfies the ODE and the boundary conditions) has an appropriate time solution F2(t) that goes with it. Before we find it, let us look at the spatial modes. First we determine a few of the lowest c1 values accurately.

> sol_c1:='sol_c1': sol_c1[1]:=fsolve(Im(subs(x=1,diff(sol_x1,x))),c1=-10..-0.0001);

> sol_c1[2]:=fsolve(Im(subs(x=1,diff(sol_x1,x))),c1=-50..-10);

> sol_c1[3]:=fsolve(Im(subs(x=1,diff(sol_x1,x))),c1=-100..-50);

> sol_c1[4]:=fsolve(Im(subs(x=1,diff(sol_x1,x))),c1=-150..-100);

> sol_c1[5]:=fsolve(Im(subs(x=1,diff(sol_x1,x))),c1=-250..-150);

Of course, there are infinitely many solutions, and it is not unreasonable to ask at this point whether we will get anywhere at all... Nevertheless, we'll proceed by looking at some of the spatial modes:

> plot([seq(subs(c1=sol_c1[i],I*sol_x1),i=1..5)],x=0..1,color=[red,blue,green,black,brown]);

These functions look familiar. So let us understand why that is so.

The differential equation for the spatial modes is asking: which functions are proportional to their second derivative. This selects the class of exponentials, including complex exponentials. Then we asked the functions to vanish at x=0 , and we wanted real-valued functions. This selected from sines and cosines just sine functions. Next we asked only for those functions which had zero derivative at x=1 . This selected from all sin(sqrt(c1)*x) those with an appropriate wavenumber, i.e., value of c1 . Of those we plotted the lowest four. Functions which do not have too much variation with x should be representable with a few low-lying modes to a reasonable degree of accuracy. This is where our hope comes from: we proceed even though we know that in principle there are infinitely many product solutions.

Let us now understand how the modes evolve in time.

> sol_t:=dsolve({eq1},F2(t));

$sol_t := {F2(t) = _C1*exp(c1*t)}$

We observe that we want negative values of c1 , because this generates dying solutions. Each of the spatial modes dies with time with a time constant of its own! The higher modes (many oscillations) die faster than the lower modes.

Now one might ask, why do we need to worry about dying modes, when the solution to the heat equation starts from u(x,0)=0 ? The answer is that we have the additive asymptotic piece. To be consistent with it, and with the stated initial condition we have to superimpose the modes in such a way that they cancel the asymptotic piece. This we do by a projection method (formally we construct a Fourier series).

> solDE;

> basis:=seq(evalc(subs(c1=sol_c1[i],I*sol_x1)),i=1..5);

We claim that the inner product (dot product) of two basis functions is just the integral of the product of functions from 0 to 1.

> int(basis[1]*basis[2],x=0..1);

> int(basis[1]*basis[3],x=0..1);

To numerical accuracy the functions are orthogonal! What about the normalization?

> int(basis[1]*basis[1],x=0..1);

> int(basis[2]*basis[2],x=0..1);

OK, so the functions are normalized in a funny way, but that shouldn't deter us. Verify the orthogonality and normalization for some of the other basis functions (or basis vectors in the Hilbert space). Let us expand by calculating projections. To make up for the wrong normalization we re-define the basis functions by dividing by the square root of 2.

> b[1]:=int(rhs(solDE)*basis[1]/sqrt(2),x=0..1);

> b[2]:=int(rhs(solDE)*basis[2]/sqrt(2),x=0..1);

> b[3]:=int(rhs(solDE)*basis[3]/sqrt(2),x=0..1);

> b[4]:=int(rhs(solDE)*basis[4]/sqrt(2),x=0..1);

> b[5]:=int(rhs(solDE)*basis[5]/sqrt(2),x=0..1);

Good news: the projection of the function to be expanded onto higher basis states are getting smaller. We are ready to compare the expansion with the original function:

> FE:=add(b[i]*basis[i]/sqrt(2),i=1..5);

> plot([FE,rhs(solDE)],x=0..1,color=[red,blue]);

We see that the expansion is better than 1% accurate (otherwise we would notice a difference in the graph). Repeat the graph with less than five basis states and observe how the convergence comes about!

Now we are ready to put everything together. The total solution is obtained by multiplying the basis functions with the appropriate time-factors, and by adding the transient and steady-state parts together as required:

> sol_t;

${F2(t) = _C1*exp(c1*t)}$

> FEt:=rhs(solDE)-add(b[i]*basis[i]/sqrt(2)*exp(sol_c1[i]*t),i=1..5);

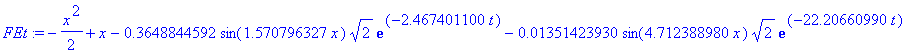> plot([seq(subs(t=j*0.25,FEt),j=1..5)],x=0..1,color=[red,blue,green,black,brown]);

We observe how the solution rapidly approaches the steady state. Explore the time behavior in detail (by choosing different time intervals and more steps j ).

Repeat the observation for a more approximate solution by selecting a smaller expansion in the Fourier series, i.e., in FEt .

Here is a graph in three dimensions. It shows, how well the Fourier expansion approximates the initial condition, and how quickly the asymptotic values are attained.

> plot3d(FEt,x=0..1,t=0..2,axes=boxed);

Rotate the graph to look at the solution from different perspectives.

To remind ourselves that we do not have an exact solution we show the deviation from the intial condition:

> plot(subs(t=0,FEt),x=0..1);

Exercise:

Increase the expansion to 10 basis functions and observe how well the initial condition can be matched.

>