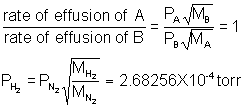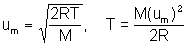
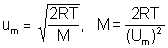
- the estimated um is about 870 ms-1
- using all SI units leads to M = 2.792 X 10-2 kg mol-1 or 27.92 g mol-1
- estimate of um limits answer to 2 sig. figs (i.e. 28 g mol-1)
- if this is a diatomic molecule then each atom has an atomic mass of 14 g mol-1 and therefore the gas must be nitrogen, N2
2) m = M/NA = (2 X 14.0067)/(6.02214 X 1023) = 4.65174 X 10-23 g or 4.65174 X 10-26 kg
3) - estimate um on the T1 curve (use a ruler); um is approximately 400 ms-1
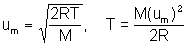
- using all SI units gives T = 270 K (or about 0C)
4) - similar to question 1... estimate um on the T3 curve (roughly 1500 ms-1) and then solve for M
- using all SI units gives M = 1.66 X 10-2 kg mol-1 or 16.6 g mol-1
- hydrocarbons contain only hydrogen and carbon
- a M less than 24 indicates this molecule can only contain one carbon atom
- it must be CH4
5) PV = nRT = NkT
- very important to watch that units are consistent throughout these calculations
a)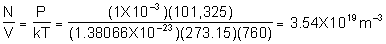 
b)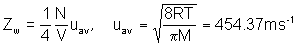 
- use the number density from part a) to get Zw = 4.02 X 1021 m-2s-1
c) 
- use average speed from part b) and number density from part a) to get ZA = 8.74 X 103 s-1
d)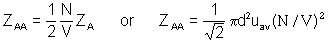 
- simplest method is to use answers from parts a) and c) to get ZAA = 1.55 X 1023 m-3s-1 (other formula will give the same answer)
e)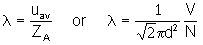 
- simplest method is to use average speed from part b) and answer
from part c) to get 
= 5.20 X 10-2m (other
formula will also give the answer)
6) use the second formula for mean free path in question 5e) and substitute PV = NkT yields
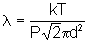
- the mean free path is directly proportional to T and indirectly proportional to P, thus
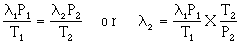
- solve for the mean free path under the latter conditions gives an answer of 7.46 X 10-8 m
7) The collision frequency, Z, is given by Z = ZW X A
where A is the surface area of the inside of the bulb. The surface area
of a sphere is given by A = 4
r2 so we need to be able to calculate r, the
radius of the bulb. The volume of the bulb is exactly 1 L so we can use
to find r = 6.20350 X 10-2m. Substitution back into the original equation, including ZW from 5b), yields a collision frequency of 1.94 X 1020 s-1.
8) rate of effusion = ZW X A, where A is the area of the
orifice given by A = r2 (remember to divide the diameter that was
provided in the question by 2 to get the radius)
- substitution of ZW from part 5b) and the area of the orifice gives
rate of effusion = 1.97119 x 1012 s-1 = (# of molecules)/(time)
- we need to know what 1% of the molecules is
1% of molecules = 0.01 X total number of molecules = 0.01 X number density X volume
- we calculated the number density in part 5a), the volume was given as exactly 1 L, so 1% of the molecules is 3.53519 X 1014
- the time required for 1% of the molecules to effuse can now be calculated by rearranging the formula used above to calculate the rate of effusion
time = (# of molecules)/(rate of effusion)
therefore, for 1% of the molecules to effuse, time = 1.8 X 102 s
9) It follows from Graham's Law that
