1.5 A Rigorous Formulation of Agents' Decision
Having explained the relation between indifference curves and utility functions and the meaning of a unity function we are now in a position to pose the problem solved by the agents. Assume that the price of good 1 is 
and that of good 2 is 
and that the agent has a budget of 
and a utility function 
. The reader may have already guessed that the agent needs to solve a maximization problem which is formulated as below:
s.t. 
Since 
is a monotone increasing function, the inequality 
can be replaced with an equality 
. Thus, one way of solving this problem is by substituting 
in terms of 
and solving an optimization problem with only the non-negativity constraints 
.
We will, however, utilize this opportunity to review the optimality conditions as they play a central role in the portfolio choice problem. Furthermore, we will explain or provide a heuristic proof for the optimality conditions. This proof highlights a relation (duality) between two systems of inequalities that is used later in the Arbitrage Pricing Theory (APT).
In order to state the optimality conditions in a generic way we should decide about a canonical form of an optimization problem. We will define a canonical form as a minimization problem with constraints of the type 
. That is, a problem of the form
s.t. 
, 
Where 
is a vector in 
and 
and 
, 
are functions from 
to 
and 
, 
.
It is easy to see that there is no loss of generality assuming such a canonical form of an optimization problem. The solution of a maximization problem is the same for a minimization problem in which the negative of the objective function 
is minimized. Inequality constraints could be reversed by multiplying the inequality by 
and an equality can be written as a pair of two inequalities. After we develop the optimality condition for the above problem we will apply it to our maximization of utility problem.
Let us first start with the intuition behind the optimality conditions. If 
is a minimum point of 
, subject to the constraint stipulated above, it must be that there is no feasible direction 
“along which one can move away” from 
and reach a point where the value of 
is smaller than the value of 
at 
. Being a feasible point, 
satisfies the constraint, that is 
, 
. The direction 
is feasible if there exists an 
", mathvariant = "normal", fence = "false", separator = "false", stretchy..." align="center" border="0"> such that 
, 
. Moving away from 
along the direction 
, will lead to a point 
for some positive 
.
on 
such that
, for a given 
and 
in 
.
thus equals 
, and if 
is negative it means that moving along the direction 
, 
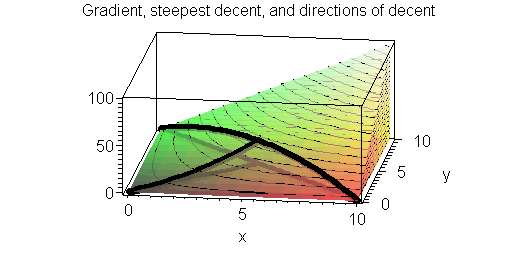
decreases. Footnote 6 A visualization of direction of decent relative to the gradient and the value of the function along these directions is offered below for the utility function of the former section. The graph below demonstrates the direction 
for 
at a point (5,5).
The directions of the negative of the gradient is drawn as a black line in the 
axis that points to the origion, with two other directions that are perpendicular to it. All the direction between the two prepndcualr directions are directions of decent. The movement along these directions is also drawn on the graph of the function so one can realize that these are indeed directions of decent.
| > | NGFradNfun:=plot3d([[5-x,5-x,(5-x)*(5-x)],[5-x,5-x,0],[5-x,5+x,(5-x)*(5+x)],[5+x,5-x,(5+x)*(5-x)],[5-x,5+x,0],[5+x,5-x,0]],x=0..5,y=0..5,axes=box,thickness=4): |
| > |
| > | Util:=plot3d(x*y,x=0..10,y=0..10,axes=box,style=patchcontour,contours = 20,filled=true,orientation=[-82,56],title="Gradient, steepest decent, and directions of decent ",transparency=.2): |
| > |
| > | plots[display](Util,NGFradNfun); |
 |
| > |
| > |
Similarly if 
is a point on the boundary of the feasible set, i.e., it satisfies one of the constraints say 
as equality rather than inequality, and if the function 
is such that 
is not a feasible direction. This is because as we move along 
, 
increases and since at 
, 
there exists an 
", mathvariant = "normal", fence = "false", separator = "false", stretchy = "false", symmetric =..." align="center" border="0">such that 
violates the constraint since 
for every ε in 
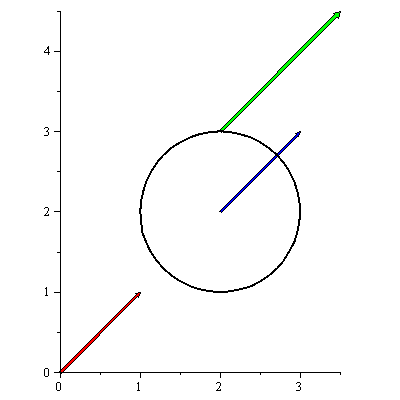
This is illustrated below where the vector 
is the red line. Moving along 
with 
.5 from the point (2,3) is demonstrated by the green line which leads to the point 
. Moving along 
from the point (2,2) with 
is demonstrated by the blue line which ends at 
. The feasible set is demonstrated by the black circle and one can visualize that the direction 
from the point (2,2) is a feasible direction as it is possible to move along it and still stay within the feasible set. On the other hand the direction 
is not a feasible direction from the point (2,3) since moving along it, even with a very small positive
, will result in a point outside the feasible set. The feasible set in this illustration is given by the function
.
| > | V11:=plots[arrow]([<1,1>], width=[0.02, relative], head_length=[0.04, relative], color=red): |
| > | V1122:=plots[arrow](<2,2>,<1,1>, width=[0.02, relative], head_length=[0.04, relative], color=blue): |
| > | V1123:=plots[arrow](<2,3>,<1.5,1.5>, width=[0.02, relative], head_length=[0.04, relative], color=green): |
| > | FeasC:=plot([[2+cos(t),2+sin(t), t=0..2*Pi]], color=[black],thickness=2,scaling=constrained): |
| > | plots[display](V11,V1122,V1123,FeasC); |
 |
| > |
| > |
The derivative of
with respect to 
is given by 
where ▽ denotes the gradient of 
(the vector of partial derivatives) and 
denotes the transpose of 
(a row vector). At the point 
, 
is positive if 
At the point (2,3) we can calculate 
as below
| > | Student:-MultivariateCalculus:-Gradient((x-2)^2+(y-2)^2,[x,y]=[2,3]); |
 |
| > |
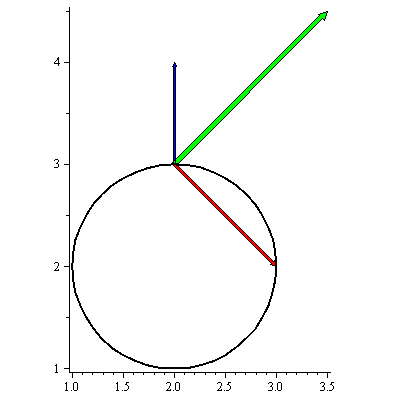
In the graph below the gradient of 
at the point (2,3) is illustrated by the blue line, the direction 
from the point 
by the green line, and the direction 
from the point 
by the red line.
| > | V0123:=plots[arrow](<2,3>,<0,1>, width=[0.02, relative], head_length=[0.04, relative], color=blue): |
| > | V1Neg123:=plots[arrow](<2,3>,<1,-1>, width=[0.02, relative], head_length=[0.04, relative], color=red): |
| > | plots[display](V1123,V0123,V1Neg123,FeasC); |
 |
| > |
You may recall that if 
than the angle between the vector 
and 
is acute, while if the angle between the vector 
and 
is obtuse 
. In the case illustrated above by the green line 
since 
and hence the angle between the vector 
and 
is acute and the green line is not a feasible direction. 
On the other hand the direction 
is a feasible direction from the point 
. It is represented by the red line which points inside the circle. On the circle the value of 
is 1 and inside the circle it is less than 1. Hence moving along this direction does not violate the constraint that requires that 
Feasible directions are therefore those that generate an obtuse angle with the gradients of the binding constraints. A feasible direction 
at a point 
, is characterized by the fact that for each binding constraint 
at 
, i.e., for each 
for which 
, the product of 
and the gradient of 
is negative, that is 
If the point is a minimum point, it must be that there exists no feasible direction along which the objective function decreases. Footnote 7 Since if one existed there would be a feasible point say 
=
for some γ>0 such that 
, but that means that 
could not be the minimum point. Thus, if 
is a minimum point it must be that
for every 
such that 
then 
,
i.e., the function 
increases along each feasible direction 
from 
.
This condition can also be stated as:
Every 
such that 
for 
such that 
, must satisfy 
.
Put into words, every feasible direction from point 
, must be a direction along which 
does not decrease. This condition can also be geometrically visualized.
Assume that there are two binding constraints at a point 
, hence we have vectors representing the gradient of 
, and 
. A feasible direction must make an acute angle with each of these vectors. We start by plotting a vector representing 
and the vectors that are making an acute angle with it. Assume that 
is the vector 
. Two vectors that make a right angle with it are given by 
and 
, hence vectors that are making an acute angle with 
are between these two vectors. (Note the vectors that make a right angle with 
must have a product of zero with it, e.g., 
. This is illustrated below:
| > | Lg1:=plots[textplot]([1,2,`-grad(g1)`],align=ABOVE): |
| > | Neggradg1:=plots[arrow]({<1,2>,<-2,1>,<2,-1>}, width=[0.02, relative], head_length=[0.04, relative], color=red): |
| > | plots[display](Lg1,Neggradg1); |
 |
| > |
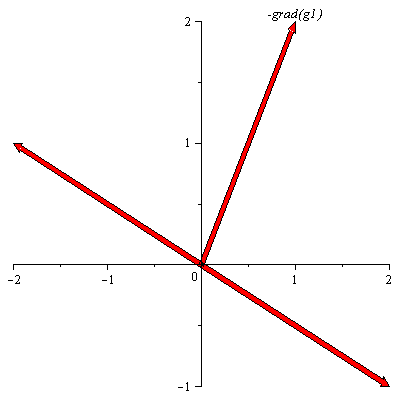The vectors that are making an acute angle with
are those that are between the two vectors making a right angle with it. These are the vectors with an end point above the red line (that passes via the origin).
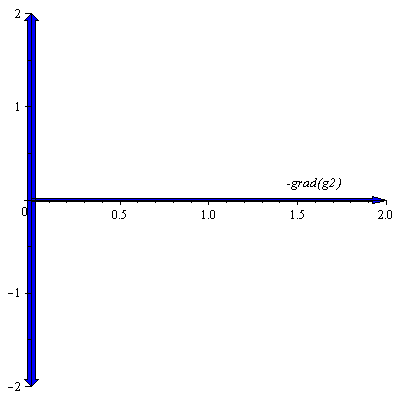
Assume that 
and let us now graph 
and all the vectors making an acute angle with it. This can still be displayed in the figure below.
| > | Neggradg2:=plots[arrow]({<2,0>,<0,-2>,<0,2>}, width=[0.02, relative], head_length=[0.04, relative],color=blue): |
| > | Lg2:=plots[textplot]([1.6,0.1,`-grad(g2)`],align=ABOVE): |
| > | plots[display](Lg2,Neggradg2); |
 |
| > |
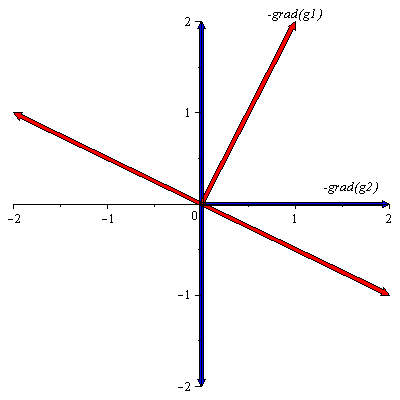
Let us now visualize the vectors that are making acute angles with both
and
This will be the intersection of the two sets of vectors described in the above two graphs. That is the vectors with an end point above the red line that passes via the origin, and to the left of the blue line that passes through the origin.
| > | plots[display](Lg1,Neggradg1,Lg2,Neggradg2); |
 |
| > |
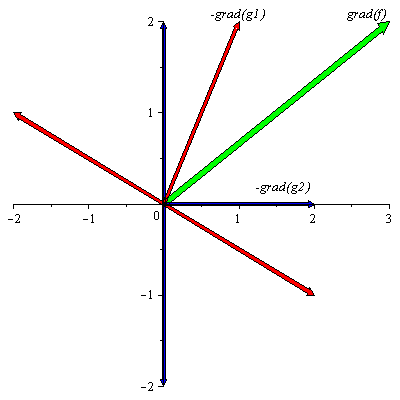
Recall that if 
is a minimum point, the angle between each feasible
and
must also be acute, that is 
for every 
which is a feasible direction. Observing the set of feasible directions in the graph above, the reader should realize that for
to make an acute angle with each feasible 
, 
must be between 
and 
An example of a vector that satisfies this condition is illustrated below. It is labeled as grad(f) and it is the green vector in the graph below:
| > | gradf:=plots[arrow](<3,2>, width=[0.02, relative], head_length=[0.04, relative],color=green): |
| > | Lf:=plots[textplot]([2.7,2,`grad(f)`],align=ABOVE): |
| > | plots[display](Lg1,Neggradg1,Lg2,Neggradg2,gradf,Lf); |
 |
| > |
However algebraically for 
to be between 
and 
it means that 
is a positive linear combination of 
and 
i.e., 
=
for some positive 
and 
In general therefore, this condition is satisfied if 
is a positive linear combination of 
, for 
such that 
. That is 
where the summation is over 
such that 
and the 
are all nonnegative. Footnote 8
We are now ready to stipulate the optimality conditions for the canonical minimization problem. It is common to stipulate the optimality conditions in terms of a function called Lagrangian, associated with the canonical optimization problem. The Lagrangian of our canonical minimization problem is defined to be a function of 
, a vector in 
(
is the number of constraints) and 
.
The optimality conditions are stated in terms of the partial derivative of the Lagrangian 
below:
i=1,...,n
j=1,...,m
j=1,...,m
The reader is asked to verify that the first condition above states that 
, the third condition ensures that if the 
constraint is not binding 
=0 and hence the sum in 
is only over the binding constraints. Finally the second constraint simply guarantees that 
is a feasible point and satisfies the constraints.
In our utility maximization problem, 
is 
, (
and 
are 
and 
), the non-negativity constraints on 
and 
can be written in terms of the 
, and we also have one inequality constraint that can be written as an equality constraint 
because of the monotonic of 
. The equality constraint can be written as two inequality constraints.
The reader is asked to show that this will alter the optimal conditions only by allowing the 
associated with this constraint to be positive or negative instead of the nonnegative constraint that is imposed on λ that is associated with an inequality constraint of the type less than or equal. Our problem is a maximization problem. We can transform the maximization of 
to a minimization of 
. Therefore we have
s.t. 
Writing the Lagrangian of this problem and the optimality conditions where, 
and 
are associated with
the non-negativity constraints on 
and 
respectively, yields:
+
c
=
=
=
c
c
If we assume that the non-negativity constraints on 
and 
are not binding, that is that the optimal solution is an interior point of the positive orthant we can try to satisfy the equations:
which implies that
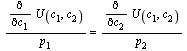
or that
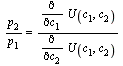
Note that 
is the slope of the budget line and
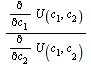is the slope of the indifference curve. Since 
we have the second equation:
Solving these two equations will thus produce the same solution as produced by the graphical procedure.
We conclude this chapter with an example. Consider the optimization problem
s.t. 
Where 
, 
, 
and 
. The KT optimality conditions of this problem are:
This system of equalities and inequalities can be solved by Maple as demonstrated below.
| > | solve({c1+c2/(1.14)=80,-diff(c2+1.07*c1,c1)+lambda+eta||1=0,\
-diff(c2+1.07*c1,c2)+lambda*(1/1.14)+eta||2=0,\ c1>=0,c2>=0,eta||1<=0,eta||2<=0,eta||1*c1=0,eta||2*c2=0},\ {c1,c2,lambda,eta||1,eta||2}); |
 |
| > |
One of the exercises at the end of the chapter asks the reader to solve this problem using the graphing approach (which can also be done using our procedure BudnIndif(c1+c2/1.14, c2+1.07c2)) and to explain and compare the results of the graphical approach with that of the formal approach using KT conditions.