Feynman's sum over paths method for Fraunhofer scattering

The sum over paths method is used to produce the single-slit diffraction pattern. The idea is that photons can take all kinds of possible paths which connect the source with a point on the screen. We can illustrate this idea by considering straight-line paths between the source and a point y(i) somewhere in the aperture. We subdivide the aperture in equally spaced intervals according to the following scheme:

> restart;

> N:=40; # the number of paths

> a:=10; # the slit width in wavelengths

> y_i:=i->evalf(a/2-(i-1/2)*a/N); # a subdivision of the aperture

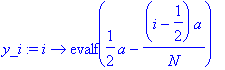
> y_i(1),y_i(N/2),y_i(N/2+1),y_i(N);

We have chosen N paths through the aperture at equidistant heights. We choose a distance between source and aperture (called X), we use this same distance between aperture and screen, and use the variable Y to denote how far away from the center position we are on the screen. All these distances are measured in wavelength (this is of the order of microns or less).

> X:=500; # the source-screen and screen-aperture distance

> Y:='Y';

The distance travelled by a photon along one of these paths is given by two contributions:

source to aperture: sqrt(X^2 + y_i^2)

aperture to screen: sqrt(X^2 + (y_i-Y)^2)

> d_i:=(i,Y)->sqrt(X^2+y_i(i)^2)+sqrt(X^2+(y_i(i)-Y)^2);

> t_i:=i->d_i(i)/c;

> f:=c/lambda;

Feynman's idea to explain the phase: think of the photon travelling along the straight-line path with a clock whose handle shows how much time has passed. The photon oscillates with a frequency which depends on the wavelength (color) of the light. All we need to know is the orientation of the clock handle at the end of the path, when it hits the screen. Technically this determines the phase (in phasor language we determine whether the wavelet that travelled along this path arrives with a crest or a through, i.e., with what amplitude).

To determine the phase: we want exp(I*2*Pi*f*t_i)

We realize that c drops out, and that we need a distance divided by wavelength, i.e., the distance measured in multiples of the wavelength .

Then we add up all the phases, i.e., we add the clock handles in the sense of vector addition. It is an addition of complex numbers of equal modulus (magnitude). This gives us the probability amplitude with which the wave arrives. The squared modulus (magnitude) of this number gives us the light intensity at the point Y.

Let us illustrate how this vector addition works using little arrows (clock handles):

> with(plottools): with(plots):

Warning, the name changecoords has been redefined

> Y:=70;

> Lis:=[]: v0:=[0,0]:

> for i from 1 to N do: w1:=evalf(exp(2*Pi*I*d_i(i,Y))); v1:=[Re(w1),Im(w1)]; Lis:=[op(Lis),[arrow(v0,v0+v1,.2,.4,.1,color=red)]]: v0:=v0+v1; od: Lis:=[op(Lis),[arrow([0,0],v0,.2,.4,.1,color=blue)]]:

> display(seq(Lis[j],j=1..nops(Lis)),scaling=constrained);

Depending on the value of Y the arrows add up to form a long arrow, or they add up in such a way as to cancel contributions with a smaller resultant vector arrow. Explore the above diagram for different choices of Y !

Finally, we can write a function which carries out the phase (vectorial) addition

> A:=Y->add(evalf(exp(2*Pi*I*d_i(i,Y))),i=1..N);

> A(10);

> plot([seq([iY*2,abs(A(iY*2))^2],iY=-100..100)],style=point);

Exercise 1:

Investigate different cases of slit width a to wavelength ratios. Can you determine how the position of the first maximum scales? Consult a first-year physics textbook and check whether the results found in this worksheet agree with the formula for the diffraction maxima and minima given there.

Exercise 2:

Investigate to what extent the results depend on the chosen discretization of the aperture, i.e., vary the parameter N .

>