Harmonic oscillator animations

Martha Abell and James Braselton in their textbook Differential Equations with Maple V (Academic Press) provide some lines of code that allow to show movies of the mass-spring system by connecting straigh-line segments to depict a spring. The idea is to use the solution to the differential equation for the harmonic oscillator, y ( t ), which provides the location of the moving endpoint of the spring, i.e., the attached mass as a function of time. We begin by providing the solution to the differential equation.

The parameters are the mass and the spring constant, as well as the gravitational acceleration. We work implicitly in MKSA (SI) units, and pick values after the set-up of the equation and solution for the general case:

[ g is measured in m/sec^2, m in kg, k in N/m]

> with(plots):

> g:='g': m:='m': k:='k':

The forces acting on the mass are gravity (in the form F _ y = - mg , i.e., position-independent at the surface of the Earth), and the spring force given by Hooke's law, which counteracts the motion from equilibrium, F _H =- k ( y - y 0). If y is greater than y 0, the force accelerates in the negative y direction, and vice versa.

Note that one can make different kinds of springs: the usual springs encountered occasionally are tightly wound, and are to be stretched only (e.g., a slinky), but we know coil springs from car/motorcycle/bicycle suspensions that can be both stretched and compressed. With gravity present a tightly wound spring with a mass attached acquires an equilibrium point from which the spring can be both compressed and further stretched, i.e., the equilibrium point is no longer given as the length of the spring. The equilibrium point is determined as the point at which the gravitational attraction to the Earth's surface is balanced by the spring force which results from expanding the spring from its original equilibrium point to suspend the mass. We assume for simplicity that we have a stretch-only spring, which is idealized to be of zero length when totally compressed (natural state). The equilibrium position for the mass-spring system under gravity becomes (we label y 1 now as the height at which the system balances, the original balancing position that enters Hooke's law being y 0=0):

> y0:=0; y1:='y1':

> EQL:=-m*g-k*(y1-y0)=0;

> y1:=solve(EQL,y1);

We measure the displacement of the mass starting at y =0 (this being the equilibrium point without any mass attached) using the conventional direction (positive y is upwards). The gravitational acceleration therefore is F _ y =- mg . The Newton equation now reads:

> NE:=m*diff(y(t),t$2)=-m*g-k*(y(t)-y0);

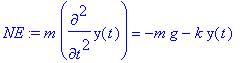
> sol:=dsolve(NE,y(t));

While every physics student definitely should be able to derive this general answer to the differential equation by hand, we assume that s/he can at least verify that the solution found by Maple is correct by substitution. We have two integration constants to be determined by the initial conditions. One typical condition is to release the system from rest at an arbitrary height. We could take the general solution, find the velocity expression by differentiation, and determine _C1 and _C2. Alternatively, we can specify the initial conditions, so that dsolve comes up with the special solution of interest. We pick some arbitrary height and zero velocity.

> IC:=y(0)=-0.2,D(y)(0)=0;

> sol:=dsolve({NE,IC},y(t));

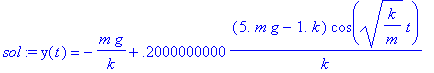
To plot we specify the constants:

> g:=10; m:=1; k:=10;

> Y_s:=unapply(rhs(sol),t):

We graph a stretch of 10 seconds together with the equilibrium position:

> y1;

> plot([Y_s(t),y1],t=0..10);

We recognize the simple harmonic motion about the equilibrium position. To graph a cartoon side view of the mass-spring system we need a sequence of straight-line segments. We pick a radius for the spring and the number of turns:

> w:=0.2: nT:=10:

Given a position for the mass y(t) we divide this length into 2 nT segments, and generate a list of points which alternate on the left and right.

> DL:=proc(t) local i,L,d; global w,nT;

> d:=evalf(Y_s(t)/(2*nT+1)); L:=[[0.,0.],[w,d*0.5]]:

> for i from 1 to nT do: L:=[op(L),[-w,d*(2*i-0.5)],[w,d*(2*i+0.5)]]; od: L:=[op(L),[0.,evalf(Y_s(t))],[w/4,evalf(Y_s(t))],[w/4,evalf(Y_s(t))-w/8],[-w/4,evalf(Y_s(t))-w/8],[-w/4,evalf(Y_s(t))],[0.,evalf(Y_s(t))]]; end:

> PL:=seq(plot(DL(j_t/10)),j_t=1..32):

> display(PL,insequence=true,axes=boxed);

There are many ways how one can make this problem more interesting:

1) introducing a friction term to make the problem realistic

2) to consider a friven harmonic oscillator.

Let us start with problem 1:

we need to add a term which is proportional to the velocity d y /d t . Whenever the velocity gets appreciable, we want a force that reduces it. For positive velocity it has to be negative, for negative velocity (downward) it has to be positive, i.e., we want a friction constant times the negative of the velocity added to the forces:

> b:='b': m:='m': g:='g': k:='k':

> NE:=m*diff(y(t),t$2)=-m*g-k*(y(t)-y0)-b*diff(y(t),t);

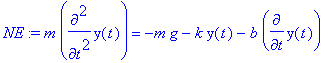
Using mathematical jargon we can say that this is still a non-homogeneous (due to the constant gravity-related term), second-order ordinary differential equation with constant coefficients. The method of solution is still the same [find the general solution to the homogeneous problem, (find and ) add a special solution to the inhomogeneous equation to the general homogeneous solution, and that is the general solution to the inhomogeneous problem with the boundary conditions still to be specified]. Maple still can do all the math work for us so we concentrate on understanding the physics:

> sol:=dsolve(NE,y(t));

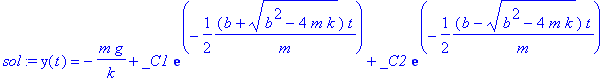
The solution is expressed in a 'weird' way if we expect oscillatory answers, but keep in mind that the exponentials may turn out to have imaginary arguments. In fact, the damped HO admits both oscillatory and non-oscillatory solutions (depending on the strength of the damping).

Let us put in the same initial conditions as before:

> sol:=dsolve({NE,IC},y(t));

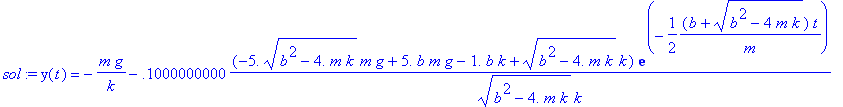
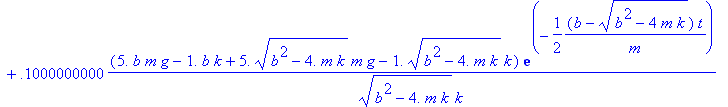
Let us pick a small value for the damping coefficient in addition to the previously chosen parameters [the units for b : Ns/m]:

> g:=10; m:=1; k:=10; b:=1/5;

> Y_s:=unapply(rhs(sol),t):

> plot([Y_s(t),y1],t=0..20);

Voila, the solution is oscillatory.

> PL:=seq(plot(DL(j_t/10)),j_t=1..320):

> display(PL,insequence=true,axes=boxed);

We can think of real-life applications:

The shock absorbers in a car's (or other vehicle's) suspension system cooperate with the coils (or other springs, such as multi-link suspension, or leaf springs) to provide a damped oscillator. In fact, one is not interested in the kind of motion displayed above, but would rather want to absorb the oscillatory energy in one-two swings. From the analytic form of the solution in the case with unspecified constants we can see when a character change occurs in the solution. This character change occurs as b ^2-4 km turns zero, and the exponential has no longer complex-valued arguments [we add a tiny number to avoid a zero denominator]:

> g:=10; m:=1; k:=10; b:=sqrt(4*k)+10^(-Digits);

> Y_s:=unapply(rhs(sol),t):

> plot([Y_s(t),y1],t=0..10);

This case is called the critically damped solution.

There are interesting questions to be asked, such as: what happens if the damping is increased further? Is it desirable to do so in applications?

Let us double the damping:

> g:=10; m:=1; k:=10; b:=2*sqrt(4*k)+10^(-Digits);

> Y_s:=unapply(rhs(sol),t):

> plot([Y_s(t),y1],t=0..10);

We see that it takes longer for the spring-mass system to reach equilibrium! One has introduced so much friction that it takes forever to reach the final height.

There is an interesting representation that allows to gain further insights. In a so-called phase-space diagram one plots the velocity versus the position with time playing the role of the parameter. This curve [an abstract object called the phase-space trajectory] allows to read off how energy is dissipated in the system. For the case without friction it results in a closed curve. Solutions with different initial conditions are characterized by similar-looking phase-space trajectories whose size is a measure of the amount of total energy which is conserved and transformed between kinetic and potential energy forms. For the case with damping we obtain spirals, as energy is removed from the system.

Let us begin with undercritical damping.

> g:=10; m:=1; k:=10; b:=1/2;

> Y_s:=unapply(rhs(sol),t):

> V_s:=D(Y_s);

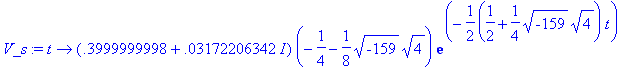
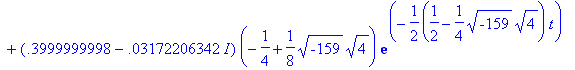
> plot([Y_s(t),V_s(t),t=0..20]);

Due to the small amount of damping it may not be immediately obvious, but we wish to point out that the reduction in mechanical energy (reduction of radius) occurs during those phases when the magnitude of the velocity is largest. This can be inferred from a careful inspection of the graph, or from a detailed plot of the total energy as a function of time:

> Etot:=t->1/2*m*V_s(t)^2+m*g*Y_s(t)+1/2*k*Y_s(t)^2;

> plot([Etot(t)-Etot(0),V_s(t)],t=0..5);

We leave it as an exercise to look at the diagrams for the critically and overcritically damped cases.

Now we turn to the case of a driven HO. We choose a harmonic driving force with small amplitude to drive the HO away from the equilibrium. A circular frequency nu characterizes the driving force.

> b:='b': m:='m': g:='g': k:='k': nu:='nu':

> NE:=m*diff(y(t),t$2)=-m*g-k*(y(t)-y0)-b*diff(y(t),t)+(1/10)*sin(nu*t);

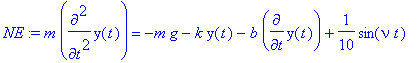
For the undamped case the internal frequency of the oscillator is:

> omega:=sqrt(k/m);

We need to investigate what happens as nu is varied over a wide range, and particularly what happens as nu approaches omega (resonance).

For a small amplitude of the driving force we can expect dramatic results only for nu close to omega.

> g:=10; m:=1; k:=10; b:=1/2;

> omega;

> y1;

> nu:=3.1;

> sol:=dsolve({NE,y(0)=y1,D(y)(0)=0},y(t)):

The result is long, and perhaps worth looking at.

> Y_s:=unapply(rhs(sol),t):

> plot([Y_s(t),y1],t=0..20);

It is worthwhile to repeat the calculation for different values of nu, and to observe the more complicated transient behaviour. Eventually the system responds with oscillations at the driving frequency nu. This latter fact is clearly evident when choices are made for nu quite different from omega. On the other hand, we obtain appreciable oscillations only near resonance.

The phase-space diagram shows that the abstract phase-space trajectory approaches a limit cycle:

> V_s:=D(Y_s):

> plot([Y_s(t),V_s(t),t=0..20]);

The emergence of a limit cycle tells us that there comes a point when as much energy is dumped into the mass-spring system by the driving force, as there is energy lost due to friction. We encourage the student to try out cases where the friction is smaller, and therefore, larger-amplitude motion can be observed. We also leave it as an exercise to explore different driving force frequencies.

To complete the understanding of the driven HO with damping one has to figure out the dependence of the final amplitude on the frequency of the driving force.

> b:='b': m:='m': g:='g': k:='k': nu:='nu':

> NE:=m*diff(y(t),t$2)=-m*g-k*(y(t)-y0)-b*diff(y(t),t)+(1/10)*sin(nu*t);

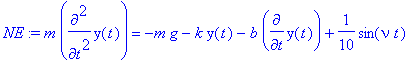
> y1;

> sol:=dsolve({NE,y(0)=y1,D(y)(0)=0},y(t)):

> Y_s:=unapply(rhs(sol),t);

>

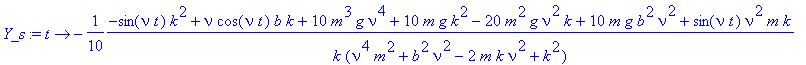
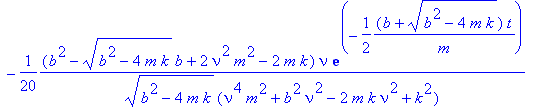
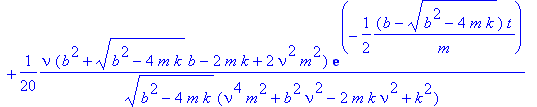
Intuitively it is clear that for undercritical damping the internal oscillations die out on a time scale determined by the damping constant b . What remains is the first term in the above expression whose time variation is just connected to the inhomogeneous term in the Newton equation, i.e., just to the periodic driving force.

Let us assume that we are in the asymptotic regime, which is reached when exp(- bt /2 m ) becomes negligible compared to the first term. We simply pick out the first term in the solution. For our choice of b =1/2 (a strong, but undercritical damping) t _a=20 should be appropriate. We can verify from a graph, that we have reached the limit cycle, i.e., driven harmonic motion with constant amplitude.

> Y_as:=unapply(op(1,Y_s(t)),t);

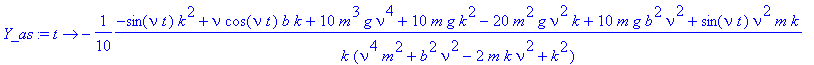
> plot([subs(g=10,m=1,k=10,b=1/2,nu=31/10,Y_as(t)),subs(g=10,m=1,k=10,y1)+1/20*sin(31/10*t)],t=20..40,color=[red,blue]);

The graph shows that the harmonic motion associated with the limit cycle is centered on the equilibrium point y 1, and is phase shifted compared to a simple sin(nu* t ). The phase shift is achieved by the combination of sines and cosines present in the solution.

Our interest is in extracting the amplitude as a function of the parameters. First we have to subtract the equilibrium position:

> assume(nu,real);

> A:=combine(Y_as(t)-y1,trig);

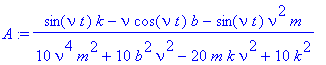
> A0:=simplify(subs(b=0,A));

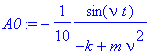
We note that in the case without friction the asymptotic amplitude blows up on resonance [note that omega^2= k / m ]. This means that no limit cycle is reached, but that the amplitude grows linearly with time [the latter detail is obtained from an analysis of the solution to Newton's equation, we leave it as an exercise to extract this result].

For the case with friction the resonance occurs at a shifted frequency, and the mentioned phase shift occurs. Let us look first at the asymptotic solution when nu is chosen to be on resonance in the frictionless (undamped HO) case. This answer should be reasonable for small friction constants b .

> simplify(algsubs(nu=sqrt(k/m),A));

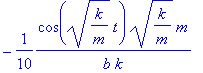
So let us assume that near resonance the amplitude is given by looking just at the cosine term (as the two sine terms nearly cancel on resonance in the weakly damped case).

> A1:=simplify(nu*b*cos(nu*t)/denom(A));

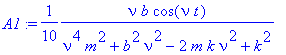
For the amplitude of oscillation we have:

> A1a:=simplify(nu*b/denom(A));

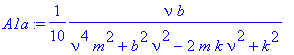
Now we specify k and m , with the resonance at omega=sqrt(10).

> A1as:=subs(m=1,k=10,A1a);

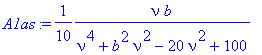
> P0:=plot([sqrt(10),t,t=0..1.5],color=black):

> P1:=plot(subs(b=1/5,A1as),nu=3..3.3,color=red):

> P2:=plot(subs(b=1/15,A1as),nu=3..3.3,color=blue):

> P3:=plot(subs(b=1/45,A1as),nu=3..3.3,color=green):

> display(P0,P1,P2,P3,axes=boxed,labels=[frequency,Amplitude]);

The graph shows that the damped oscillator is capable of absorbing energy from the driving mechanism in the following way:

1) very weak damping: the oscillator can only absorb energy effectively if the mechanical energy is offered at a frequencies close to the natural frequency, which is very close to the natural frequency of the undamped oscillator;

2) for moderate damping the range over which energy can be absorbed broadens somewhat; the resonance condition is shifted slightly towards lower frequencies when compared to the undamped natural frequency.

3) for stronger damping the resonance is broadened: the harmonic oscillator is able to absorb frequencies over a wider range equally, but the amplitude of oscillation is reduced considerably. This is the result of the driving force not being able to be in phase with the internal oscillatory motion even in the asymptotic regime.

For a more detailed analysis the reader may wish to consult the book by Ron Greene: Classical Mechanics with Maple (Springer-Verlag).

>