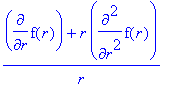
Poisson equation

We solve the Poisson problem in cylindrical coordinates to find the variation of electrostatic force and potential with radial distance between two concentric cylinders in the presence of a charge cloud at the cathode (the inner cylinder which represents a heated filament). For the case withoud the charge cloud we solved Laplace's equation with the boundary condition that the potential is held constant ( V ( l )=0 at the inner cylinder, i.e, the filament of a diode, and V ( d )= V 0 at the anode cylinder). This was done in the worksheet Laplace.mws . Our interest here is to take the electron plasma in a diode into account, i.e., once the filament is heated and a current flows, such that there is a stable equilibrium. The electronic charge cloud develops its own potential which can impede the flow of current (space-charge-limited region of the current-voltage characteristic). We attempt to solve precisely this part of the problem in the present worksheet.

We need to solve the equation given in Cartesian coordinates as

diff(V,x$2)+diff(V,y$2)+diff(V,z$2) = 4*Pi*rho(x,y,z)

The problem reduces to one dimension in cylindrical coordinates.

> restart; with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

Maple can remind us of the Laplacian in various orthogonal coordinate systems (without explicit computations). We are interested in the radial part only:

> v1 := [r, theta, z]:
laplacian(f(r), v1, coords=cylindrical);

We need to make some assumptions about the radial distribution of the charge cloud. A heated filament results in a constant flow of charge in and out of the filament to avoid a net charge on it. If an electric field is applied between the anode (outer cylinder) and cathode (filament), then one has an electron charge density that extends between both cylinders. We will not attempt to model a self-consistent situation, but rather calculate the electrostatic repulsion originating from an assumed charge cloud. We simply assume an exponential distribution:

> rho0:=1;

> rho:=rho0*exp(-r/10);

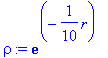
This is a surface density really, as we do not take into account what happens along the z axis.

> evalf(2*Pi*int(rho*r,r=1..100));

This is the total amount of charge. It is controlled by the heating current of the filament. At higher temperatures (more heating current) a larger number of electrons will overcome the work function. The electrons are assumed to be distributed in an exponential fashion (this means that in principle some of them reach the anode at a distance of 100 filament radii. (This results in the diode acting as a battery when the filament is heated).

> evalf(2*Pi*int(rho*r,r=1..infinity));

We formulate Poisson's equation:

> DE:=diff(V(r),r$2)+diff(V(r),r)/r=rho;

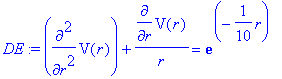
This differential equation has a solution that combines the result from the density-free case (which is incorporated through the boundary condition which specifies the potential) and the electron-electron repulsion:

> dsolve(DE,V(r));

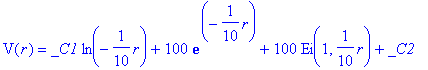
The boundary conditions of zero potential at the filament and potential V0 at the cylinder can be imposed, but the thickness of the filament has to be taken into account due to the log-divergence at r =0.

> BC:=V(l)=0,V(d)=V0;

> sol:=dsolve({DE,BC},V(r));

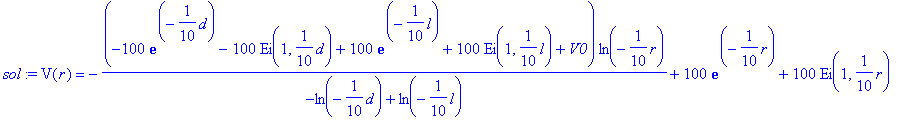
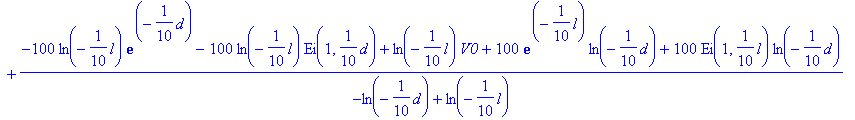
> Vp:=simplify(rhs(sol));

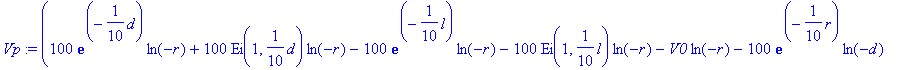
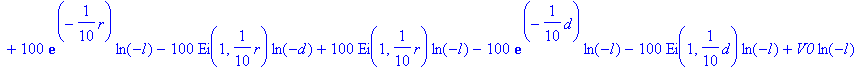
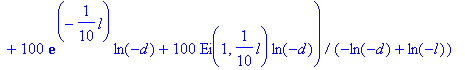
The solution is in terms of the exponential integral. Maple can evaluate it numerically:

> evalf(subs(l=1,d=100,V0=100,r=2,Vp));

The above result shows that we need to remove the imaginary part in order to graph the result:

> plot([subs(l=1,d=100,V0=100,Re(Vp)),10*r*rho],r=1..100,color=[red,blue]);

The result shows what happens due to the presence of the electron cloud: the potential does not interpolate in a simple way between V =0 at the cathode and V = V 0 at the anode. The electrostatic repulsion has the effect that only the electrons in the tail region of the density profile experience an attraction towards the anode.

Note that we have shown r*rho (multiplied by an arbitrary scale factor) rather than the density itself. This quantity provides a measure of how much charge is found in a circular shell at radius r (between r and r+dr ) .

The radial component of the electric field is calculated as follows:

> E:=-diff(Vp,r);

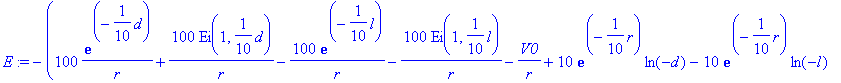
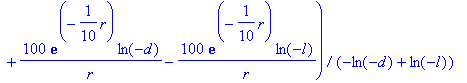
We graph the radial force acting on an electron ( F = qE , with q =-1) using as a distance scale the filament radius l , and assume that the anode cylinder has a radius d of 100 times the filament radius.

> plot(subs(l=1,d=100,V0=100,-E),r=1..100);

The force due to the electron-electron repulsion pushes the nearby electrons back into the filament (a stable density can be maintained if the heating mechanism ejects as many electrons as are re-absorbed). The electron-electron repulsion potential overshadows the electric field due to the applied external voltage for distances out to 10-15 filament radii.

Exercise 1:

Explore what happens when one reduces (increases) the electron charge by varying (i) the factor rho0 ; (ii) the factor controlling the fall-off of rho(r) .

What are the implications for the current-voltage characteristic of a diode (vacuum tube)?

Exercise 2:

Repeat the calculation for a Gaussian shape of the radial electron distribution.

Other examples of charge densities for which the potential can be readily calculated in terms of elementary functions are bell-shaped functions of the type 1/(a^2+r^2)^n .

>