The work integral in classical mechanics

Let us demonstrate the path independence of the work integral for a conservative curl-free force field,

such as the gravitational field of a sphere.

Let us define the potential energy for a particle of mass m in the field of the star (or planet) of mass M .

> V:=-G*M*m/r;

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> F:=-grad(V,[x,y,z]);

That didn't work!

> F:=-grad(V,[r,theta,phi],coords=spherical);

> evalm(F[1]);

The - sign on front of the grad throws Maple off, because the grad procedure returns a vector, and not a list. The fix is to put the minus sign with the scalar potential function V.

> F:=grad(-V,[r,theta,phi],coords=spherical);

> F[1];

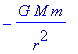
OK, Maple has its peculiar features! It didn't like the '-' sign before the gradient.

> curl(F,[r,theta,phi],coords=spherical);

The force field is curl-free by construction: it has been derived from a scalar potential.

For plotting the potential energy we need to switch to Cartesian coordinates. We choose the show the potential at a fixed z=1 plane:

> PL1:=plot3d(subs(r=sqrt(x^2+y^2+1),G=1,M=1,m=1,V),x=-5..5,y=-5..5,axes=boxed): plots[display](PL1);

Let us choose a straight-line path:

> r_i:=[2,2,1];

> r_f:=[-2,0,1];

> r_t:=r_i+(r_f-r_i)*t;

> evalm(r_t);

Note: here t is a parameter, not necessarily time. Nevertheless, we call the derivative of the parameter representation v _t:

> v_t:=diff(r_t,t);

Now the work integral is reduced to a parameter integral using the dotproduct of F with v _t, but also realizing that F needs to be evaluated along the path,

i.e., as F ( r _t) !!!

Also: we have defined the parameter representation in Cartesian coordinates, so we should use these coordinates for the dot product calculation, which means that the force has to be translated into Cartesians. How do we do this?

> F:=grad(-subs(r=sqrt(x^2+y^2+z^2),V),[x,y,z]);

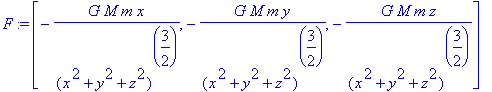
We start with the common mistake made by many beginners:

> Work:=int(dotprod(F,v_t),t=0..1);

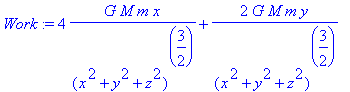
This is a bad answer for several reasons:

1) the work has to come out as a number (we have specified initial and final points).

2) we have not evaluated the force along the chosen path.

> r_t:=evalm(r_t);

> Work:=int(dotprod(subs(x=r_t[1],y=r_t[2],z=r_t[3],F),v_t),t=0..1);

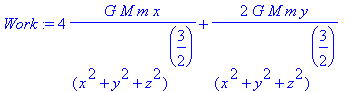
This is frustrating: we do apparently the right thing, yet we get the same wrong answer!!!

How do we avoid this pitfall?

1) look at subexpressions, and then realize that something hasn't worked.

Substitutions into vectors and matrices in Maple require the use of the op():

> dotprod(subs(x=r_t[1],y=r_t[2],z=r_t[3],op(F)),v_t);

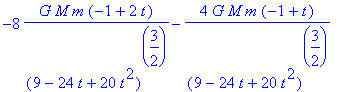
This is the correct integrand: it no longer depends on x , y , z just on the parameter t .

Now do the integral:

> Work:=int(dotprod(subs(x=r_t[1],y=r_t[2],z=r_t[3],op(F)),v_t),t=0..1);

An alternative to using op() is to convert the vector produced by grad into a list.

> FL:=convert(F,list);

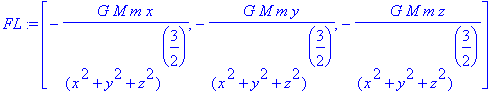
> Work:=int(dotprod(subs(x=r_t[1],y=r_t[2],z=r_t[3],FL),v_t),t=0..1);

> evalf(%);

The work integral tells us by how much the kinetic energy has changed between r _i and r _f due to the work done by the force on mass m .

Now let us compare this result with the potential energy difference:

> r_i;

We need a function to calculate the magnitude of the position vector:

> v_mag:=v->sqrt(add(v[i]^2,i=1..3));

> v_mag(r_i),v_mag(r_f);

> subs(r=v_mag(r_i),V)-subs(r=v_mag(r_f),V);

We recognize that the difference between the potential energy at the initial and final points amounts to the same as the work done on the particle, or the change in kinetic energy.

> Work-%;

> with(plottools);

> l := line(r_i, r_f, color=red, linestyle=2, thickness=3): plots[display](l,PL1);

We want to indicate with the height the amount of potential energy, therefore:

> r_iV:=r_i: r_iV[3]:=subs(r=v_mag(r_i),G=1,M=1,m=1,V): r_iV;

> r_fV:=r_f: r_fV[3]:=subs(r=v_mag(r_f),G=1,M=1,m=1,V): r_fV;

> l := line(r_iV, r_fV, color=red, linestyle=2, thickness=3): plots[display](l,PL1);

As the particle traverses the potential well it picks up a lot of kinetic energy on the way down, in order to give up a good fraction as it climbs up the hill.

We can verify this by calculating the work done at some intermediate point.

First recall the total kinetic energy gain:

> evalf(Work);

Now break the path up into two halves, just by looking at what happens between t =0 and t =0.5, and then between t =0.5 and t =1:

> Work1:=int(dotprod(subs(x=r_t[1],y=r_t[2],z=r_t[3],op(F)),v_t),t=0..1/2);

> Work2:=int(dotprod(subs(x=r_t[1],y=r_t[2],z=r_t[3],op(F)),v_t),t=1/2..1);

> evalf([Work1,Work2,Work1+Work2]);

Notice the large amount of work done on the particle on the first 'half', then the particle works against the potential well, but still has a net gain of kinetic energy at the final point. It is, however, at a lower value of potential energy at this point, i.e., it gained kinetic energy at the expense of potential energy.

Now consider a non-conservative force. It will have no direct physical meaning, i.e., it is a made-up problem to demonstrate what happens when a force field is not conservative.

> restart;

> F:=[x^2+2*y-z,y+z-x,z^3+x*2];

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> curl(F,[x,y,z]);

This force field is not curl-free, which means that it cannot be derived from a scalar potential. We choose the same path as before.

> r_i:=[2,2,1];

> r_f:=[-2,0,1];

> r_t:=evalm(r_i+(r_f-r_i)*t);

> v_t:=diff(r_t,t);

Another one of these Maple-quirks. We defined r_t as a combination of lists, but the evalm did something funny.

> whattype(r_t);

The evalm turned r_t into a symbol.

> v_t:=map(diff,r_t,t);

If we had avoided the evalm , the simple differentiation would have worked because t appeared as a factor of one of the lists (as carried out in the previous section).

> Work1:=int(dotprod(subs(x=r_t[1],y=r_t[2],z=r_t[3],F),v_t),t=0..1/2);

> Work2:=int(dotprod(subs(x=r_t[1],y=r_t[2],z=r_t[3],F),v_t),t=1/2..1);

> Work:=int(dotprod(subs(x=r_t[1],y=r_t[2],z=r_t[3],F),v_t),t=0..1);

> evalf([Work1,Work2,Work1+Work2,Work]);

Of course, the work integral is additive. What we want to demonstrate is that if we connect the two endpoints in some different way, then a different result will be found for the work done on the particle as it moves from A to B.

Let us choose as an alternative to the direct connection from A to B a path that goes via the origin [0,0,1] in the plane.

> r_1:=[0,0,1];

> r_tp1:=evalm(r_i+(r_1-r_i)*t);

> v_tp1:=map(diff,r_tp1,t);

> r_tp2:=evalm(r_1+(r_f-r_1)*t);

> v_tp2:=map(diff,r_tp2,t);

Now we are ready to calculate the work integral.

> Work1:=int(dotprod(subs(x=r_tp1[1],y=r_tp1[2],z=r_tp1[3],F),v_tp1),t=0..1);

> Work2:=int(dotprod(subs(x=r_tp2[1],y=r_tp2[2],z=r_tp2[3],F),v_tp2),t=0..1);

> evalf([Work1+Work2,Work]);

The amount work done on the particle as it moves through the force field along a different path is different!

What can we do to visualize the force field, and how it affects the particle?

First define the force field in the z =1 plane and ignore the z-component of the force, as we are not moving the particle along z (no work is done by this component of the force!).

> Fzeq1:=subs(z=1,F);

> F2d:=[Fzeq1[1],Fzeq1[2]];

> with(plots):

Warning, the name changecoords has been redefined

> PL1:=fieldplot(F2d,x=-2..2,y=-2..2,arrows=thick,color=blue,axes=boxed,grid=[12,12]): display(PL1);

> with(plottools):

> l1 := line([r_i[1],r_i[2]], [r_f[1], r_f[2]], color=red, linestyle=2, thickness=3):

> l2 := line([r_i[1],r_i[2]], [r_1[1], r_1[2]], color=green, linestyle=2, thickness=3):

> l3 := line([r_1[1],r_1[2]], [r_f[1], r_f[2]], color=green, linestyle=2, thickness=3):

> display(l1,l2,l3,PL1);

The amount of work done on the particle as it moves through this field is different, because in different regions of space the the force vectors are allowed to have different lengths and different orientations.

For a force field which is not curl-free, the travel over a closed contour (loop) allows one to gain (or lose) energy.

The graph also shows visually why we refer to the field as not being curl-free.

> evalf([Work1,Work2,Work1+Work2,Work]);

Note that the amount of work done by the force on the particle is negative. We start the particle at [2,2] (top right-hand corner), and it moves against the force field.

The fact that it arrives at location [0,-2] with a negative amount of work (it worked against the force field) means that its kinetic energy will be less than it was at A. It will be less at B than at A by a different amount depending on whether the red or green path is chosen.

An interesting question:

Exercise:

Calculate the work done on the particle along a path such that it gains energy to go from A=[2,2,1] to B=[-2,0,1].

>

Solution