If it was so, it might be; and if it were so, it would be; but as it isn't, it ain't. That's logic.

Lewis Carroll [ quoted in Fallacies in Science ]

Topics

• To get a fairly dramatic sense of what this lecture is about, consider the following three images, taken from cognitive psychologist Michael McCloskey's   Naive Theories of Motion, in D Gentner and A L Stevens, eds., Mental Models (Hillsdale, NJ: Erlbaum, pp. 299-324, 1983). Similar images appear also in McCloskey's 1983 article in Scientific American (see Readings, Resources and Questions below).

   

  

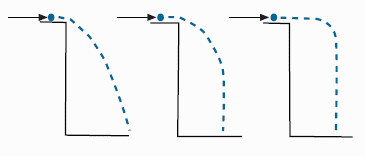
  The Cliff Problem

   

   

  

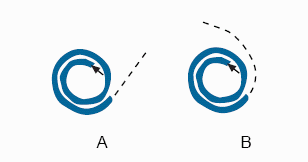
  The Spiral Tube Problem

   

   

  

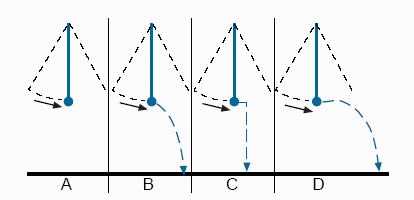
  The Pendulum Problem

   

  Although they may first seem rather abstract, these images refer to very familiar situations: an object falling from a table, water spurting out of a coiled hose, a kid jumping off a swing. Test yourself: in each picture, which alternative corresponds to what actually happens? Some of you may be surprised by the answer. Not to spoil your surprise, we will carry out the test in class. If you picked the wrong answer, console yourself with the knowledge that your answer has a very long history that goes back at least to the Middle Ages, and arguably even farther back.

   

  

  Impetus Theory in the Field, According to Walther H Ryff (1582)

   

  McCloskey and others have described many similar situations. Here is one:

  "Imagine the following situation. A person is holding a stone at shoulder height while walking forward at a brisk pace. What will happen if the person drops the stone? What kind of path will the stone follow as it falls?
  Many people to whom this problem is presented answer that the stone will fall straight down, striking the ground directly under the point where it was dropped. A few are even convinced that the falling stone will travel backward and land behind the point of its release. In reality the stone will move forward as it falls, landing a few feet ahead of the release point. Newtonian mechanics explains that when the stone is dropped, it continues to move forward at the same speed as the walking person, because (ignoring air resistance) no force is acting to change its horizontal velocity. As the stone travels forward it also moves down at a steadily increasing speed. The forward and downward motions combine in a path that closely approximates a parabola."
  [ from M McCloskey, Intuitive Physics, Scientific American, 248, 122-130 (April 1983) ]

• It is indeed rather surprising that such misconceptions are so widespread (tests have shown that even students about to complete their PhD in physics are not immune from them). This is where history can help us. These misconceptions, according to McCloskey (and many others) "appear to be grounded in a systematic, intuitive theory of motion that is inconsistent with the fundamental principles of Newtonian mechanics. Curiously, the intuitive theory resembles a theory of mechanics that was widely held by philosophers in the three centuries before Newton."[ Mc Closkey, op. cit. ]
  This medieval theory is called the theory of impetus, and was in turn a medieval variation on Aristotle's account of motion. Here is how John Buridan (1295/1305 – 1358/61) describes his version of the theory:

  "When a mover sets a body in motion he implants into it a certain impetus, that is, a certain force enabling a body to move in the direction in which the mover starts it, be it upwards, downwards, sidewards, or in a circle. The implanted impetus increases in the same ratio as the velocity. It is because of this impetus that a stone moves on after the thrower has ceased moving it. But because of the resistance of the air (and also because of the gravity of the stone) which strives to move it in the opposite direction to the motion caused by the impetus, the latter will weaken all the time. Therefore the motion of the stone will be gradually slower, and finally the impetus is so diminished or destroyed that the gravity of the stone prevails and moves the stone towards its natural place. In my opinion one can accept this explanation because the other explanations prove to be false whereas all phenomena agree with this one." [ from Impetus Theory ]

  In other words, impetus was considered a special substance that was injected into an object when set in motion and determined the specifics of its motion, just as phlogiston was supposed to be a special fluid substance that characterized all flammable materials. Notice also Buridan's use of the notion of "natural place." This is straight from Aristotle.
• As McCloskey writes, "what is difficult to understand is why people develop incorrect beliefs about the trajectories of moving objects, beliefs that apparently conflict with everyday experience. Why, for example, do people come to believe carried objects fall straight down when they are dropped?"

  "A possible answer is that under some conditions the motion of objects is systematically misperceived. Washburn, Linda Felch and I have proposed that objects dropped from a moving carrier are often perceived as falling straight down. The misperception may be the source of the corresponding belief that they do so. Studies in the perception of motion have shown that when an object is viewed against a moving frame of reference, a visual illusion can arise. The motion of of the object relative to the moving frame of reference can be misperceived as absolute motion (that is, as motion relative to the stationary environment). For example, if a dot in the interior of a rectangle remains motionless as the rectangle moves to the right, the dot can be perceived as moving to the left [see The Perception of Motion, by Hans Wallach, Scientific American, July 1959] [ … ] How can such misconceptions be dispelled? The most obvious answer is through normal instruction in Newtonian mechanics, but studies by several investigators suggest that the intuitive ideas are difficult to modify. Although some students who take physics courses achieve a firm grasp of Newtonian mechanics, many emerge with their intuitive impetus theories largely intact." [ Mc Closkey, op. cit. ]

  It is interesting to note that even Galileo Galilei (1564 - 1642), in his early work, fell in the impetus trap. The fact is that it is not easy, especially with the instruments available in those times, to carry out measurements of moving bodies with sufficient precision to establish how bodies, such as, say, a ball falling off a table, actually move. Eventually Galileo solved the problem with an idea which is as simple as it is brilliant: he reduced the speed to a value easily measurable by letting the ball roll down an inclined plane. See, e.g., The Medieval Impetus Theory, and/or Galileo's Analysis of Projectile Motion.
• Cognitive illusions extend well beyond the realm of physics. McCloskey, for example, has continued his work discovering fundamental cognitive fallacies in many areas of economics, particularly in decision making. It is important to mention in this regard the pioneering work of D Kahneman, P Slovic and A Tverski, published in Judgment Under Uncertainty: Heuristics and Biases, Cambridge University Press, 1982. As a starting point, however, you may want to read Smart Heuristics: Gerd Gigerenzer:

  "The fact that people ignore information has been often mistaken as a form of irrationality, and shelves are filled with books that explain how people routinely commit cognitive fallacies. In seven years of research, he, and his research team at Center for Adaptive Behavior and Cognition at the Max Planck Institute for Human Development in Berlin, have worked out what he believes is a viable alternative: the study of fast and frugal decision-making, that is, the study of smart heuristics people actually use to make good decisions. In order to make good decisions in an uncertain world, one sometimes has to ignore information. The art is knowing what one doesn’t have to know."

  For something a bit closer to home, read   Clarification of Selected Misconceptions in Physical Geography, a very interesting paper by B D Nelson, R H Aron, & M A Francek, which appeared in Journal of Geography, 91 (2) 76-80 (1992), or a review by Laura Henriques,   Children's Misconceptions About Weather, a paper presented at the annual meeting of the National Association of Research in Science Teaching, New Orleans, LA, April 29, 2000. See also Palmerini's book, referenced under Readings, Resources and Questions below, for a broad range of examples from everyday life.
• Finally, I should mention logical fallacies. Two excellent resources are Stephen's Guide to the Logical Fallacies, and Real-World Reasoning: Informal Logic for College, a marvelous course taught by Peter Suber at Earlham College. Both resources include extensive references and links.
  We can barely scratch the surface of this important area. To emphasize how important it is, I will ask you to begin exploring the so-called prisoner's dilemma. A good starting point is You Have Found The Prisoners' Dilemma, where you can also play the game.

  "Prisoners' Dilemma is a game which has been and continues to be studied by people in a variety of disciplines, ranging from biology through sociology and public policy. Among its interesting characteristics are that it is a 'non-zero-sum' game: the best strategy for a given player is often one that increases the payoff to one's partner as well. It has also been shown that there is no single 'best' strategy: how to maximize one's own payoff depends on the strategy adopted by one's partner. Serendip uses a particular strategy (called 'tit for tat') which is believed to be optimal under the widest possible set of partner strategies."

  So, what is the prisoner's dilemma? The webpage above spells it out quite clearly. Here I will give Wikipedia's different, but equivalent formulation:

  "Two suspects are arrested by the police. The police have insufficient evidence for a conviction, and having separated them, visit each of them and offer the same deal: If you confess and your accomplice remains silent, he gets the full 10-year sentence and you go free. If you both stay silent, all we can do is give you both 6 months for a minor charge. If you both confess, you each get 5 years.

  Each prisoner individually reasons like this: Either my accomplice confessed or he did not. If he did, and I remain silent, I get 10 years, while if I confess I only get 5. If he remained silent, then by confessing I go free, while by remaining silent I get 6 months. In either case, it is better for me if I confess. Since each of them reasons the same way, both confess, and get 5 years. But although each followed what seemed to be rational argument to achieve the best result, if they had instead both remained silent, they would only have served 6 months."

  By itself, the prisoner's dilemma is not an illusion nor a fallacy, but attempts to resolve it can easily lead you into fallacies and illusions. No general solution is known, although in many special cases it is possible to sketch out an 'optimal strategy.' Read the article referred to above, so that we may have a good and somewhat informed discussion in class. Note that "the Prisoner's Dilemma game is fundamental to certain theories of human cooperation and trust. On the assumption that transactions between two people requiring trust can be modelled by the Prisoner's Dilemma, cooperative behavior in populations may be modelled by a multi-player, iterated, version of the game. It has, consequently, fascinated many, many scholars over the years." [ from Wikipedia ]
  If the prisoner's dilemma makes you dizzy, consider an equally profound, but—at least on the surface, much simpler— dilemma: the Buridan's Ass Dilemma or Paradox (apparently this puzzle was first introduced by Aristotle, and actually Buridan does not even seem to mention it). Here is a formulation by Storrs McCall:

  "Buridan's ass starved to death half-way between two piles of hay because there was nothing to incline his choice towards A rather than B. Here the deliberation reasons for A and B are equally balanced, and as a result no decision is taken. A similar problem, based on fear rather than desire, is the 'railroad dilemma.' What fascinates us in these examples is not just the spectre of decisional paralysis, but the feeling that the outcome—death by indecision—is in a genuine sense an affront to reason. If the ass had been rational, or more rational than he was, he would not have starved. He would have drawn straws and said 'Long left, short right.' Failing this, if he had been clever enough, he could simply have made an arbitrary or criterionless choice. If you believe this is impossible, reflect on how you manage to choose one of a hundred identical tins of tomato soup in a supermarket. The example of the soup tins was a favourite of Macnamara's, who used it with great effect in discussion. If you made the mistake of saying that an arbitrary choice in these circumstances was difficult or impossible, that would indicate that you, like Buridan's ass, were not very intelligent." [ from Deliberation Reasons and Explanation Reasons ]

• One of the areas where cognitive illusions and fallacies play a huge role is statistics and probability theory. Even an elementary introduction to this topic would be impossible within the limits of the present lecture, and I will devote one of the future lectures to it. By way of preparation, here I will only point you to a famous paradox, the so-called Monty Hall Problem. Check also the The Let's Make a Deal Applet, where you can play the game and explore the problem.
  I will also remind you of the 'two jars problem' we discussed in the previous lecture, where probabilities are also involved.

 
Readings, Resources and Questions

• A good, general introduction to perceptual and cognitive illusions is an article by Richard Gregory, Knowledge in Perception and Illusion, which originally appeared in the Phil. Trans. R. Soc. Lond. B, 352, 1121 - 1128 with the kind permission of the Editor
• One of the best articles on cognitive fallacies, especially in physics, is Michael McCloskey, Intuitive Physics, Scientific American, 248, 122-130 (April 1983).
A very readable survey of cognitive illusions and fallacies is Massimo Piattelli Palmarini, Inevitable Illusions: How Mistakes of Reason Rule Our Minds, J Wiley & Sons, NY 1994. The original Italian title is even more interesting; literally translated, it reads: "The Illusion of Knowing: What Hides Behind Our Mistakes."
• A very useful resource is the entry Experimental Science and Mechanics in the Middle Ages, in the The Dictionary of the History of Ideas.
• Given the we are often caught in perceptual and cognitive illusions and fallacies, it is not surprising that philosophers, natural and not, have always tried to find ways to establish and formulate more reliable foundations for knowledge.

  "The fact that the Universe is rational also implies that since our senses can [ be ] deceived then they are unreliable and possible sources of error in our understanding of the workings of Nature. Thus, came the belief that underlying order of the Universe can be understood by pure thought and can be expressed in mathematical form." [ from Mathematics and Science ]

• Since science begins with observations, and since observations are subject to the problems outlined in this lecture, it is not surprising that much attention has been paid to the role of cognition and of its cognitive pitfalls in science. A good starting point is Michael Gorman and Greg Feist's paper on Cognitive Psychology of Science (1994). Here, from this article, is some food for thought:

  "Brewer & Samarapungavan (1991) reviewed the literature on whether children construct theories in a manner similar to scientists; these authors concluded 'that the child can be thought of as a novice scientist, who adopts a rational approach to dealing with the physical world, but lacks the knowledge of the physical world and experimental methodology accumulated by the institution of science' (p. 210). Their point is that the apparent differences in thinking between children and adults is really due to differences in knowledge, not reasoning strategies. For example, they studied second-graders and showed that those who had a flat-earth mental model could incorporate disconfirmatory information consistent with a Copernican view by transforming their model into a hollow sphere. They then used this new mental model to solve a range of problems about the day/night cycle and motion of individuals and objects across the earth' surface."

  "Other researchers have related the beliefs of adults to periods in history of science. (McCloskey, 1983) found that college students held beliefs about physics that resembled those of Philoponus (6th- century) and Buridan (14th-century), who thought that a force was required to set a body in motion, and that the force gradually dissipated. (Clement, 1983) found that freshman engineering students were a little more advanced: protocols of their attempts to solve motion problems resembled Galileo's reasoning in De Motu. These beliefs persist even among advanced physics and engineering students (Clement, 1982). (Pittenger, 1991) calls for more research on how they could be changed, suggesting that the literature has focused too much on textbook science problems and we need to know more about how students view a range of naturalistic phenomena."