 Anova2
Anova2
|
|||||||||
| PREV CLASS NEXT CLASS | FRAMES NO FRAMES | ||||||||
| SUMMARY: NESTED | FIELD | CONSTR | METHOD | DETAIL: FIELD | CONSTR | METHOD | ||||||||
java.lang.ObjectAnova2
public class Anova2
Anova2 - a Java utility to perform an analysis of variance (ANOVA) on a table of data read from a file.
Five experiment designs are supported:
The data must be organized as a matrix with p rows and n columns. p is the number of participants (one per row) and n is the number of within-subjects test conditions (one per column). Each entry in the matrix contains a measurement on the behaviour of interest (e.g., entry speed or accuracy).
For designs with one within-subjects factor, n is the number of levels of the factor. For designs with two within-subjects factors, n is the product of the number of levels of each factor. For example, a two-factor experiment with repeated measures on 15 participants, having 2 levels on the first factor and 3 levels on the second, requires a data file with 15 rows and 2 × 3 = 6 columns. In total, there are 6 test conditions. Such an experiment is called a "2 × 3 within-subjects design".
If two within-subjects factors are used, the nesting of data is important. The columns are ordered with the levels of the second factor nested within the levels of the first factor. As an example, for a 2 × 3 design, the respective order of the data from columns one to six is F1L1-F2L1, F1L1-F2L2, F1L1-F2L3, F1L2-F2L1, F1L2-F2L2, F1L2-F2L3, where F = factor and L = level. The following figure illustrates:
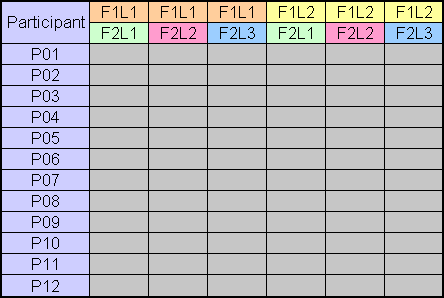
If a between-subjects factor is used, the factor appears as an additional column of nominal data. This is typically a group identifier, and is used, for example, if the participants were divided into groups to counterbalance the order of administering the within-subjects test conditions. A between-subjects factor could also be used for other circumstances (e.g., gender or handedness).
The nominal data entries for the between-subjects factor must appear consecutively for each group. Also, there must be the same number of participants in each group.
Invocation (usage message if invoked without arguments):
java Anova2 file p f1 f2 f3 [-a] [-d] [-m] [-h]
file = data file (comma or whitespace delimited)
p = # of rows (participants) in data file
f1 = # of levels, 1st within-subjects factor ("." if not used)
f2 = # of levels, 2nd within-subjects factor ("." if not used)
f3 = # of levels, between-subjects factor ("." if not used)
-a = output ANOVA table
-d = output debug data
-m = output main effect means
-h = data file includes header lines (see API for details)
(Note: default is no output)
If a between-subjects factor is present, the f3 argument
is an integer
corresponding to the number of groups. f3,
if present, must
divide evenly into p. For example, p = 15, f1
= 3,
and f3 = 3 means the experiment involved 15 participants and a
within-subjects factor with 3 levels. There will be 3 columns of data
for the levels of the f1 factor. Counterbalancing was used with
participants
divided into 3 groups with 5 participants/group. (Here, "group" is
treated like a between-subjects factors.) The groups are identified in the 4th
column.
The following figure illustrates:
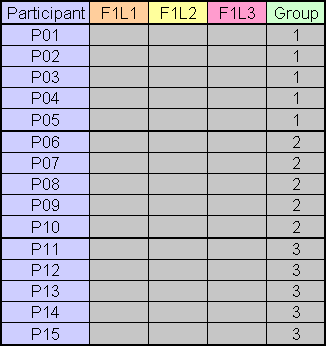
If a between-subjects factor is the only factor (e.g., gender), then the data file contains just two columns, one for the data and one to identify the groups.
If any factor is not present, its command-line argument is replaced with ".".
Four optional arguments are supported:
-a option.
The "-a" option produces the ANOVA table. The default
is no output, so make sure either the -a, -d,
or -m option is present.
-d option.
The "-d" option produces
debug output showing the original
data as well as the means, sums of squares, mean squares, degrees of
freedom, F statistics, and p for the F statistics,
for all effects. Output is produced even for effects that do not exist, so
some values may appear as NaN
or Infinity.
-m option.
The "-m" option outputs the main effect means. This is useful
to ensure that the data are properly extracted from the data matrix in
computing the F statistics for the various main effects and interaction effects.
For example, if the data are improperly nested for two-factor designs,
this error will be apparent by comparing
the output from this option against a manual calculation of the effect means.
-h option.
The "-h" option is used if the data file contains header lines.
In this case, the data file must have four header lines preceding
the data, formatted as follows:
DV: <dependent_variable_name>
F1: <f1_name>, <f1_level_1_name>, <f1_level_2_name>, ...
F2: <f2_name>, <f2_level_1_name>, <f2_level_2_name>, ...
F3: <f3_name>
This option is strictly cosmetic.
The output ANOVA table (-a option)
and main effect means (-m option) will identify
the dependent variable and the names and levels of the factors, as appropriate.
An example for each supported experiment design follows. For
comparison, each analysis is also shown using a commercially available
statistics package called StatView
(currently available as
JMP; http://www.jmp.com/). The named data files are contained in the
zip file with the Anova2 application and API.
ONE-WAY WITH ONE WITHIN-SUBJECTS FACTOR
The file
dix-example-10x2.txt
contains
656,702
259,339
612,658
609,645
1049,1129
1135,1179
542,604
495,551
905,893
715,803
The data are hypothetical and appear in an example in
Dix et al.'s Human-Computer Interaction
(Prentice Hall, 2004, 3rd ed., p. 337). The single factor (F1) is
Icon Design with two levels: Natural and Abstract. The data entries
are the measurements on the dependent variable Task Completion Time (seconds).
The data in the first column are the task completion time
measurements for the Natural icons,
while the data in the second column are the measurements for the
Abstract icons.
Each row contains the measurements taken
on one participant. The hypothetical experiment used 10 participants.The mean task completion times (not shown) are 697.7 s for the Natural icons and 750.3 s for the Abstract icons. An analysis of variance determines if there is a statistically significant difference between these means or if the difference is likely due to chance. The analysis is performed using
java Anova2 dix-example-10x2.txt 10 2 . . -a
and produces the following output on the console:
======================================================================
Effect df SS MS F p
----------------------------------------------------------------------
Participant 9 1231492.000 136832.444
F1 1 13833.800 13833.800 33.359 3.0E-4
F1 x Par 9 3732.200 414.689
======================================================================
As seen in the table, and as might appear in a research paper,
"The experiment revealed a significant effect of Icon Type on
Task Completion Time (F1,9 = 33.36, p < .0005)."
Even though p = 3.0E-4 = .0003 in the ANOVA table,
it is typically reported in research papers as p < n, where
n is the closest more conservative value from the set
.05, .01, .005, .001, .0005, .0001. Note also that in North American
publications, the zero preceding the decimal point is typically omitted (because
p is constrained between 0 and 1).
Two other outcomes are worth noting, where the results are non-significant. If p is above .05 and F > 1, p is reported as "p > .05". This means there is a greater than 5% chance that the differences in the means is due to chance. This is sufficient lack of confidence to deem the difference in the means "not significant". If p is above .05 and F ≤ 1, then p is not reported at all, but is replaced with "ns" meaning "not significant". This format is used is because it is impossible for differences in the means to be significant where F ≤ 1.
The results above are shown below in an ANOVA on the same data using StatView.

Lambda and Power are not calculated in Anova2.
Lambda is a measure of
the noncentrality of the F distribution,
calculated as F × N, where
N is the degrees of freedom of
the effect. Power, which ranges from 0 to 1,
is the ability to detect an effect, if there is one.
The closer to one, the more the experiment is likely
to find an effect, if one exists in the population.
Power > .80 is generally considered
acceptable; i.e., if p is significant
and Power > .80, then it is likely that
the effect found actually exists.
TWO-WAY WITH ONE WITHIN-SUBJECTS FACTOR AND ONE BETWEEN SUBJECTS FACTOR
The hypothetical experiment described by Dix et al. was
a within-subjects design and would likely use counterbalancing to cancel the
learning effects that might occur as participants advanced from the
first test condition to the second. With two conditions, the
participants are divided into two groups of equal size.
Half the participants
would be tested on the Natural icons first followed by the Abstract icons, while
the other half would be tested in the reverse order. Like this, "Group"
is a between-subjects factor with five participants in each group.
To include this in the analysis,
we append a column to the data file, creating a new data file
called
dix-example-h10x2b.txt.
The new column identifies
the groups as either "NA" (Natural first, Abstract second) or "AN"
(Abstract first, Natural second). The file is also modified to
include header lines, as per the requirements of the -h
option. Here are the data:
DV: Completion Time (s)
F1: Icon Type, Natural, Abstract
F2: .
F3: Group
656,702,NA
259,339,NA
612,658,NA
609,645,NA
1049,1129,NA
1135,1179,AN
542,604,AN
495,551,AN
905,893,AN
715,803,AN
Note that the data for each group are in consecutive rows: 5 rows for the
NA group, followed by 5 rows for the AN group. THIS IS IMPORTANT!
To analyse these data, we replace "." with "2" for f3,
indicating the presence of a between-subjects factor with 2 groups.
The -h option is also needed:
java Anova2 dix-example-h10x2b.txt 10 2 . 2 -h -a
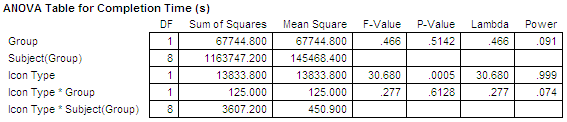
ANOVA table for Completion Time (s)
==========================================================================
Effect df SS MS F p
--------------------------------------------------------------------------
Group 1 67744.800 67744.800 0.466 0.5142
Participant(Group) 8 1163747.200 145468.400
Icon Type 1 13833.800 13833.800 30.680 4.0E-4
Icon Type x Group 1 125.000 125.000 0.277 0.6128
Icon Type x P(Grou 8 3607.200 450.900
==========================================================================
The Group effect was not statisticaly significant
(F1,8 = 0.466, ns).
This is good news, since it means counterbalancing
worked; i.e., any learning effect that might have occurred for the AN group
was effectively offset by a similar and opposing
learning effect for the NA group.
The Icon Type (F1) × Group interaction effect also failed to achieve statistical
significance (F1,8 = 0.277, ns). This means there
was no asymmetrical transfer of skill, also good news.
Asymmetric transfer of skill means some aspect of one condition
helped (or hindered!) the other condition,
without a corresponding reverse effect.The same analysis in StatView appears as
TWO-WAY WITH TWO WITHIN-SUBJECTS FACTORS
For the next example, we use data from an experiment on "eye typing" -- the use of eye tracking technology for text entry using an on-screen soft keyboard. The experimental methodology and data analyses are described in "Audio and visual feedback during eye typing " (Majaranta, MacKenzie, Aula, & Räihä, CHI 2003). The experiment was a 4 × 4 repeated-measures design with 13 participants. The factors and levels were as follows:

There was no counterbalancing as the order of presenting the feedback modes was randomized.
Although there were several dependent variables, only error rate (%) is
presented here. The error rate ANOVA table is in
errorrate-h13x16.txt:
(abbreviated to fit page)
DV: Error Rate (%)
F1: Feedback, Speech Only, Click+Visual, Speech+Visual, Visual Only
F2: Block, B1, B2, B3, B4
F3: .
0.0,0.0,0.0,0.0,0.0,0.7142857142000001,0.0,0.0,0.0,0.0,0.0,0.0, ...
0.0,0.0,0.0,0.0,1.7391304347999998,0.0,0.0,0.0,0.0,0.909090909, ...
0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,4.4999282534,3.636363636,0.0,0.0, ...
0.0,0.0,0.0,0.0,1.9047619048000002,0.0,0.0,1.8253968254,0.0, ...
0.0,0.0,0.0,0.0,1.1111111112,1.1111111112,0.0,0.0,0.0,0.0,0.0, ...
0.0,0.0,0.0,0.0,1.052631579,0.0,0.0,2.222222222,0.0,0.0, ...
0.909090909,0.0,0.0,0.0,0.7407407408,1.7391304347999998, ...
0.0,0.0,0.0,0.0,0.909090909,0.0,0.0,0.0,0.0,0.0,0.0, ...
0.0,0.0,0.0,0.8695652173999999,1.4814814814,0.0,0.0,0.0, ...
0.0,0.0,0.0,0.0,0.7407407408,0.0,0.0,1.8461538462,1.052631579, ...
0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.0,0.7407407408,0.0,0.0, ...
1.6103059582,0.0,0.0,0.0,2.0,0.0,1.052631579,0.7407407408,0.0, ...
4.350649350199999,0.0,1.052631579,0.0,1.3793103448,3.052631579, ...
The data entries are full precision, so the table above is unsightly. The four header lines were
manually inserted to improve the output generated by Anova2.
The -m option may be used prior to the analysis, to view
the overall effect means:
java Anova2 errorrate-h13x16.txt 13 4 4 . -h -m
=============================
----- MAIN EFFECT MEANS -----
=============================
Grand mean: 0.5510756505634619
Participant means:
p1=0.0446
p2=0.4523
p3=0.7625
p4=0.9495
p5=0.2850
p6=0.5117
p7=0.5671
p8=0.2340
p9=0.2213
p10=0.4305
p11=0.1620
p12=0.6440
p13=1.8994
Feedback means:
Speech Only=0.1691
Click+Visual=0.5831
Speech+Visual=0.5002
Visual Only=0.9520
Block means:
B1=1.05367
B2=0.44541
B3=0.36877
B4=0.33646
Use of the -m option is highly recommended in situations were more than one factor is present. The means for the levels
of the factors should be compared against the same values computed manually or in a spreadsheet to ensure the nesting of data is correct.
The analysis of variance is performed as follows:
java Anova2 errorrate-h13x16.txt 13 4 4 . -h -a
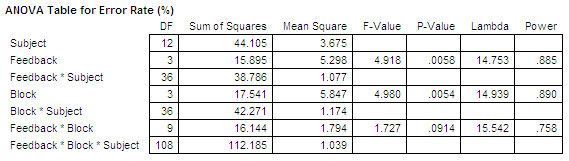
ANOVA_table_for_Error Rate (%)
===========================================================================
Effect df SS MS F p
---------------------------------------------------------------------------
Participant 12 44.105 3.675
Feedback 3 15.895 5.298 4.918 0.00577
Feedback_x_Par 36 38.786 1.077
Block 3 17.541 5.847 4.980 0.00543
Block_x_Par 36 42.271 1.174
Feedback_x_Block 9 16.144 1.794 1.727 0.09143
Feedback_x_Block_x_Par 108 112.185 1.039
===========================================================================
As seen in the table, the main effect of Feedback Mode
on Error Rate was
significant (F3,36 = 4.92, p < .01).
There was also a significant improvement in entry speed
with practice as evident
by the significant effect of Block
(F3,36 = 4.98, p < .001).
However, the Feedback Mode × Block interaction effect
was not significant
(F9,108 = 1.73, p > .05).
The same data similarly analysed in StatView yield the following ANOVA table:
THREE-WAY WITH TWO WITHIN-SUBJECTS FACTORS AND ONE BETWEEN-SUBJECTS FACTOR
The file
softkeyboard-h12x10b.txt
contains the data from
an experiment comparing two layouts of soft keyboards.
The experiment used 12 participants in a 2 × 5 repeated-measures design.
The participants
tapped the phrase "the quick brown fox jumps over the lazy dog" five times
on each of two soft keyboard layouts. Each entry of a phrase is called
a "trial". The dependent variable was
Entry Speed in words per minute. There were two independent variables,
or factors:

Testing was counterbalanced: Each participant entered the phrase five times with one layout, then five times with the other layout. Half the participants used Opti first, following by Qwerty. The other half used the layouts in the reverse order. Thus, Group was a between-subjects factor with two levels, Group A and Group B.
The data file was edited to show the variable names in header lines and the participant group as the last entry on each data line: (abbreviated to fit page)
DV: Entry Speed (wpm)
F1: Layout, Opti, Qwerty
F2: Trial, T1, T2, T3, T4, T5
F3: Group
7.589351375,12.37706884, ... 31.34872418,31.55963303,33.81389253,A
9.32417781,12.900000000, ... 28.89137738,29.94776553,35.0305499,A
9.207708779,9.504512802, ... 24.14599906,27.95232936,28.10457516,A
7.158712542,7.754733995, ... 25.0242483,20.65652522,24.80769231,A
9.532606688,13.18007663, ... 28.58725762,30.75089392,30.55062167,A
9.290601368,11.66628985, ... 26.9733403,24.71264368,28.74651811,A
9.417776967,9.194583036, ... 27.21518987,28.04347826,28.32052689,B
5.347150259,7.188631931, ... 20.31496063,19.28971963,20.39525692,B
14.1797197,15.10980966, ... 30.71428571,31.67587477,34.01450231,B
8.970792768,10.39693734, ... 27.68240343,25.51928783,25.12171373,B
9.552017771,12.69372694, ... 30.97238896,32.33082707,33.7254902,B
8.510638298,12.11267606, ... 33.07692308,32.84532145,32.04968944,B
The main effect means are computed as follows:
java Anova2 softkeyboard-h12x10b.txt 12 2 5 2 -h -m
=============================
----- MAIN EFFECT MEANS -----
=============================
Grand mean: 19.37750420382501
Participant means:
p1=20.7983
p2=21.5246
p3=18.4274
p4=15.5269
p5=20.6872
p6=18.2638
p7=19.6175
p8=12.7009
p9=23.1342
p10=18.1388
p11=22.4065
p12=21.3041
Layout means:
Opti=12.2699
Qwerty=26.4852
Trial means:
T1=15.4229
T2=18.1753
T3=20.2560
T4=20.9482
T5=22.0851
Group means:
A=19.2047
B=19.5503
Entry speed in words per minute was much faster
with the Qwerty layout (26.5 wpm) than with the Opti layout (12.3 wpm).
Let's see if the variances
were sufficiently low to deem the difference in the means
statistically significant:
java Anova2 softkeyboard-h12x10b.txt 12 2 5 2 -h -a
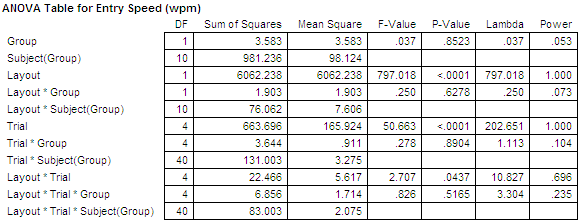
ANOVA table for Entry Speed (wpm)
==========================================================================
Effect df SS MS F p
--------------------------------------------------------------------------
Group 1 3.583 3.583 0.037 0.8523
Participant(Group) 10 981.236 98.124
Layout 1 6062.238 6062.238 797.018 0.0000
Layout x Group 1 1.903 1.903 0.250 0.6278
Layout x P(Group) 10 76.062 7.606
Trial 4 663.696 165.924 50.663 0.0000
Trial x Group 4 3.644 0.911 0.278 0.8904
Trial x P(Group) 40 131.003 3.275
Layout x Trial 4 22.466 5.617 2.707 0.0437
Layout x Trial x Group 4 6.856 1.714 0.826 0.5165
Layout x Trial x P(Gro 40 83.003 2.075
==========================================================================
Yes. The F statistic, which is the ratio of the mean squares (6062.238 /
7.606 = 797.0) is extremely high. Not
surprisingly, the F statistic for the main effect of Layout on Entry Speed
is highly significant (F1,10 = 797.0, p < .0001).
In all, the table shows three main effects and four interaction effects.
There is
considerable leeway in presenting the results in a research paper. See
Experiment 1 in
"Using paper mockups for
evaluating soft keyboard layouts" (MacKenzie & Read, CASCON 2007) for an example of how the results
above might be reported.The results above are confirmed using StatView:
ONE-WAY WITH ONE BETWEEN-SUBJECTS FACTOR
A one-way between-subjects design might be used, for example, to
test whether an interface or interaction technique works better
with left-handed vs. right-handed users (or with males vs. females).
In this case, the design must be between-subjects because a participant
cannot be both left-handed and right-handed (or male and female!).
Two groups of participants are required. Let's consider the case
where five left-handed users (L) and five right-handed users (R) are
measured on a task. The independent variable is Handedness with
two levels, Left and Right, and the dependent variable
is Time (seconds) to complete a task. Here are the example data, stored
in
anova-h10b.txt:
DV: Time (s)
F1: .
F2: .
F3: Handedness
25.6,L
23.4,L
19.4,L
28.1,L
25.9,L
14.3,R
22.0,R
30.4,R
21.1,R
19.3,R
The means (not shown)
for the Left- and Right-handed groups were 28.48 s and 21.42 s,
respectively. So, the Left-handed group took,
on average, 33% longer to complete the task.
That's a huge performance difference,
but is the difference in the means statistically significant? Let's see.
The analysis is performed as follows:
java Anova2 anova-h10b.txt 10 . . 2 -h -a
ANOVA table for Time (s)
==========================================================================
Effect df SS MS F p
--------------------------------------------------------------------------
Handedness 1 23.409 23.409 1.043 0.3371
Residual 8 179.616 22.452
==========================================================================
Despite the observation that the Left-handed group took considerable
longer to complete the task, the difference between
the groups
was not statistically significant
(F1,8 = 1.04, p > .05). This might be partly
attributed to the small number of participants tested. It might also
be attributed simply to a lack of bias in the interface for
Left-handed vs. Right-handed users.Using StatView, the above results are confirmed:
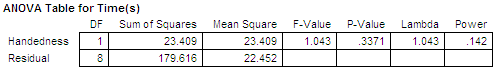
Features to come
A few features are planned for this program.
One is to allow the names and levels
of the independent variables,
and the names and units for the dependent variables to be specified
in the data file, and, hence, to appear in the output analysis.
Another
is to perform post hoc comparisons to determine which means
are significantly different from each other, in the event the
F statistic is significant.
A note on the calculations:
The trickiest part is the calculation of p, representing
the significance of F.
This comes by way of the method FProbability in the
Statistics class in the University of Waikato's
weka.core package. This package was obtained from
Statistics.class copyright notice:
-----
Class implementing some distributions, tests, etc. The code is mostly adapted from the
CERN Jet Java libraries: Copyright 2001 University of Waikato Copyright 1999 CERN - European
Organization for Nuclear Research. Permission to use, copy, modify, distribute and sell
this software and its documentation for any purpose is hereby granted without fee, provided
that the above copyright notice appear in all copies and that both that copyright notice and
this permission notice appear in supporting documentation. CERN and the University of Waikato
make no representations about the suitability of this software for any purpose. It is provided
"as is" without expressed or implied warranty.
-----
| Constructor Summary | |
|---|---|
Anova2()
|
|
| Method Summary | |
|---|---|
static void |
main(java.lang.String[] args)
|
| Methods inherited from class java.lang.Object |
|---|
equals, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait |
| Constructor Detail |
|---|
public Anova2()
| Method Detail |
|---|
public static void main(java.lang.String[] args)
throws java.io.IOException
java.io.IOException
|
|||||||||
| PREV CLASS NEXT CLASS | FRAMES NO FRAMES | ||||||||
| SUMMARY: NESTED | FIELD | CONSTR | METHOD | DETAIL: FIELD | CONSTR | METHOD | ||||||||