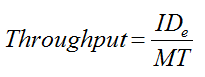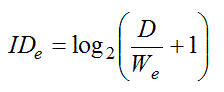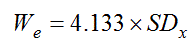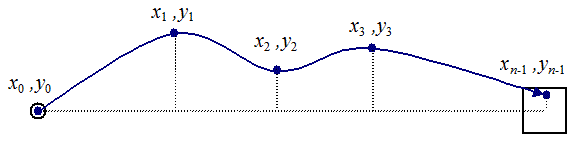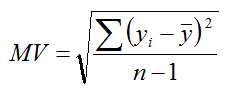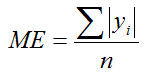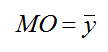MacKenzie, I. S., Kauppinen, T., & Silfverberg, M. (2001). Accuracy measures for evaluating computer pointing devices. Proceedings of the ACM Conference on Human Factors in Computing Systems - CHI 2001, pp. 9-16. New York: ACM. [software]

Accuracy Measures for
Evaluating Computer Pointing Devices

I. Scott MacKenzie1, Tatu Kauppinen2, & Miika Silfverberg2

1Department of Computer Science
York University
Toronto, Ontario, Canada M3J 1P3
smackenzie@acm.org

2Nokia Research Center
P.O. Box 407
FIN-00045 Nokia Group, Finland
tatu.kauppinen@nokia.com, miika.silfverberg@nokia.com

Abstract
In view of the difficulties in evaluating computer pointing devices across different tasks within dynamic and complex systems, new performance measures are needed. This paper proposes seven new accuracy measures to elicit (sometimes subtle) differences among devices in precision pointing tasks. The measures are target re-entry, task axis crossing, movement direction change, orthogonal direction change, movement variability, movement error, and movement offset. Unlike movement time, error rate, and throughput, which are based on a single measurement per trial, the new measures capture aspects of movement behaviour during a trial. The theoretical basis and computational techniques for the measures are described, with examples given. An evaluation with four pointing devices was conducted to validate the measures. A causal relationship to pointing device efficiency (viz. throughput) was found, as was an ability to discriminate among devices in situations where differences did not otherwise appear. Implications for pointing device research are discussed.

Keywords: Computer pointing devices, performance evaluation, performance measurement, cursor positioning tasks

INTRODUCTION

The popularization of the graphical user interface (GUI) began in 1984 with the Apple Macintosh. Since then, GUIs have evolved and matured. A key feature of a GUI is a pointing device and "point-and-click" interaction. Today, pointing devices are routinely used by millions of computer users.

The pointing device most common in desktop systems is the mouse, although others are also available, such as trackballs, joysticks, and touchpads. Mouse research dates to the 1960s with the earliest publication from English, Engelbart, and Berman [6]. The publication in 1978 by Card and colleagues at Xerox PARC [4] was the first comparative study. They established for the first time the benefits of a mouse over a joystick. Many studies have surfaced since, consistently showing the merits of the mouse over alternative devices (e.g., [7, 9, 13]). This paper focuses on the evaluation of computer pointing devices in precision cursor positioning tasks. The primary contribution is in defining new quantitative measures for accuracy that can assist in the evaluations.

PERFORMANCE EVALUATION

The evaluation of a pointing device is tricky at best, since it involves human subjects. There are differences between classes of devices (e.g., mouse vs. trackball) as well as differences within classes of devices (e.g., finger controlled trackball vs. thumb-controlled trackball). Generally, between-class differences are more dramatic, and hence more easily detected through empirical evaluations.

The most common evaluation measures are speed and accuracy. Speed is usually reported in its reciprocal form, movement time (MT ). Accuracy is usually reported as an error rate - the percentage of selections with the pointer outside the target. These measures are typically analysed over a variety of task or device conditions.

An ISO standard now exists to assist in evaluating pointing devices. The full standard is ISO 9241, "Ergonomic design for office work with visual display terminals (VDTs)". Part 9 is "Requirements for non-keyboard input devices" [8]. ISO 9241-9 proposes just one performance measurement: throughput. Throughput, in bits per second, is a composite measure derived from both the speed and accuracy in responses. Specifically,

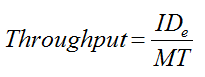
  (1)

where

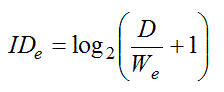
  (2)

The term IDe is the effective index of difficulty, in "bits". It is calculated from D, the distance to the target, and We , the effective width of the target. The use of the "effective" width (We ) is important. We is the width of the distribution of selection coordinates computed over a sequence of trials, calculated as

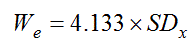
  (3)

where SDx is the standard deviation in the selection coordinates measured along the axis of approach to the target. This implies that We reflects the spatial variability (viz. accuracy) in the sequence of trials. And so, throughput captures both the speed and accuracy of user performance. See [5, 10] for detailed discussions.

NEW ACCURACY MEASURES

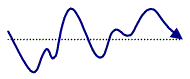
Besides discrete errors or spatial variability in selection coordinates, there are other possibilities for accuracy and each provides information on aspects of the interaction. In a "perfect" target selection task, the user moves the pointer by manipulating the pointing device; the pointer proceeds directly to the centre of the target and a device button is pressed to select the target (see Figure 1).


Figure 1. A "perfect" target-selection task

In practice, this behaviour is rare. Many variations exist and all occur by degree, depending on the device, the task, and other factors. In this section, we identify some of these behaviours and formulate quantitative measures to capture them.

We are not suggesting that it is wrong to report error rates. Rather, our goal is to augment this with more expressive measures of accuracy - measures that can assist in characterizing possible control problems that arise with pointing devices.

Movement Variability

Devices like mice, trackballs, joysticks, and touchpads have a variety of strengths and weaknesses, and these are well documented in past studies [4, 5, 7, 9, 11]. However, analyses tend to focus on gross measures such as movement time and error rates. These measures adequately establish "that there is a difference", but their power in eliciting "why there is a difference" is limited. Establishing "why" is more likely borne out in more thorough analyses, for example, in considering movement path.

Consider the trackball's means to effect pointer motion. To move the pointer a long distance, users may "throw" the ball with a quick flick of the index finger, whereas more precise pointer movement is effected by "walking" the fingers across the top of the ball. These behaviours, which are not possible with other pointing devices, may affect the pointer's path. Such effects may not surface if analyses are limited to movement time or error rates.

Dragging tasks are particularly challenging for trackballs. This has been attributed to an interaction between the muscle groups to effect pointer motion (index finger) vs. those to press a button (thumb) [11]. In the study cited, however, only movement times and error rates were measured. Since these are gross measures (one per trial), their power in explaining behaviour within a trial is limited. Here we see a clear need for more detailed measures that capture characteristics of the pointer's path.

Several measures are possible to quantify the smoothness (or lack thereof) in pointer movement, however analyses on the path of movement are rare in published studies. (For exceptions, see [1, 12].) One reason is that the computation is labour-intensive. The pointer path must be captured as a series of sample points and stored in a data file for subsequent analysis. Clearly, both substantial data and substantial follow-up analyses are required.

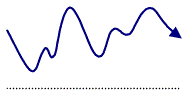
An example of a task where the path of the pointer is important is shown in Figure 2. When selecting items in a hierarchical pull-down menu, the pointer's path is important. If the path deviates too far from the ideal, a loss of focus occurs and the wrong menu item is temporarily active. Such behaviour is undesirable and may impact user performance.


Figure 2. The importance of pointer path

Several measures are now proposed to assist in identifying problems (or strengths) for pointing devices in controlling a pointer's movement path. Figure 3 shows several path variations. Note that the pointer start- and end-point are the same in each example. Clearly, accuracy analyses based only on end-point variation cannot capture these movement variations.

We begin by proposing several simple measures that require only that certain salient events are logged, tallied, and reported as a mean or ratio.

Target Re-entry (TRE ). If the pointer enters the target region, leaves, then re-enters the target region, then target re-entry (TRE ) occurs. If this behaviour is recorded twice in a sequence of ten trials, TRE is reported as 0.2 per trial. A task with one target re-entry is shown in Figure 3a.


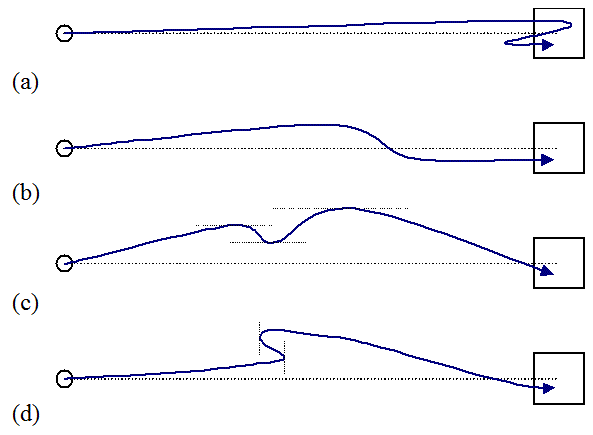
Figure 3. Path variations. (a) target re-entry (b) task axis crossing
(c) movement direction change (d) orthogonal direction change

An example where target re-entry was not used, yet may have helped, is Akamatsu et al.'s evaluation of a mouse with tactile feedback [2]. This study found a main effect on fine positioning time - the time to select the target after the pointer entered the target region. With tactile feedback, users exhibited a lower fine positioning time than under the no feedback, auditory feedback, and colour feedback conditions. A measure such as target re-entry may also serve to reveal differences among on-target feedback conditions, for example.

Other counts of path accuracy events are possible, and may be relevant, depending on the device or task.

Task Axis Crossing (TAC ). In Figure 3b, the pointer crosses the task axis on the way to the target. In the example, the ideal path is crossed once, so one task axis crossing (TAC ) is logged. This measure could be reported either as a mean per trial or a mean per cm of pointer movement.

TAC may be valuable if, for example, the task is to trace along a pre-defined path as closely as possible.

Movement Direction Change (MDC ). In Figure 3c, the pointer's path relative to the task axis changes direction three times. Each change is logged as a movement direction change (MDC ).

MDC and TAC are clearly correlated. One or the other may be of interest, depending on the task or device.

Orthogonal Direction Change (ODC ). In Figure 3d, two direction changes occur along the axis orthogonal to the task axis. Each change is logged as one orthogonal direction change (ODC ). If this measure is substantial (measured over repeated trials), it may signal a control problem in the pointing device.

The four measures above characterize the pointer path by logging discrete events. Three continuous measures are now proposed: movement variability, movement error, and movement offset.

Movement Variability (MV ). Movement variability (MV ) is a continuous measure computed from the x-y coordinates of the pointer during a movement task. It represents the extent to which the sample points lie in a straight line along an axis parallel to the task axis.

Consider Figure 4, which shows a simple left-to-right target selection task, and the path of the pointer with five sample points.


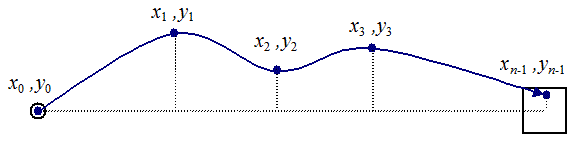
Figure 4. Sample coordinates of pointer motion

Assuming the task axis is y = 0, yi is the distance from a sample point to the task axis, and y[overbar] is the mean distance of the sample points to the task axis. Movement variability is computed as the standard deviation in the distances of the sample points from the mean:

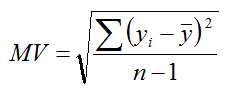
  (4)

For a perfectly executed trial, MV = 0.

Movement Error (ME ). Movement error (ME ) is the average deviation of the sample points from the task axis, irrespective of whether the points are above or below the axis. Assuming the task axis is y = 0 in Figure 4, then

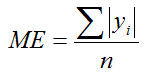
  (5)

For an ideal task, ME = 0. As with MDC and TAC, ME and MV are likely correlated. One or the other may bear particular merit depending on the movement characteristics of the device.

Movement Offset (MO ). Movement offset (MO ) is the mean deviation of sample points from the task axis. Assuming the task axis is y = 0 in Figure 4, then

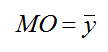
  (6)

Movement offset represents the tendency of the pointer to veer "left" or "right" of the task axis during a movement.

For an ideal task, MO = 0. Several movement responses, and the relative values of movement variability, error, and offset are shown in Figure 5.

  Movement Responses
Movement
Variability 		Low Low High High
Movement
Error 		Low Very High High Very High
Movement
Offset 		Low High Low High
Figure 5. Comparison of movement variability, movement error, and movement offset

METHOD

To test our accuracy measures, we designed an experiment with standard pointing devices.

Participants

Twelve paid participants (9 male, 3 female) were recruited, based on a posting at a local university. All participants were regular users of a GUI and mouse. Two participants were regular trackball users and one a regular joystick user. None were regular touchpad users.

Apparatus

The experiment was conducted on a Pentium-class desktop PC running Windows 98. The experimental software was developed in Visual Basic (version 6). Output was presented on a 17" monitor. Input was via the following four stand-alone pointing devices:

Procedure

Participants were randomly assigned to one of four groups (3 participants/group). Each participant was tested with all devices. The order of devices differed for each group according to a balanced Latin square.

Prior to testing, participants were briefed on the purpose of the experiment. The task was demonstrated and a sequence of warm-up trials was given prior to testing. The task was the simple multidirectional point-select task in ISO 9241-9 [8] (see Figure 6).


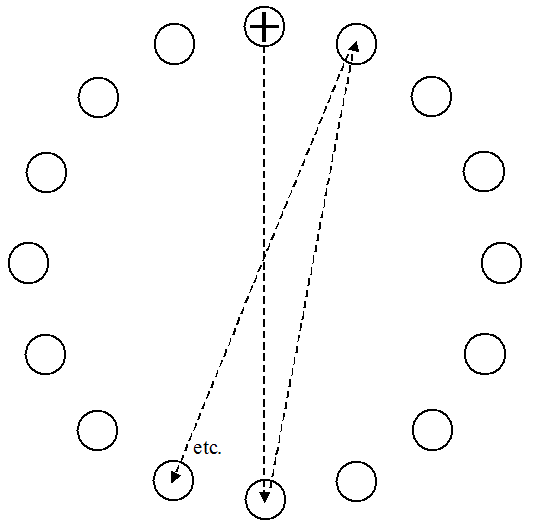
Figure 6. Experiment task showing a sequence of 15 target selections (see text for details)

There were 16 circular targets arranged in a circular layout. The diameter of the layout circle and targets was 400 pixels (180 mm) and 30 pixels (13 mm), respectively. Since our goal was to test our accuracy measures across several pointing devices, we used only one task condition with a nominal difficulty of 3.8 bits.

A sequence of trials began when a participant clicked in the top target in the layout circle. The next selection was the target on the opposite side of the layout circle, and so on. The first three selections are identified by the dotted lines in Figure 6. At all times, the "next" target was identified with a purple crosshair, which moved from target to target as a sequence progressed.

Participants were instructed to select the targets as quickly and accurately as possible, while not exceeding approximately one error per sequence. A beep was heard for any selection with the pointer outside the target.

The experiment proceeded by "sequences" and "blocks". A sequence was 15 target selections (see Figure 6). (Note: Data collection began with the first selection, thus data were not collected for the top target.) A block had 5 sequences. Ten blocks, lasting about one hour total, were given for each device. Data collection was continuous within a sequence; however, rests were allowed between sequences.

Design

The experiment was a 4 × 5 × 10 within-subjects factorial design. The factors and levels were as follows:

With 12 participants and 15 selections per sequence, the total number of trials in the experiment was

       12 × 15 × 4 × 5 × 10 = 36,000

Samples were collected at a rate of 40 per second. Since our measures necessitated recording the pointer path, a large amount of data was collected (approximately 40 MB). Analyses are given in the following section.

RESULTS AND DISCUSSION

We begin by analysing the main effects and interactions on the traditional measures of movement time, throughput, and error rate.

Movement Time and the Learning Effect

All participants were regular mouse users; however, some had little or no experience with other devices. In addition, participants had to gain familiarity with the task. For these reasons, a learning effect was expected, perhaps confounded with previous experience with the mouse.

Figure 7 shows the effects of learning (i.e., block) and device on movement time. Clearly, the mouse was the fastest device, the joystick the slowest. The mouse also had the flattest learning curve, as indicative of users' prior experience. The main effects were significant for device (F3,396 = 63.9, p < .001) and block (F9,396 = 43.6, p < .001). Not surprisingly, the device by block interaction was also significant (F27,396 = 2.28, p < .001).


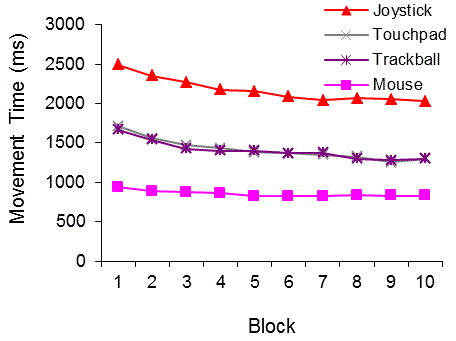
Figure 7. Movement time by device and block

Helmhert contrasts showed that the block effect was not significant after block five. Therefore, subsequent analyses are based on means from blocks six to ten only.

Throughput and Error Rates

Figure 8 shows throughput and error rate by device, with 95% confidence intervals. As seen, the variance is substantially larger for error rate than for throughput. This is expected as error rates are generally more variable than movement time [3] or throughput. The lower variance for throughput is also expected since the calculation inherently trades speed with accuracy (see Equations 1-3).

The throughput was 4.9 bps for the mouse, 3.0 bps for the trackball, 1.8 bps for the joystick, and 2.9 bps for the touchpad. The main effect for device was clearly significant (F3,44 = 108.4, p < .001). Paired t-tests revealed significant differences in throughput across all device combinations except between the trackball and touchpad. Concluding that these two devices performed about the same is premature, however. As shown later, the additional discriminatory power of the new accuracy measures revealed a difference between the trackball and touchpad that did not appear in throughput measures.

The throughputs for the mouse and trackball are within 10% of those reported previously (e.g., [11]). It is notable that contrary to Douglas et al. [5], the joystick had a lower throughput than the touchpad. This may be attributed to the different products tested. We used an Interlink DeskStick, a stand-alone joystick based on force-sensing resistive (FSR) technology, whereas Douglas et al. used an IBM TrackPoint, a joystick based on strain gauge technology built in to the keyboard of an IBM ThinkPad notebook.


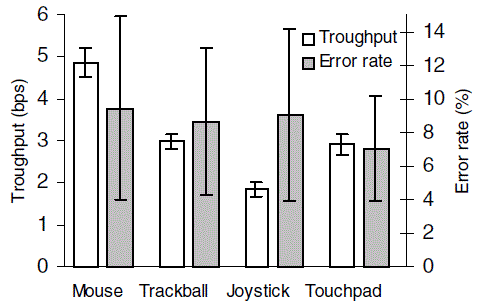
Figure 8. Throughput and error rate by device with 95% confidence intervals

Error rates were 9.4% for the mouse, 8.6% for the trackball, 9.0% for the joystick, and 7.0% for the touchpad. The differences were not statistically significant (F3,44 = 0.197, p < .05).

New Accuracy Measures (and Their Relationship to Throughput)

Table 1 shows the means and standard deviations of the seven accuracy measures across the four devices. Recall that for all measures, lower scores are better. The units in Table 1 are "mean count per trial" for TRE, TAC, MDC, and ODC; and "pixels" for MV, ME, and MO, where 1 pixel = 0.43 mm as measured on the display. One-way ANOVAs showed significant differences between the devices across all accuracy measures. (Absolute values were used for MO, since both negative and positive values are possible; see Equation 6.) We begin by examining the relationship between these measures and throughput.

Table 1
Means and Standard Deviations of Accuracy Measures for Each Device
Variable Mouse Trackball Joystick Touchpad F
mean sd mean sd mean sd mean sd
Target re-entry (TRE ) 0.07 0.04 0.26 0.13 0.33 0.08 0.15 0.04 27.92***
Task axis crossing (TAC ) 1.7 0.2 2.2 0.4 2.0 0.3 1.64 0.19 9.83***
Movement direction change (MDC ) 3.6 1.0 5.7 1.6 6.1 3.8 3.6 0.7 4.74**
Orthogonal direction change (ODC ) 0.8 0.4 1.8 0.6 1.5 0.9 0.8 0.2 8.59***
Movement variability (MV ) 10.5 3.9 15.9 2.5 17.6 3.8 11.7 2.4 13.54***
Movement error (ME ) 11.6 4.7 16.5 3.6 18.7 3.5 13.2 2.5 9.09***
Movement offset (MO ) 2.5 1.0 3.4 0.8 5.1 1.8 3.9 2.4 5.42***
***p < .001, **p < .01

The major aim of pointing device research is to develop devices that are as efficient as possible. Throughput is an accepted measure - now endorsed in an ISO standard - with a long history in pointing device research. It is derived from speed and accuracy, represented by movement time and end-point selection coordinates, respectively. These are gross measures (one per trial) lacking any information on movement during a trial. For that reason, it is important to develop additional accuracy measures with the potential to explain why some pointing devices are more efficient than others.

In this section, we illustrate how the new accuracy measures can explain differences borne out in the throughput measurements. That is, if all or some of the candidate accuracy measures have a causal relationship to throughput, this is useful in the development and evaluation of pointing devices because there are more ways to determine why such differences exist and to adjust a design accordingly.

Table 2
Adjusted Partial Correlations Between Accuracy Measures
  1. 2. 3. 4. 5. 6. 7. 8.
1. Throughput                
2. Target re-entry (TRE ) -.82***              
3. Task axis crossing (TAC ) -.56*** -.62***            
4. Movement direction change (MDC ) -.40*** -.36* -.64***          
5. Orthogonal direction change (ODC ) -.50*** -.66*** -.63*** -.75***        
6. Movement variability (MV ) -.69*** -.66*** -.31* -.49*** -.71***      
7. Movement error (ME ) -.60*** -.54*** -.16 -.46*** -.66*** -.97***    
8. Movement offset (MO ) -.73*** -.36*** -.04 -.06 -.25 -.54*** -.55***  
***p < .001; *p < .05

To determine if the new accuracy measures have a causal relationship to throughput, we first calculated the participant and device adjusted partial correlations between throughput and all seven accuracy measures. These are shown in Table 2. The correlations clearly show that all seven accuracy measures are inversely related to throughput. Correlations range from -.40 to -.82. This is expected: it simply means that low throughput is coincident with inaccurate movement as measured with TRE, TAC, MDC, ODC, MV, ME, and MO.

It is noteworthy, however, that some of the inter-correlations in Table 2 are high. This is especially true for MV and ME, which have about 94% of their variance in common (r = .97, r 2 = .94). For this reason, some of the measures may capture more-or-less the same behaviour, as noted earlier for TAC and MDC. This was examined with a multiple regression analysis using forward selection, whereby predictors are entered in order of the magnitude of their independent contribution to the dependent variable. See, for example, [14] for details.

The result was that only two of the measures made a significant contribution to the prediction of throughput. These measures - TRE and MO - explained about 61% of variance in throughput. TRE explained about 41%, and MO about 19%. This final model was clearly significant (F2,45 = 40.74, p < .001).

Although TRE and MO were the only measures contributing significantly to the prediction of throughput, this does not mean the other measures are without merit. Consider TRE as an example. A large number of target re-entries does not directly imply what is wrong with the pointing device. However, if we know, for example, that another measure has a causal effect on TRE (Table 2), this may provide insight on how to reduce TRE. We tested this again using multiple regression but with TRE as the dependent variable. Of the remaining six measures, orthogonal direction change (ODC ) had a high influence on TRE, explaining 49% of the variance.

Examining and correcting the underlying source of poor accuracy measures should help improve pointing device throughput. Caution is warranted, however, in advancing any claim that some of the measures are more important than others. The experiment described here is the first to test the new measures. Although TRE, MO, and ODC had a significant negative effect on throughput in this study, in other contexts, such as different devices and/or tasks, the relative contribution of the measures in explaining throughput may be entirely different.

Discriminating Among Devices

The relationship between our seven accuracy measures and throughput has been studied thus far treating the four devices as a single group. This is a reasonable first step to validate the measures. However, quantitative measures are typically called upon to discriminate among devices.

In the present experiment, TRE and MO had the greatest influence on throughput. For this reason, we will concentrate on these two measures in analyzing the differences across devices. The averages for TRE and MO from Table 1 are illustrated in Figure 9. Note that performance is better as points move closer to the origin.


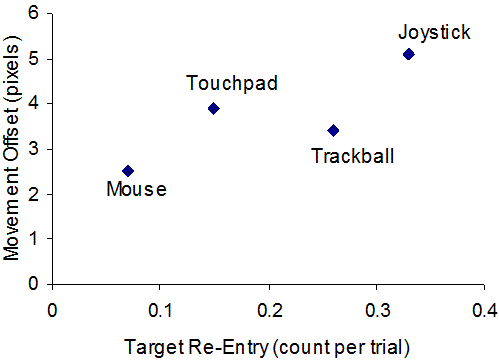
Figure 9. Device differences for target re-entry and movement offset

To test the discriminatory power of TRE and MO we conducted paired t-tests for all device combinations. Of the twelve possible comparisons (six for each measure), nine were significant. This confirms the ability of the measures to discriminate among devices.

The touchpad-trackball comparison is of particular interest because these devices had essentially the same throughput, as noted earlier. Figure 9 suggests that these two devices are different, based on TRE and MO. The difference in MO was not significant (t11 = 0.62, p > .05), whereas the difference in TRE was (t11 = 3.24, p < .01). Thus, while the throughput of these devices is similar, the touchpad is better when measured with TRE. Put another way, TRE reveals a problem with the trackball, in comparison to the touchpad, in its ability to position the pointer inside a target - and keep it there! This assessment is facilitated by the additional discriminatory power of the new accuracy measures, such as TRE.

CONCLUSIONS

Our goal in this study was to describe and validate new accuracy measures for computer pointing devices. We demonstrated that the proposed measures give information on pointing tasks beyond the traditional measures of speed, accuracy, and throughput. The latter are based on a single measurement per trial, and so are less adept at capturing movement behaviour during a trial.

The new measures are not intended to replace the traditional measures. Rather, we consider them supplementary measures, with the potential to explain why some devices are more efficient than others.

All of the proposed accuracy measures are associated with pointing device efficiency. As revealed in our "example" study, the efficiency of a pointing device suffers if movement control is difficult to the extent that the pointer must re-enter a target several times before selection. This conclusion follows from our measurement and analysis of target re-entries (TRE ). In addition, we showed by measuring and analysing movement offset (MO ) that the efficiency of pointing decreases if the pointer veers from the ideal path.

Target re-entry (TRE ) and movement offset (MO ) were the only accuracy measures related, independent of the other measures, to pointing device throughput. This does not mean that other measures are without merit. More likely, the importance of TRE and MO in this study may simply reflect the particular devices and/or task. In fact, the other measures may have a greater causal effect on throughput if adopted in studies with other devices or tasks (e.g., a stylus in a menu selection task).

An important result of the present study was that the accuracy measures with an independent contribution to pointing device throughput were able to discriminate among devices. Furthermore, in at least one comparison we found a significant difference between two devices even though those devices had essentially the same throughput, thus illustrating the discriminatory power of the new measures beyond that offered by throughput alone.

The new accuracy measures increase the theoretical knowledge base on subtle differences between various pointing devices. As we shift our focus from validating the measures to adopting them as tools in pointing device research, it is their causal link to device efficiency (viz. throughput) and their power to discriminate different devices that really counts. Both these capabilities have been established in this study.

ACKNOWLEDGEMENT

Many thanks to Hugh McLoone and William Soukoreff for comments and suggestions on this work.

REFERENCES

[1] Accot, J., and Zhai, S. Beyond Fitts' law: Models for trajectory-based HCI tasks, Proceedings of the CHI '97 Conference on Human Factors in Computing Systems. New York: ACM, 1997, pp. 295-302.

[2] Akamatsu, M., MacKenzie, I. S., and Hasbrouq, T. A comparison of tactile, auditory, and visual feedback in a pointing task using a mouse-type device, Ergonomics 38 (1995), 816-827.

[3] Bailey, R. W. Human performance engineering: Designing high quality, professional user interfaces for computer products, applications, and systems, 3rd ed. Upper Saddle River, NJ: Prentice Hall, 1996).

[4] Card, S. K., English, W. K., and Burr, B. J. Evaluation of mouse, rate-controlled isometric joystick, step keys, and text keys for text selection on a CRT, Ergonomics 21 (1978), 601-613.

[5] Douglas, S. A., Kirkpatrick, A. E., and MacKenzie, I. S. Testing pointing device performance and user assessment with the ISO 9241, Part 9 standard, Proceedings of the CHI '99 Conference on Human Factors in Computing Systems. New York: ACM, 1999, pp. 215-222.

[6] English, W. K., Engelbart, D. C., and Berman, M. L. Display selection techniques for text manipulation, IEEE Transactions on Human Factors in Electronics HFE-8 (1967), 5-15.

[7] Epps, B. W. Comparison of six cursor control devices based on Fitts' law models, Proceedings of the Human Factors Society 30th Annual Meeting. Santa Monica, CA: Human Factors Society, 1986, pp. 327-331.

[8] ISO ISO/TC 159/SC4/WG3 N147: Ergonomic requirements for office work with visual display terminals (VDTs) - Part 9 - Requirements for non-keyboard input devices, International Organisation for Standardisation, May 25, 1998.

[9] Karat, J., McDonald, J. E., and Anderson, M. A comparison of selection techniques: touch panel, mouse, and keyboard, Human-Computer Interaction--INTERACT '84. Elsevier Science Publishers, 1985, pp. 189-193.

[10]  MacKenzie, I. S. Fitts' law as a research and design tool in human-computer interaction, Human-Computer Interaction 7 (1992), 91-139.

[11] MacKenzie, I. S., Sellen, A., and Buxton, W. A comparison of input devices in elemental pointing and dragging tasks, Proceedings of the ACM Conference on Human Factors in Computing Systems - CHI '91. New York: ACM, 1991, pp. 161-166.

[12] Mithal, A. K., and Douglas, S. A. Differences in movement microstructure of the mouse and the finger-controlled isometric joystick, Proceedings of the ACM Conference on Human Factors in Computing Systems - CHI '96. New York: ACM, 1996, pp. 300-307.

[13] Murata, A. An experimental evaluation of mouse, joystick, joycard, lightpen, trackball, and touchscreen for pointing: Basic study on human interface design, Proceedings of the Fourth International Conference on Human-Computer Interaction. Elsevier, 1991, 123-127.

[14] Stevens, J. Applied multivariate statistics for the social sciences, 3rd ed. (Mahwah, NJ: Erlbaum, 1996).