---

Kabbash, P., MacKenzie, I. S., & Buxton, W. (1993). Human performance using computer input devices in the preferred and non-preferred hands. Proceedings of the ACM Conference on Human Factors in Computing Systems - INTERCHI '93, 474-481. New York: ACM. [software]

---

Human Performance Using Computer Input
Devices in the Preferred and
Non-Preferred Hands

Paul Kabbash¹, I. Scott MacKenzie², & William Buxton³

¹Computer Systems Research Institute
University of Toronto
Toronto, Ont. Canada M5S 1A4
416-978-1961, kabbash@dgp.toronto.edu

²Dept. of Computing & Information Science
University of Guelph
Guelph, Ont., Canada N1G 2W1
519-824-4120, mac@snowhite.cis.uoguelph.ca

³Univerity of Toronto & Xerox PARC,
c/o Computer Systems Research Institute
University of Toronto
Toronto, Ont. Canada M5S 1A4
416-978-1961, buxton@dgp.toronto.edu

Abstract
Subjects' performance was compared in pointing and dragging tasks using the preferred and non-preferred hands. Tasks were tested using three different input devices: a mouse, a trackball, and a tablet-with-stylus. The trackball had the least degradation across hands in performing the tasks, however it remained inferior to both the mouse and stylus. For small distances and small targets, the preferred hand was superior. However, for larger targets and larger distances, both hands performed about the same. The experiment shows that the non-preferred hand is more than a poor approximation of the preferred hand. The hands are complementary, each having its own strength and weakness. One design implication is that the non-preferred hand is well suited for tasks that do not require precise action, such as scrolling.

Keywords: Hand comparisons, computer input, Fitts' law.

INTRODUCTION

Increasingly, human-computer interaction supplements the familiar QWERTY keyboard with spatial controllers such as the mouse, stylus, or trackball. Nearly all such non-keyboard devices are operated with the preferred, "dominant" hand only. This contrasts with the everyday world, where the non-dominant hand is also used to perform spatial tasks. If one wants to design user interfaces to capture this common skill, there is little in the literature to serve as a guide.

This paper explores the performance of the non-preferred hand when interacting with various computer input devices for pointing, selecting, and dragging tasks. It is a repeat of an earlier experiment [11], that investigated the preferred hand in these same tasks. We compare performance across hands for three input devices: mouse, trackball, and stylus. The metrics for comparison in the present report are movement time and accuracy.

PREVIOUS RESEARCH

This study builds upon previous research in three distinct areas: Fitts' law models for psychomotor behavior, lateral asymmetries, and HCI. On its own, each is represented in the literature; however, only a few studies have attempted to reconcile issues of mutual interest.

Fitts' Law Models

One of the most robust and highly adopted models of human movement is Fitts' law [4, 5]. The model is, arguably, the most successful of many efforts to model human behavior as an information processing activity. (For detailed reviews, see [10, 12, 20].) Fitts was interested in applying information theory to measure the difficulty of movement tasks and the human rate of information processing as tasks are realized. Fitts argued that the amplitude of a move was analogous to electronic signals and that the spatial accuracy was analogous to electronic noise. He proposed that the "index of difficulty" (ID) of a movement task could be measured in "bits" as the logarithm of the amplitude moved (A) divided by the tolerance or width (W) of the region within which the move terminates.

In this paper, we use the Shannon formulation for the index of task difficulty [10]:

ID = log2(A/W + 1).

(1)

In calculating ID, we adjust target width to reflect the spatial distribution of responses. This is in keeping with the information theoretic premise of the law, in which target width is analogous to a Gaussian distributed "noise" perturbing the intended signal (i.e., amplitude). The normalized target width is usually called the "effective target width," W_e [10].

Lateral Asymmetries

Three theories have been proposed to account for the between-hand performance differences in rapid aimed movements.

The first is that preferred and non-preferred hands differ primarily in their use of sensory feedback control [6, 17, 21]. In expounding this theory, Flowers [6] contrasted "ballistic" and "controlled" movements. He found that the preferred and non-preferred hands of strongly lateralized subjects achieved equal rates in a rhythmic tapping task, but that in a variation of Fitts' reciprocal tapping task (ranging from ID = 1 to ID = 6) the preferred hand outperformed the non-preferred hand by 1.5 - 2.5 bits/s, with differences marked at all but the lowest two IDs.

A second theory is that the preferred hand is less "noisy" in its output function. Accordingly, increases in movement amplitude or decreases in movement time require a greater force, which leads to greater output variability and thus more errors [16]. Annett et al. [1] suggested that this theory could be adapted to account for differences between hands in a peg transfer activity in which movement time was a dependent variable.

A third model, which predicts a left-hand advantage for larger target distances, was suggested by Todor and Doane [18]. This model, in a sense, expands on Flowers' notion of feedback control by incorporating both a left-hemisphere/right-hand superiority for sequential processing, and a right-hemisphere/left-hand superiority for non-adaptive parallel processing. The model was based on Welford's proposal that rapid aimed movements are composed of two distinct parts: a "fast distance-covering phase and a slower phase of 'homing' on to the target" [20]. The first phase is similar in speed to ballistic movement, but the second phase requires an additional process of visual control. They hypothesized, assuming contralateral control for the movements, that the right and left hands should exhibit a performance advantage in task conditions favoring the dominant processing mode of the contralateral hemisphere; specifically, that within tasks of equivalent calculated difficulty, movement time in the right hand should increase as the width and amplitude of the target grows larger while it should decrease in the left hand.

Although the association between motor programming and the spatial complexity of a task has been questioned in the literature, particularly by Quinn et al. [19], our interest in the Todor and Doane model is primarily in the practical result. In designing computer interfaces that allow for separate input from the non-preferred hand, it is useful to discern features of the task, aside from difficulty, that give a consistent advantage (or disadvantage) to the non-preferred hand. The issue of program complexity in itself, however, will not be directly addressed.

Human-Computer Interaction

A number of studies have been published which compare the usage of various input devices. This literature is effectively surveyed elsewhere [7, 13]. However, we have found few studies that compare performance of the dominant vs. non-dominant hand in spatial tasks. An exception is Boritz, Booth, and Cowan [2] who tested a group of left-handed subjects and a group of right-handed subjects in a simple target selection task. Their study was flawed, however, in that the left-handed group had considerable prior experience using the mouse in the right hand, owing to the forced position of the mice in the computer lab.

Buxton and Myers [3] performed two experiments examining two-handed input. In the first, the non-dominant hand scaled an object while the dominant hand positioned it. In the second, the non-dominant hand navigated (scroll and jump) through a document while the dominant hand selected specified pieces of text. These experiments clearly demonstrated that users could easily use the non-dominant hand in such tasks.

MacKenzie, Sellen, and Buxton [11] showed that Fitts' law was applicable beyond traditional target acquisition tasks to include tasks such as dragging. This experiment provided half of the data for the current study. It tested the mouse, trackball, and tablet-with-stylus and found performance decrements for dragging compared to pointing. This degradation was concluded to be due to interference between the target acquisition task and maintenance of the dragging state (for example, holding down the mouse button while dragging). This degradation was found on each device for the criterion variables movement time and error rate. The amount of degradation was not uniform across devices, however. Significant one-way effects and two-way interactions revealed that the trackball was more prone to errors during dragging. Movement time was significantly longer for the trackball on both tasks; however the degradation during dragging was more pronounced for the mouse than for the trackball or stylus.

The experiment described in the next section emerged from the following hypotheses:

H1	Preferred and non-preferred hands yield the same speed, accuracy, and bandwidth using the mouse, trackball, and stylus in pointing and dragging tasks.
H2	Devices using small muscle groups (e.g., trackball) produce smaller differences between hands than devices using large muscle groups (e.g., mouse & stylus).

Of course, the first hypothesis is a null statement leading to the usual statistical tests. Differences were fully expected. A major motivation in the present study was to determine the extent of such differences.

METHOD

Subjects

In all we tested 24 subjects, comprising two independent groups of 12 (11 male, 1 female in Group 1; 9 male, 3 female in Group 2). The two groups, computer literate staff or students from local universities, served as paid volunteers. All subjects were self-declared right handers; but as an additional criterion for Group 2 we administered the Edinburgh Inventory for handedness [14], requiring a laterality quotient of at least +80.

Apparatus

The two groups were tested at different times, but on identical equipment. Subjects performed the tasks on an Apple Macintosh II using three input devices: the standard mouse, a Wacom tablet-with-stylus (model SD42X) used in absolute mode with a pressure sensitive stylus, and a Kensington trackball (model Turbo Mouse ADB Version 3.0). The equipment was set up with the input device on the right of the keyboard for Group 1 and on the left for Group 2. All devices were adjusted for a control/display ratio of approximately 0.5.

Procedure

Subjects performed multiple trials on two different tasks with three different devices using their right hand (Group 1) or left hand (Group 2). The operation of the devices and the requirements of the tasks were explained and demonstrated to each subject before beginning. One warm-up block of trials was given prior to data collection.

The two tasks were "point-select" and "drag-select." For the point-select task, shown in Figure 1a, subjects moved the cross-hair cursor (+), back and forth between the targets and selected each target by pressing and releasing a button on the mouse or trackball, or by applying and releasing pressure on the stylus.

(a)     (b)
Figure 1. Experimental tasks were (a) pointing and (b) dragging.

The arrow in Figure 1a pointed to the target to be selected. This helped maintain stimulus-response (S-R) compatibility as subjects proceeded. For the dragging task (Figure 1b), subjects acquired the small diamond-shaped object by pressing and holding the device button (on the mouse and trackball) or maintaining pressure on the stylus, and then dragged the object to the other target and deposited the object in the target region by releasing the button or pressure.

Subjects were instructed to balance speed and accuracy for an error rate around 4%. The software generated a beep as feedback for monitoring target misses.

Design

A 2 × 4 × 4 × 3 × 2 (Hand × Amplitude × Width × Device × Task) factorial design with repeated measures was used. Hand was a between-subjects factor, with Group 1 tested on their right (preferred) hand and Group 2 tested on their left (non-preferred) hand. All other factors were within-subjects. The A-W conditions were chosen to exactly mimic Fitts' [4] original experiments with a stylus. There were four levels each for A (64, 128, 256, or 512 pixels) and W (8, 16, 32, or 64 pixels).

The A-W conditions were presented in random order with a block of ten trials performed at each condition. A session consisted of a sequence of sixteen blocks covering all A-W conditions. Ten sessions were sequenced for each device, alternating between pointing (five sessions) and dragging (five sessions). The initial task was chosen by the toss of a coin. Device ordering was counterbalanced.

The system collected three measurements for each trial: movement time and the x and y selection coordinates. Dependent variables were movement time, bandwidth, error rate, variable error, and constant error. Each of the accuracy measures describes different response behaviors (see, for example, [12]).

Constant error is the mean deviation of responses from the target center. Constant error quantifies systematic biases of the responses from the target center; i.e., the tendency to overshoot or undershoot the targets.

Variable error is the standard deviation of movement endpoints along the horizontal axis. This corresponds to effective target width (W_e = 4.133 × SD_x; see [10]). There are important distinctions between variable error and error rate despite their high correlation in Fitts' law tasks when error rates are below about 15% [9]. Error rate is especially relevant in HCI research, in the sense that the human operator is interested only in the success or failure in performing an operation, not in whether the effort was, for example, a near or far miss. Variable error, however, captures endpoint variability over all movements and so describes more completely the behavior.

Bandwidth, a composite of movement time and variable error, is a dependent variable meriting a separate analysis. Due to space limitations, bandwidth is not discussed further in the present paper.

RESULTS

Adjustment of Data

Newman-Keuls tests were performed on the session means at each Hand × Device × Task condition for the first three dependent variables (36 tests). Overwhelmingly, the first session differed from groupings of sessions 2-5, and sessions 2-5 did not differ among themselves; and so, the data from the first session were discarded.

On the remaining data, using the same decomposition, outlier trials were eliminated where the x-coordinate was more than three standard deviations from the mean. We also eliminated trials immediately following deviate trials (see [15]).

Movement Time (MT)

For each dependent variable an analysis of variance was used with repeated measures on device and task. Mean movement times for the two hands are summarized in Table 1, decomposed by device and task. As expected, the right hand outperformed the left hand (F_1,22 = 15.5, p < .001) with overall movement times of 889 ms and 1044 ms, respectively.

Left Hand Right Hand Both Hands ----------------- ----------------- ----------------- Point Drag Both Point Drag Both Point Drag Both --------------------------------------------------------------------- Mouse 879 1084 982 657 900 779 768 992 880 Stylus 814 1021 917 645 786 716 729 904 817 Trackball 1165 1301 1233 1079 1266 1172 1122 1283 1203 --------------------------------------------------------------------- Column means 953 1135 1044 794 984 889 873 1060 967

Table 1. Mean movement time (ms) by device, task, and hand.

The main effects of device and task were highly significant (F_2,44 = 273, p < .001 and F_1,22 = 124, p < .001, respectively). The effect of task was reflected in much slower MT for dragging (1060 ms) than pointing (873 ms). There was, however, no interaction of Hand × Task (F_1,22 = .044, ns), and performance in both hands degraded equally. For each hand the slowest device by far was the trackball with performance on the other two devices slowing somewhat from stylus to mouse. A significant interaction of Hand × Device (F_2,44 = 10.7, p < .001) can be attributed to the trackball. That is, from preferred to non-preferred hand the degradation in mouse and stylus was large but equal (roughly 27%), whereas there was no difference in MT between hands on the trackball (F_1,22 = 1.52, p > .05). There was also a significant three-way interaction of Hand × Device × Task (F_2,44 = 4.33, p < .05), one interpretation being that, although left-hand MT degraded equally in mouse and stylus going from the pointing task to dragging, the right hand showed greater degradation in the mouse than either the stylus or the trackball.

The effect of amplitude and width on movement time was investigated at each level of difficulty. As predicted by Todor and Doane [18], there was a tendency for left-hand MT to decrease as A and W increased within each ID level and, conversely, for right-hand MT to increase. The decreases in the left hand were in general larger and more consistent than the increases in the right hand, particularly so for the mouse. The effect, seen in Figure 2, extends Todor and Doane's results to a wide range of task difficulties. Their subjects, tested for two task conditions at ID = 6 bits, also failed to show significant MT increases in the right hand. As Todor reasoned, this may be due to differential training.

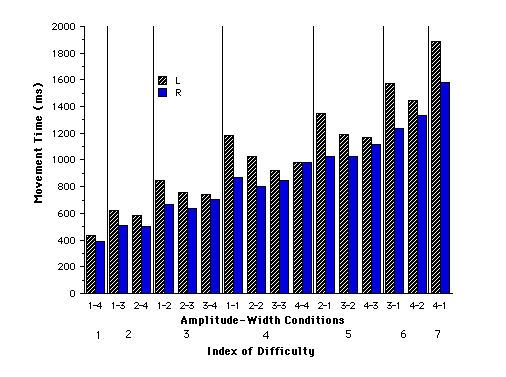
Figure 2. Movement time (ms) by amplitude, width, and hand.

First number of amplitude-width combinations refers to amplitude and second number refers to target width. For amplitude, 1 = 64 pixels, 2 = 128 pixel, 3 = 256 pixels, and 4 = 512 pixels. For target width, 1 = 8 pixels, 2 = 16 pixels, 3 = 32 pixels, and 4 = 64 pixels.

Comparing performance across index of difficulty in Figure 2, it can also be seen that, in agreement with Flowers' feedback control theory, the right hand gained an advantage as target widths grew narrower (for example, conditions 1-4, 1-3, 1-2, 1-1). However, the L – R differences did not change when target amplitudes increased while target width was held constant (for example, conditions 1-4, 2-4, 3-4, and 4-4). Spatial target conditions, rather than task difficulty per se, therefore appear to have accounted for the between-hand MT differences.

Accuracy

Error Rate. The two subject groups performed at comparable error rates throughout, except for two device-task combinations (mouse-dragging, where the right hand was superior, and trackball-dragging, where the left hand was superior).

Table 2 summarizes the mean percentage errors by hand, device, and task. In support of H1, error rates did not differ between the hands with means of 7.9% for the preferred hand and 8.0% for the non-preferred hand (F_1,22 = .005, ns). Both hands were far more accurate during pointing than dragging. Error rates during the pointing task were within the desired range of 4% with means of 3.2% in the right hand and 3.6% in the left hand, but were considerably higher for dragging with means of 12.6% and 12.5%, respectively. Although the main effect of task was highly significant (F_1,22 = 138, p < .001), degradation in the two hands was equal over tasks as evidenced by a lack of Hand × Task interaction (F_1,22 = .102, ns). In contrast, the two-way interaction of Hand × Device was significant (F_2,44 = 3.93, p < .05) with accuracy from the right to left hand degrading in the mouse and stylus but improving in the trackball. This supports H2.

Left Hand Right Hand Both Hands ----------------- ----------------- ----------------- Point Drag Both Point Drag Both Point Drag Both ------------------------------------------------------------------------ Mouse 3.0 12.0 7.5 2.8 9.8 6.3 2.9 10.9 6.9 Stylus 4.9 12.7 8.8 3.6 12.2 7.9 4.3 12.5 8.4 Trackbail 2.8 12.6 7.7 3.3 15.8 9.6 3.0 14.2 8.6 ------------------------------------------------------------------------ Column means 3.6 12.5 8.0 3.2 12.6 7.9 3.4 12.5 8.0

Table 2. Mean error rates (%) by device, task, and hand.

As mentioned, the last result is mostly attributable to differences while dragging with the mouse and trackball. Error rate was also slightly higher in the left hand while pointing with the stylus (4.9% vs. 3.6%), but this is probably due to the difficulty many subjects reported in controlling the pen's pressure activated switch with their non-preferred hand. All subjects from Group 2 experienced problems with pen slippage when making target selections during the pointing task, and they applied much more force than necessary to activate the switch.

Effective Target Width. Analysis of this dependent variable was directed to the hypothesis of Annett et al. [1] that superior preferred-hand performance for controlled movements is attributable to a greater motor-output variability in the non-preferred hand. Unlike the mouse and the stylus, the trackball showed a significant Hand × Task interaction (mouse, F_1,22 = .565, ns; stylus, F_1,22 = .100, ns; trackball, F_1,22 = 7.04, p < .05). This is shown in Table 3. Whereas results in the right hand for trackball-pointing proved similar to those in mouse and stylus, trackball-dragging yielded a large left-hand advantage, both in mean scores and standard deviations, which was especially apparent at the smallest width. At all target widths in Table 3, the left-hand dragging condition displayed less variable error than the right-hand dragging condition.

W = 8 W = 16 W = 32 W = 64 All Widths ----------------------------------------------------------- Left Hand Pointing 9.2 16.1 29.4 56.4 27.7 Dragging 14.2 24.0 43.6 77.5 39.8 Right Hand Pointing 9.4 14.8 26.8 49.7 25.2 Dragging 33.7 39.1 54.6 84.2 52.9

Table 3. Mean effective target width (W_e, in pixels) for the trackball by task and W.

The motor-output variability theory predicts that larger target amplitudes should result in either a greater lengthening of movement time in the non-preferred hand or a greater degradation of variable error. Neither result held in the stylus, while only moderate support was found in the mouse. The finding of superior left-hand We for the trackball was unexpected and will be discussed below.

Constant Error. Table 4 summarizes constant error by device, task, and hand. Both hands exhibited a small tendency to undershoot the center of the target in all combinations, except for stylus-dragging where the two hands had a similar tendency to overshoot the target. Biases were small, on average falling within one pixel of target center. For all data, the main effect of hand was not significant (F_1,22 = .485, ns). For subsets of the data by device, the effect of hand was significant only for the trackball (F_1,22 = 4.49, p < .05). This was again due to the dragging task, where the left hand showed greater accuracy (CE = -0.143 pixels vs. -2.38 pixels).

Mouse Stylus Trackball ------------------------------------------ Left Hand Pointing -1.11 -0.31 -0.98 Dragging -0.16 +0.75 -0.14 Right Hand Pointing -1.16 -0.42 -0.82 Dragging +0.49 +1.06 -2.38

Table 4. Constant error (pixels) by device, task, and hand.

DISCUSSION

The most important finding of the study is how the results for movement time essentially extended the findings of Todor and Doane [18]. In tasks of equivalent difficulty, between-hand comparisons showed a right-hand advantage for target width, but a left-hand advantage for amplitude. This held in spite of the traditional Fitts prediction for equal movement time in a given limb system, when the spatial conditions of a task calculate to the same ID.

We found nothing in the analysis of accuracy to indicate that this main result was influenced by different speed-accuracy tradeoffs in the two hands. All accuracy measures were in fact largely independent of hand (with some exceptions during mouse-dragging and trackball-dragging). In the case of error rate this is not surprising, since the two subject groups were instructed to monitor performance by error-rate feedback.

Nonetheless, the three accuracy measures used in the experiment clearly captured distinct aspects of subject behavior. Constant error was most sensitive to the mechanical differences between devices. Stylus-pointing yielded smaller constant error than either mouse-pointing or trackball-pointing, presumably because subjects were able to place the stylus on the tablet with pen-point precision as opposed to the trackball technology of the mouse and the trackball; conversely, the mouse and trackball were more accurate than the stylus during dragging (excluding trackball-dragging in the right hand). This was largely due to subjects inadvertently lifting the stylus tip off of the tablet surface while dragging.

Error rate most clearly captured the difficulty of the dragging task. As was seen, both groups settled for much higher error rates during dragging, probably because subjects were unwilling to slow down sufficiently for this task, given their relative success with the pointing task. Only the right-hand group, however, showed unequal degradation between devices.

Going from pointing to dragging in the right hand, error rate for the mouse degraded least of the three devices while movement time degraded most. However, the lack of Hand × Task interaction on W_e in the mouse implies that the right-hand group was no less variable during the dragging task, just more careful. The speed-accuracy tradeoff here was most likely an experimental artifact – a side effect of daily work habits­p;in that all subjects had experience on the mouse but not on the other devices.

Finally, the peculiar results for accuracy during the trackball-dragging condition appear to have captured some underlying asymmetry in the motor function of the two hands. Here all three accuracy measures displayed a large left-hand advantage. Trackball-dragging also showed poor accuracy only in the right hand, in the sense that the left hand was equally accurate across devices when dragging.

Based on earlier results [11], it was speculated that device differences may be attributed to the extent of interference between the muscle groups required to manipulate a device, in particular, that finger-thumb interference would be greater than wrist-finger interference, and that this would contribute to superior performance in the mouse or stylus relative to the trackball. Our results for accuracy in the trackball confirm that finger-thumb independence was a significant requirement for trackball-dragging, but that it primarily affected the right hand. This may be compared to the finding by Kimura [8] that right-handers perform paired finger flexions more easily with their left hand; both results point to superior fine motor control in the left hand. The poor speeds achieved with the trackball in the present experiment, therefore, may simply have been a function of "ceiling effects" for this device. In spite of this, ceiling effects were not found to affect differential accommodations with respect to spatial target conditions on either task. In fact, of the three devices tested, the trackball most clearly supported the Todor and Doane theory.

CONCLUSION

The above provides the foundation on which design decisions can be based. First, for rough pointing or motion, the non-dominant hand is as good as the dominant hand across a large range of task difficulties. Therefore, it is appropriate for tasks that do not require precise action, such as scrolling (for example, as used in [3]). If the non-dominant hand is used for pointing, wide targets should be used.

While there was the least change between hands with the trackball, non-dominant performance with the mouse was still far superior. Readers are cautioned not to draw from this that if one is to use both hands that two mice are the best design choice. The ease of acquiring a fixed position device (such as a trackball, touch pad, or joystick) may more than compensate for slower task performance once acquired. This is something that must be evaluated in context of the specific task.

ACKNOWLEDGMENTS

We would like to thank the members of the Input Research Group at the University of Toronto who provided the forum within which this work was undertaken. Thanks also to Dan Russell for his comments on the manuscript. Primary support for this work has come from Digital Equipment Corp., Xerox PARC, and the Natural Sciences and Engineering Research Council of Canada. Additional support has been provided by Apple Computer Inc., IBM Canada's Laboratory Centre for Advanced Studies, and the Arnott Design Group of Toronto. This support is gratefully acknowledged.

REFERENCES

1. Annett, J., Annett, M., Hudson, P. T. W., & Turner, A. (1979). The control of movement in the preferred and non-preferred hands. Quarterly Journal of Experimental Psychology, 31, 641-652.

2. Boritz, J., Booth, K. S., & Cowan, W. B. (1991). Fitts's law studies of directional mouse movement. Proceedings of Graphics Interface '91, Toronto: Canadian Information Processing Society, 216-223 .

3. Buxton, W., & Myers, B. A. (1986). A study in two-handed input. Proceedings of the CHI '86 Conference on Human Factors in Computing Systems . New York: ACM, 321-326.

4. Fitts, P. M. (1954). The information capacity of the human motor system in controlling the amplitude of movement. Journal of Experimental Psychology, 47, 381-391.

5. Fitts, P. M., & Peterson, J. R. (1964). Information capacity of discrete motor responses. Journal of Experimental Psychology, 67, 103-112.

6. Flowers, K. (1975). Handedness and controlled movement. British Journal of Psychology, 66, 39-52.

7. Greenstein, J. S., & Arnaut, L. Y. (1988). Input devices. In M. Helander (Ed.), Handbook of human-computer interaction. Amsterdam: Elsevier, 495-519.

8. Kimura, D., & Vanderwolf, C. H. (1970). The relation between hand preference and the performance of individual finger movements by left and right hands. Brain, 93, 769-774.

9. MacKenzie, I. S. (1991). Fitts' law as a performance model in human-computer interaction. Doctoral dissertation. University of Toronto.

10. MacKenzie, I. S. (1992). Fitts' law as a research and design tool in human-computer interaction. Human-Computer Interaction, 7, 91-139.

11. MacKenzie, I. S., Sellen, A., & Buxton, W. (1991). A comparison of input devices in elemental pointing and dragging tasks. Proceedings of the CHI '91 Conference on Human Factors in Computing Systems , New York: ACM, 161-166. .

12. Meyer, D. E., Smith, J. E. K., Kornblum, S., Abrams, R. A., & Wright, C. E. (1990). Speed-accuracy tradeoffs in aimed movements: Toward a theory of rapid voluntary action. In M. Jeannerod (Ed.), Attention and Performance XIII , Hillsdale, NJ.: Erlbaum, 173-226. .

13. Milner, N. (1988). A review of human performance and preferences with different input devices to computer systems. In D. Jones & R. Winder (Eds.), People and Computers IV, Proceedings of the Fourth Conference of the British Computer Society Human-Computer Interaction Specialist Group (pp. 341-362). Cambridge: Cambridge University Press.

14. Oldfield, R. C. (1971). The assessment and analysis of handedness: The Edinburgh inventory. Neuropsychologia, 9, 97-113.

15. Rabbitt, P. M. A. (1968). Errors and error correction in choice-response tasks. Journal of Experimental Psychology, 71, 264-272.

16. Schmidt, R. A., Zelaznik, H., Hawkins, B., Frank J. S., & Quinn, J. T. (1979). Motor-output variability: A theory for the accuracy of rapid motor acts. Psychological Review, 86, 415-451.

17. Sheridan, M. R. (1973). Effects of S-R compatibility and task difficulty on unimanual movement time. Journal of Motor Behavior, 5, 199-205.

18. Todor, J. I., & Doane, T. (1978). Handedness and hemispheric asymmetry in the control of movements. Journal of Motor Behavior, 10, 295-300.

19. Quinn, J. T., Zelaznik, H. N., Hawkins, B., & McFarquhar, R. (1980). Target-size influences on reaction time with movement time controlled. Journal of Motor Behavior, 12, 239-261.

20. Welford, A. T. (1968). Fundamentals of skill. London: Methuen.

21. Woodworth, R. S. (1899). The accuracy of voluntary movements. Psychological Review [monograph supplement], 3(2, Whole No. 13).