MacKenzie, I. S. (1995). Movement time prediction in human-computer interfaces. In R. M. Baecker, W. A. S. Buxton, J. Grudin, & S. Greenberg (Eds.), Readings in human-computer interaction (2nd ed.) (pp. 483-493). Los Altos, CA: Kaufmann. [reprint of MacKenzie, 1992] [software]
Movement Time Prediction in Human-Computer Interfaces
I. Scott MacKenzie
Department of Computing and Information ScienceUniversity of Guelph
Guelph, Ontario, Canada N1G 2W1
519-824-4120, mac@snowhite.cis.uoguelph.ca
Abstract
The prediction of movement time in human-computer interfaces as undertaken using Fitts' law is reviewed. Techniques for model building are summarized and three refinements to improve the theoretical and empirical accuracy of the law are presented. Refinements include (1) the Shannon formulation for the index of task difficulty, (2) new interpretations of "target width" for two- and three-dimensional tasks, and (3) a technique for normalizing error rates across experimental factors. Finally, a detailed application example is developed showing the potential of Fitts' law to predict and compare the performance of user interfaces before designs are finalized.Keywords: human performance modeling, Fitts' law, input devices, input tasks
Introduction
Movement is ubiquitous in human-computer interaction. Our arms, wrists, and fingers busy themselves on the keyboard and desktop; our head, neck, and eyes move about attending to graphic details recording our progress. Matching the movement limits and capabilities of humans with interaction techniques on computing systems, therefore, can benefit from research in this important dimension of human behaviour.
One focus in HCI research is in predicting and modelling the time for humans to execute tasks. Although encompassing a vast territory to be sure, one dimension is the time invested in movement. In fact, movement is an integral, seemingly innocuous component of many research questions in HCI: Are popup menus superior to menu bars? Which input device affords the quickest and most accurate interaction? Should a scroll bar in a text editor be on the left or right side of the CRT display? Can gestures replace commands in text editing?
In this review paper, we will explore Fitts' law, a powerful model for the prediction of movement time in human-computer interaction. We are motivated by (a) apparent problems in previous work, (b) the difficulty in interpreting and comparing published results, and (c) the need to guide future research using Fitts' law.
We begin with a brief tour of Fitts' law, and follow by describing some refinements to correct flaws or to improve its prediction power. Finally, derived models are used in an application example to illustrate the potential of Fitts' law in assessing and comparing interface scenarios before they are finalized in products.
A Brief Tour of Fitts' Law
The application of information theory to human performance modeling dates to the 1950s when experimental psychologists (e.g., Miller, 1953) embraced the work of Shannon, Wiener, and other information theorists as a framework for understanding human perceptual, cognitive, and motor processes. Models, or "laws", that persist today include the Hick-Hyman law for choice reaction time (Hick, 1952; Hyman, 1953) and Fitts' law for movement time (Fitts, 1954; Fitts & Peterson, 1964).
According to Fitts, a movement tasks' difficulty (ID, the "index of difficulty") can be quantified using information theory by the metric "bits". Specifically,
| ID = log2(2A / W) | (1) |
where A is the distance or amplitude to move and W is the width or tolerance of the region within which the move terminates. Because A and W are both measures of distance, the term within the parentheses in Equation 1 is without units. The unit "bits" emerges from the somewhat arbitrary choice of base 2 for the logarithm. From Equation 1, the time to complete a movement task is predicted using a simple linear equation, where movement time (MT) is a linear function of ID.
Figure 1 shows the serial tapping task used by Fitts (1954). In this experiment, subjects alternately tapped as quickly and accurately as possible between two targets of width W at a distance A. Obviously, as targets get farther away or as they get smaller, the tasks get more difficult and more time is required to complete the task. In Fitts' experiment A and W each varied over four levels. The easiest task had A = 1 inch and W = 1 inch for ID = log2(2A / W) = log2(2) = 1 bit. The hardest task had A = 16 inches and W = 0.25 inches for ID = log2(128) = 7 bits.
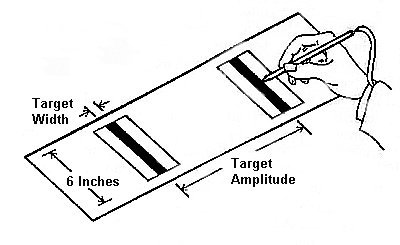
Figure 1. The serial tapping task used by Fitts (1954).
The task in Figure 1 can be implemented on interactive graphics systems using targets displayed on a CRT and a cursor manipulated by an input device. A common variation is the discrete task — a single movement toward a target from a home position (see Figure 2). Target selection is usually accomplished by a button push when the cursor is over the target.
The first use of Fitts' law in HCI research was the work of Card, English, and Burr (1978) who applied the model on data collected in a text selection task using a joystick and a mouse. Subjects were required to move the cursor from a home position to a target — a word — and select it by pushing a button. Numerous other HCI researchers have subsequently used Fitts' law. Examples include Boritz, Booth, and Cowan (1991); Gillan, Holden, Adam, Rudisill, and Magee (1990); Card, Mackinlay, and Robertson (1990); Epps (1986); MacKenzie, Sellen, and Buxton (1991); Walker and Smelcer (1990); and Ware and Mikaelian (1987).
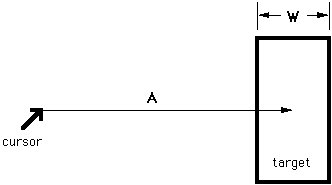
Figure 2. A discrete task using a cursor and a target displayed on a CRT.
A movement model based on Fitts' law is an equation predicting movement time (MT) from a task's index of difficulty (ID). Figure 3 shows the general idea.
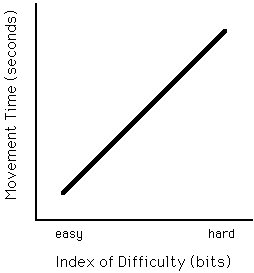
Figure 3. Movement time prediction.
As expected, movement time for hard tasks is longer than for easy tasks. The prediction equation for the line in Figure 3 is of the form
| MT = b × ID | (2) |
or
| MT = a + b × ID | (3) |
depending on whether or not the line goes through the origin. In both cases, b is the slope of the line.
Since task difficulty is analogous to information, the rate of task execution can be interpreted as the human rate of information processing. For example, if a task rated at, say, ID = 4 bits is executed in 2 seconds, then the human rate of information processing is 4 / 2 = 2 bits/s. This is also evident by examining Figure 3. Since the vertical and horizontal axes carry the units "seconds" and "bits" respectively, the slope of the line is in "seconds/bit". The reciprocal of the slope is in "bits/s". The latter measure Fitts called the index of performance (IP). Since IP is in bits/s, the term "bandwidth" is also used.
Intuitively, the higher the bandwidth the higher the rate of human performance since more information is being articulated per unit time. One of the strengths in Fitts' law is that measures for IP, or bandwidth, can motivate performance comparisons across factors such as device, limb, or task. It follows that performance in a human-computer interface can be optimized by selecting and combining those conditions yielding high bandwidths.
Equation 2 is ideal since the prediction line goes through the origin. This is important for the intuitive reason that a movement task rated at ID = 0 bits is predicted by Equation 2 to take zero seconds, as desired. By Equation 3, however, a non-zero intercept implies that a task rated at ID = 0 bits will take "a" seconds to execute. (This point will surface again later.)
Building a Fitts' Law Model
In building a Fitts' law model, the slope and intercept coefficients in the prediction equation are determined through empirical tests. The tests are undertaken in a controlled experiment using a group of subjects and one or more input devices and task conditions. On interactive computing systems, this could range from manipulating a cursor with a mouse and selecting icons to manipulating a virtual hand with an input glove and grabbing objects in a 3D virtual space.
The design of experiments for Fitts' law studies is simple. Tasks are devised to cover a range of difficulties by varying A and W. For each task condition, multiple trials are conducted and the time to execute each is recorded and stored electronically for statistical analysis. Errors are also recorded (and analysed as discussed later). Generally, measurements are aggregated across subjects resulting in one data point for each task condition. A typical data set is shown in Table 1 for a stylus in a serial point-select task mimicking Fitts' serial tapping task (MacKenzie, 1991).
Data From an Experiment Using a
Stylus in a Point-Select Task
| Aa | Wa | ID (bits) | MT (ms) | Error (%) | IP (bits/s) |
|---|---|---|---|---|---|
| 8 | 8 | 1 | 254 | 0.0 | 4.3 |
| 8 | 4 | 2 | 353 | 1.9 | 6.1 |
| 16 | 8 | 2 | 344 | 0.8 | 6.4 |
| 8 | 2 | 3 | 481 | 1.7 | 6.4 |
| 16 | 4 | 3 | 472 | 2.1 | 6.6 |
| 32 | 8 | 3 | 501 | 0.6 | 6.2 |
| 8 | 1 | 4 | 649 | 8.8 | 6.3 |
| 16 | 2 | 4 | 603 | 2.1 | 6.8 |
| 32 | 4 | 4 | 605 | 2.7 | 6.7 |
| 64 | 8 | 4 | 694 | 2.5 | 5.9 |
| 16 | 1 | 5 | 778 | 7.0 | 6.6 |
| 32 | 2 | 5 | 763 | 3.4 | 6.6 |
| 64 | 4 | 5 | 804 | 2.3 | 6.3 |
| 32 | 1 | 6 | 921 | 8.5 | 6.6 |
| 64 | 2 | 6 | 963 | 3.3 | 6.3 |
| 64 | 1 | 7 | 1137 | 9.9 | 6.3 |
| Mean | 645 | 3.6 | 6.3 | ||
| SD | 243 | 3.1 | 0.6 | ||
| a experimental units; 1 unit = 8 pixels | |||||
The first three columns contain the independent variables target amplitude (A), target width (W), and the associated index of difficulty (ID) calculated using Equation 1. A and W each varied over four levels, yielding IDs of 1 to 7 bits. In the last three columns are the dependent variables movement time (MT), error rate, and the index of performance (IP = ID / MT). Each row entry is the mean of about 470 trials. The grand means were 645 ms for movement time, 3.6% for error rate, and 6.3 bits/s for the index of performance, as shown in the second last row.
The next step in model building is to enter the 16 MT-ID points in tests of correlation and linear regression. The data in Table 1 yield a regression line with movement time (ms) predicted as
| MT = 53 + 148 × ID | (4) |
with a correlation of r = .992. Correlations above .900 are considered very high for any experiment involving measurements on human subjects. A high r suggests that the model provides a good description of observed behaviour.
The prediction equation has an intercept of 53 ms and a slope of 148 ms/bit. Converting the slope to its reciprocal yields an index of performance, or bandwidth, of 6.8 bits/s. Often the data points and regression line are shown together in a scatter plot (see Figure 4).
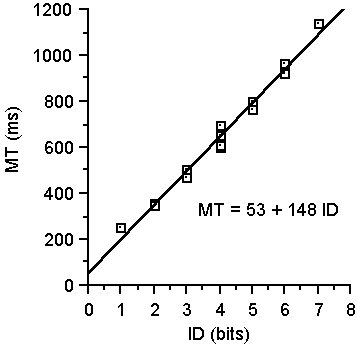
Figure 4. Scatter plot and regression line for the data in Table 1.
As just shown, the index of performance can be calculated using a direct division of mean scores (IP = ID/MT) or through linear regression (IP = 1 / b, from MT = a + b ID). The two methods yielded slightly different results: 6.3 bits/s using the direct method vs. 6.8 bits/s using the slope reciprocal. Although the disparity seems small, the correct method of calculation is in doubt. Fitts used the direct method in his 1954 paper and linear regression in a subsequent study (Fitts & Peterson, 1964). Most (but not all) current researchers use linear regression. Notably, the disparity is systematic: If the line in Figure 4 is rotated counter-clockwise forcing it through the origin, the slope increases and the slope reciprocal decreases, thus reducing the disparity.
If the regression line intercept is small the difference between the two bandwidth measures will be slight. If the intercept is large, the difference may be appreciable. In the latter case, a consistent, additive component of the task (such as a button push) may be the source of the intercept.
An example is the model built by Card et al. (1978) for the mouse in a text selection task:
| MT = 1030 + 96 × ID | (5) |
Although the fit was again very good (r = .91), this equation has one of the largest intercepts in published Fitts' law research. The implication, of course, is that a movement task rated at ID = 0 bits will take 1.03 seconds.
The large intercept also casts doubt on the validity of the slope reciprocal as a measure for bandwidth. The slope of 96 ms/bit translates into a bandwidth of 10.4 bits/s. The Card et al. (1978) experiment used 20 task conditions with a mean ID of 2.63 bits/s. The mean movement time was reported as 1.29 s; so, the bandwidth calculated using a direct division of means is 2.63 / 1.29 or 2.0 bits/s. This differs from the slope reciprocal bandwidth by a factor of five! This is a concern if one wishes to generalize findings in terms of the human rate of information processing. Is the rate in this case 10.4 bits/s or 2.0 bits/s? As evident in Table 2, the regression line equations (and resulting bandwidths) vary tremendously in previous Fitts' law research using the mouse in point-select tasks.
A third possibility for calculating the prediction model is regression-through-the-origin. Although it has never been employed, the method will produce the best-fitting line passing through the origin.
Since linear regression produces the prediction line with the best fit, it is the preferred choice for model building. However, the proviso is added that the intercept must be small. "Small" in this context is on the order of a few hundred milliseconds — a value which can reasonably be attributed to random variation in measurements.
Prediction Equations and Bandwidths From Fitts' Law
Studies Using a Mouse in Point-Select Tasks
| Study | Prediction equation (ms) | Bandwidth (bits/s) |
|---|---|---|
| Boritz et al., 1991 | MT = 1320 + 430 ID | 2.3 |
| Epps, 1986 | MT = 108 + 392 ID | 2.6 |
| MacKenzie et al., 1990 | MT = −107 + 223 ID | 4.5 |
| Han et al., 1990 | MT = 389 + 175 ID | 5.7 |
| Card et al., 1978 | MT = 1030 + 96 ID | 10.4 |
| Gillan et al., 1990 | MT = 795 + 83 ID | 12.0 |
Refinements to Fitts' Law
Despite an extremely good fit in empirical tests, Fitts' law is a frequent target for critical reviews (e.g., Meyer, Smith, Kornblum, Abrams, & Wright, 1990; MacKenzie, in press; Welford, 1968). Numerous problems surface under close examination or when findings are compared across studies. These have motivated corrections or refinements to the model. In this section we review these and offer suggestions to guide researchers in applying the law.
Formulation for Index of Difficulty
Early examinations of the law noted a consistent departure of data points above the regression line for "easy" tasks (ID < 3 bits). A new formulation for ID was proposed by Welford (1960) to correct this:
| ID = log2(A / W + 0.5) | (6) |
Many researchers, including Fitts, noted an improved fit using Equation 6. The Welford formulation was used by Card et al. (1978), whose findings were subsequently elaborated in the Psychology of human-computer interaction (Card, Moran, & Newell, 1983). Not surprisingly, many HCI researchers citing Card and colleagues adopt the Welford formulation (e.g., Boritz et al., 1991; Gillan et al., 1990).
It has also been argued that Fitts, in formulating his model, deviated unnecessarily from Shannon's original work in information theory (MacKenzie, 1989; Shannon & Weaver, 1949), and that a more theoretically sound formulation for the index of task difficulty is
| ID = log2(A / W + 1) | (7) |
In terms of MT, the prediction model becomes
| MT = a + b log2(A / W + 1) | (8) |
Equation 8, known as the Shannon formulation, is preferred because it
- provides a slightly better fit with observations,
- exactly mimics the information theorem underlying Fitts' law, and
- always gives a positive rating for the index of task difficulty.
The last point above is understood by examining the three formulations for ID. Using the Fitts or Welford formulation (Equations 1 & 6), the index is negative if the amplitude is less than half the target width; that is, A < W / 2. At the very least, a negative rating for task difficulty is a nuisance. From Equation 7, as A approaches zero (for any W), ID approaches 0 bits, but never becomes negative. Obviously, the latter effect has strong intuitive appeal. Although for the one-dimensional paradigm an amplitude less than W / 2 only occurs when the starting position is inside the target (see Figure 2), very small A:W ratios are fully possible when the law is applied in two dimensional tasks. This is demonstrated in the next section.
Extension to Two Dimensions
It is important to remember that the experiments undertaken by Fitts and most other experimental psychologists tested one dimensional movements. This is evident in Figures 1 and 2. Since both target amplitude and target width are measured along the same axis, it follows that the model is inherently one dimensional.
HCI researchers employing Fitts' law invariably use target selection tasks realized on a two-dimensional CRT display. The shape of the target and the angle of approach, therefore, must be considered carefully in applying the model. If the targets are circles (or perhaps squares), then the one-dimensional constraint remains largely intact. (The "width" of a circle is the same, regardless of the angle of measurement!) However, if targets are rectangles (e.g., "words"), the situation is confounded. We can still view the amplitude as the distance to the centre of the target; but the definition of target width is unclear. This is illustrated in Figure 5.
In applying the model in 2D tasks, a critical question arises: What is target width? The default strategy is to consistently use the horizontal extent of the target. We call this the "STATUS QUO" model for target width. Unfortunately, a STATUS QUO model yields unrealistically low (sometimes negative!) estimates for task difficulty when, for example, a short and wide target, such as a word or series of words, is approached from above or below at close range. At least two examples of this exist in the literature. Gillan et al. (1990) used Fitts' law in a target selection task using strings of characters as targets while varying the approach angle and approach distance. One extreme condition saw a 26-character (6 cm) target approached diagonally from a distance of 2 cm. Welford's formulation was used, so the index of task difficulty was ID = log2(A / W + 0.5) = log2(2 / 6 + 0.5) = −2.6 bits. The negative rating is troublesome. (A similar example is found in Card et al., 1978).
One result of task difficulty extending to the left of ID = 0 bits is that it becomes certain that a positive (probably large) intercept emerges under linear regression. This is because conditions with ID = 0 bits or less correspond to conditions that actually occurred in the experiment. No doubt, such tasks will take a non-trivial (positive) amount of time.
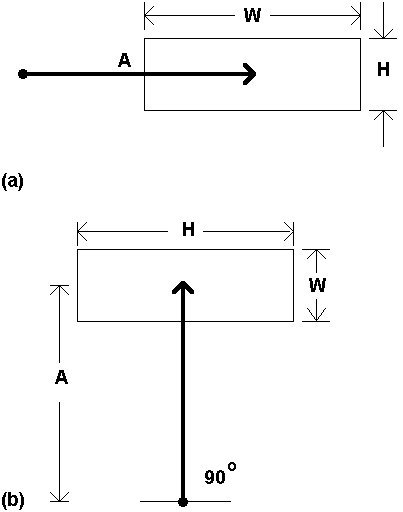
Figure 5. Fitts' law in two dimensions. The roles of width and height
reverse as the approach angle changes from 0° to 90°.
We suggest two ways to correct this problem. The first is to use the Shannon formulation for ID, which for the example above would increase the rating to log2(2 / 6 + 1) = +0.42 bits.
A second and additional strategy is to substitute for W a measure more consistent with the 2D nature of the task. Consider Figure 6. The inherent 1D constraint in the model is maintained by measuring W along the approach axis. This is shown as W' (read "W prime") in the figure. Notwithstanding the assertion that subjects may "cut corners" to minimize distances, the W' model is appealing because it allows a 1D interpretation of a 2D task.
Another possible substitution for target width is "the smaller of W or H". This pragmatic approach has intuitive appeal in that the smaller of the two dimensions seems more indicative of the accuracy demands of the task. We call this the "SMALLER-OF" model. This model is computationally simple since it can be applied only knowing A, W, and H. The W' model, on the other hand, requires A, W, H, and QA, and a geometric calculation to determine the correct substitution for W. The SMALLER-OF model is limited to rectangular targets, however.
An experiment was conducted to test the different models for target width on a standard target selection task using a mouse. The design employed a balanced range of short-and-wide and tall-and-narrow targets approached from various angles. The results indicate that both the SMALLER-OF and W' models are empirically superior to the STATUS QUO model and that the difference between the SMALLER-OF and W' models is insignificant (MacKenzie & Buxton, in press).
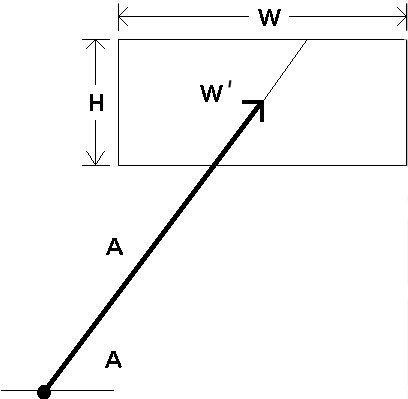
Figure 6. What is target width? Possibilities include W '
(the width of the target along an approach vector) or the smaller
of W or H.
In summary, the SMALLER-OF or W' model is recommended in applying Fitts' law to two dimensional tasks. We should note that extensions to three dimensional tasks easily follow from the arguments above; although Fitts' law has yet to be tested in 3-space. Finally, note that the W ' model reduces to the STATUS QUO model for one dimensional tasks.
Normalization and the Speed-Accuracy Tradeoff
The reciprocity between the speed of actions and the subsequent accuracy of responses has been well documented in experimental psychology and human factors engineering (e.g., Hancock & Newell, 1985; Pew, 1969). Despite this, researchers all too often base performance analyses solely or largely on task completion time measurements while paying little regard to the errors that accompanied — and equally contributed to — performance. Comparative evaluations based on movement time criteria are difficult when faced with disparities in error rates. That is, if condition A was faster than condition B, but had more errors, it is uncertain which condition is better.
The most important refinement to Fitts' law, perhaps, is the technique for accommodating spatial variability or errors in responses. The techniques calls for target width to be adjusted based on the distribution of "hits" (selection coordinates) about each target. Thus, at the model building stage, W is a dependent variable rather than an independent variable. The claim is that the technique increases the power of Fitts' law since normalized models inherit a known and consistent error rate. In particular, comparisons within and between studies are strengthened by a "level playing field".
The output or "effective" target width (We ) is derived from the observed distribution of "hits", as described by Crossman and Welford (Welford, 1968, p. 147). This adjustment lies at the very heart of the information-theoretic metaphor — that movement amplitudes are analogous to "signals" and that end-point variability (viz., target width) is analogous to "noise".
The technique is illustrated in Figure 7. When a nominal error rate of 4% occurs (Figure 7a), no adjustment is required (We = W). When a different error rate occurs, target width is adjusted by multiplying it by a ratio of z scores obtained from statistical tables for the unit-normal curve. For example, if 2% errors were recorded on a block of trials when selecting a 5 cm wide target, then We = 2.066 / 2.326 × 5 = 4.45 cm (Figure 7b).1 The analyses proceed as before except using "effective IDs", calculated using We instead of W.
Applying this technique is essential if comparisons within or across studies are attempted. Rephrasing and earlier point, if performance on condition A was 6 bits/s and performance on condition B was 5 bits/s, we'd like to conclude that condition A was superior; however, in the absence of identical or normalized error rates, such a conclusion is weak and perhaps wrong. Fitts' law models have appeared in published research accompanied by error rates from 0% to 25% (see MacKenzie, in press); yet the technique is rarely applied. It is strongly recommended that future research adopt the method.
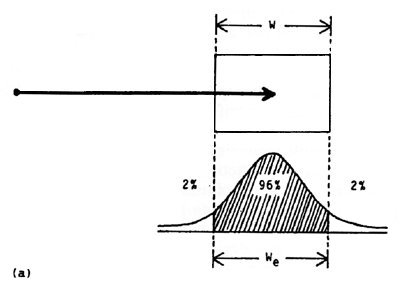
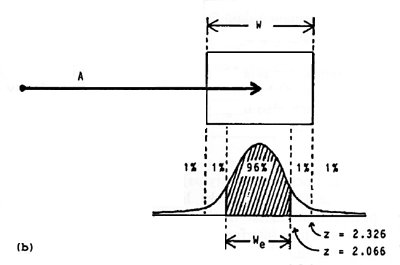
Figure 7. The method for normalizing responses. In (a) the error rate
is 4% so no adjustment is needed. In (b) the rate is 2% so an adjustment is made.
Applying Fitts' Law: An Example
One challenge in research is relating the findings to real-world problems confronting practitioners in the field. Despite its recognition as one of the more robust models for human movement, Fitts' law has rarely migrated from the research lab.An instance of Fitts' law actually being used in a product is a computer-aided design tool called Jack, developed at the University of Pennsylvania (Badler, Webber, & Kalita, 1991). In Jack three dimensional human figures (simulated on a CRT display) are programmed to execute motions such a picking up objects or making adjustments on a simulated control panel. Since the researchers did not know how fast to program movements in Jack, they called upon Fitts' law. A derived Fitts' law model was embedded in Jack to provide the duration for movements, based on the distance to move and the size of the terminating region for the move. The visual result is quite natural.
In this section, further applications for Fitts' law models are explored and a specific example is developed.
First, we must recognize when not to use Fitts' law. The law is a prediction model for rapid, aimed movement. A variety of user input activities do not fit this description, including drawing, inking, writing cursive script, and other temporarily constrained tasks. Furthermore, some devices are inadequately modeled by Fitts' law. Isometric joysticks are force sensing and undergo negligible motion. As a model for human movement, it seems odd to apply Fitts' law where no limb movement takes place. Card et al. (1978) found that performance data for an isometric joystick were poorly described by Fitts' law. After the data were decomposed by amplitude, however, the model fit well, yielding a series of parallel lines across amplitude conditions. Other devices, such as those for velocity control, may also display characteristics inappropriate for a Fitts' law model.
For the more common pointing devices (such as the mouse, trackball, or stylus), and for common point-select or drag-select tasks, however, Fitts' law has the potential to assist in the design and evaluation of graphical user interfaces. Questions of the form "How long will this task take?" can be answered using Fitts' law prediction equations if certain conditions exist. If the tasks are rapidly executed with negligible or known mental preparation time, system response time, device homing time, etc., then there is a good chance Fitts' law can assist in evaluating alternative methods.
Consider the case of deleting a file (icon) on the Apple Macintosh computer. Three possible methods are listed below.
DRAG-SELECT: Drag the icon to the trashcan. (This is the traditional Macintosh method.)
POINT-SELECT: Select the file icon with a point-select operation, then select the trashcan icon with a second point-select operation.
STROKE-THROUGH: Stroke through the icon. This method uses a button-down action beside the file icon followed by dragging (stroking) through the icon and a button-up action on the opposite side.
The STROKE-THROUGH method is an example of input which mimics a natural gesture in manuscript editing (Hardock, 1991; Kurtenbach & Buxton, 1991). A reasonable assumption for the stroking gesture is that the button-down action occurs on the left of the icon in the centre of a region the same size as the icon, and that the button-up action occurs similarly in a region on the right of the icon.
A possible screen layout is shown in Figure 8. The trashcan icon is located at the bottom right of the screen. The file icon is placed in the middle of the screen at a distance of 14 cm from the trashcan. Both icons are 2 cm square. The button-down and button-up regions for the stroking gesture are shown in dotted lines.
The calculations proceed using derived pointing and dragging models for the mouse (MacKenzie et al., 1991):
Pointing model:
| MT = 230 + 166 × ID (IP = 6.0 bits/s) | (9) |
Dragging model:
| MT = 135 + 249 × ID (IP = 4.0 bits/s) | (10) |
The pointing model applies to the POINT-SELECT method, while the dragging model applies to the DRAG-SELECT and STROKE-THROUGH methods. Note also that for the STROKE-THROUGH method the amplitude is 4 cm, rather than 14 cm.
Once the initial move to the icon is complete, the time to delete the file icon using each method is calculated as follows:
DRAG-SELECT:
| MT = 135 + 249 log2(14 / 2 + 1) = 135 + 249 × 3 = 882 ms | (11) |
POINT-SELECT:
| MT = 230 + 166 log2(14 / 2 + 1) = 230 + 166 × 3 = 728 ms | (12) |
STROKE-THROUGH:
| MT = 135 + 249 log2(4 / 2 + 1) = 135 + 249 × 1.58 = 528 ms | (13) |
This result suggests, using Fitts' law analyses, that the traditional method of deleting a file on the Macintosh is slower than two alternate methods. (The STROKE-THROUGH method is 40% faster.) The example is simplistic, however. Other issues such as methods for deleting multiple files or for un-deleting files must be considered too.
Even though the rate of information processing is lower during dragging than during pointing, the STROKE-THROUGH method, which is a dragging operation, is faster than the POINT-SELECT method. This is due to the combined effect of the intercepts in the prediction equations and the different movement amplitudes. Using the stroke-through method, the predicted MT is independent of the distance (A) between the file icon and the trashcan icon since the movement amplitude is nominally set at twice the file icon's width. However, the predicted MT decreases with A for the POINT-SELECT method. This suggests there may be a cross-over point below which the POINT-SELECT method is faster. Knowledge of this may play a critical role in selecting an appropriate method. In the current example, the cross-over point is calculated by equating the POINT-SELECT and STROKE-THROUGH predictions as follows:
| 230 + 166 × log2(A / 2 + 1) = 135 + 249 × log2(A / 2 + 1) | (14) |
Solving Equation 14 yields A = 2.72 cm. So, the point-select method is faster than the STROKE-THROUGH method only for amplitudes less than 2.72 cm. Certainly, this is a minority of cases. Other possibilities could be explored too, such as increasing the size of the trashcan icon relative to file icons.
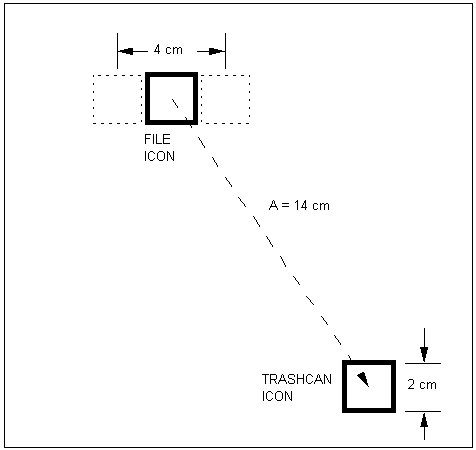
Figure 8. Screen layout for Fitts' law example.
Future Possibilities
In the hard science-soft science debate, Newell and Card (1985) hold that "striving to develop a theory that does task analysis by calculation is the key to hardening the science" (p. 237). Indeed, future applications of Fitts' law may include "embedded models" as an integral part of user interface design and management systems. The scenario envisioned goes something like this: A user interface is patched together in story-board fashion with a series of screens (with their associated soft buttons, pull-down menus, icons, etc.) and interconnecting links. The designer puts the embedded model into "analyse mode" and "works" the interface — positioning, drawing, selecting, and "doing" a series of typical operations. When finished, the embedded model furnishes a predicted minimum performance time for the tasks (coincident with a nominal or programmable error rate). The designer moves, changes, or scales objects and screens and requests a reanalysis of the same task.This is a rough first approximation. At a higher level, an embedded model is an "agent" in beta testing, monitoring activities and profiling performance. The profile catalogs a variety of facets of the interface. For example, a "locus of control" could identify frequently used screens or high-use regions on a display. In a word processing system, for example, depending on the implementation for scrolling, a user may work mostly at the bottom of the screen. Knowledge of this may imply that a menu bar could be placed at the bottom of the display rather than at the top.
A more powerful embedded model performs sequence analysis. How long does it take to get from point A to point B through a series of intermediate steps? Or, of alternate ways, which is the fastest? Hypermedia environments with embedded links facilitate such analyses, since an explicit and external state-transition description may not be needed. The agent acts on the screen definitions and links (as they exist in the application) in evaluating alternative or optimal paths.
An embedded model is more than a software routine incorporating Fitts' law. System and user performance constants are needed, similar to those in the Keystroke-Level Model (Card, Moran, & Newell, 1980). A parametric analysis could identify bottlenecks or optimal combinations. For example, decreasing pointing time by 10% vs. decreasing user keystroke time by 10% may have vastly different effects on overall task completion time. If a task can be accomplished two ways (e.g., 4 point-select operations vs. 20 keystrokes), which is the fastest? A parametric analysis could identify cross-over points across settings (as shown earlier). The designer could establish ranges and weights for parameters, and an agent, armed with embedded models, would take it from there.
Fitts' law may also participate in user-adaptive systems — systems with a human interface which changes to accommodate a user's capabilities and limitations (Rouse, 1988). Control systems for air traffic, ground traffic, power generation or industrial processes are potential instances. One can imagine several human operators interacting with a complex system by manipulating iconic controls in response to system events. As system dynamics change, the demands on operators change. Models such as Fitts' law (and/or the Hick-Hyman law) could measure the load on operators (in bits/s) or predict their performance. In safety-critical settings, it may be possible to systematically allocate tasks to workers to maintain set-points of sub-maximal performance.
Human-computer interaction has advanced by leaps and bounds in recent years. We can attribute this primarily to the improved interfaces advanced through the technologies of mouse input and bit-mapped graphic output. There is an ongoing and valuable need for the prediction and modelling of user activities within such environments. As human-machine dialogues evolve and become more "direct", the processes and limitations underlying our ability to execute rapid, precise movements emerge as performance determinants in interactive systems. Powerful models such as Fitts' law can provide vital insight into strategies for optimizing performance in a diverse design space.
Acknowledgement
This paper is based on research conducted at the Computer Systems Research Institute in the University of Toronto. The financial support of the Natural Sciences and Engineering Research Council of Canada, Xerox Palo Alto Research Center, and Digital Equipment Corp. is gratefully acknowledged.
References
Badler, N. I., Webber, B. L., & Kalita, J. (1991). Animation from instructions. In N. I. Badler, B. A. Barsky, & D. Zeltzer (Eds.), Making them move: Mechanics, control, and animation of articulated figures (pp. 51-93). San Mateo, CA: Morgan KaufmannBoritz, J., Booth, K. S., & Cowan, W. B. (1991). Fitts's law studies of directional mouse movement. Proceedings of Graphics Interface `91 (pp. 216-223). Toronto: CIPS.
Card, S. K., English, W. K., & Burr, B. J. (1978). Evaluation of mouse, rate-controlled isometric joystick, step keys, and text keys for text selection on a CRT. Ergonomics, 21, 601-613.
Card, S. K., Mackinlay, J. D., & Robertson, G. G. (1990). The design space of input devices. Proceedings of the CHI `90 Conference on Human Factors in Computing Systems (pp. 117-124). New York: ACM.
Card, S. K., Moran, T. P., & Newell, A. (1980). Psychology of human-computer interaction. Hillsdale, NJ: Erlbaum.
Epps, B. W. (1986). Comparison of six cursor control devices based on Fitts' law models. Proceedings of the 30th Annual Meeting of the Human Factors Society (pp. 327-331). Santa Monica, CA: Human Factors Society.
Fitts, P. M. (1954). The information capacity of the human motor system in controlling the amplitude of movement. Journal of Experimental Psychology, 47, 381-391.
Fitts, P. M., & Peterson, J. R. (1964). Information capacity of discrete motor responses. Journal of Experimental Psychology, 67, 103-112.
Gillan, D. J., Holden, K., Adam, S., Rudisill, M., & Magee, L. (1990). How does Fitts' law fit pointing and dragging? Proceedings of the CHI '90 Conference on Human Factors in Computing Systems (pp. 227-234). New York: ACM.
Han, S. H., Jorna, G. C., Miller, R. H., & Tan, K. C. (1990). A comparison of four input devices for the Macintosh interface. Proceedings of the 34th Annual Meeting of the Human Factors Society (pp. 267-271). Santa Monica, CA: Human Factors Society.
Hancock, P. A., & Newell, K. M. (1985). The movement speed-accuracy relationship in space-time. In H. Heuer, U. Kleinbeck, & K.-H. Schmidt (Eds.), Motor behavior: Programming, control, and acquisition (pp. 153-188). New York: Springer-Verlag.
Hardock, G. (1991). Design issues for line-driven text editing/annotation systems. Proceedings of Graphics Interface `91 (pp. 77-84). Toronto: CIPS.
Hick, W. E. (1952). On the rate of gain of information. Quarterly Journal of Experimental Psychology, 4, 11-26.
Hyman, R. (1953). Stimulus information as a determinant of reaction time. Journal of Experimental Psychology, 45, 188-196.
Kurtenbach, G., & Buxton, W. (1991). GEdit: A testbed for editing by contiguous gesture. SIGCHI Bulletin, 32(2), 22-26.
MacKenzie, I. S. (1989). A note on the information-theoretic basis for Fitts' law. Journal of Motor Behavior, 21, 323-330.
MacKenzie, I. S. (1991). Fitts' law as a performance model for
human-computer interaction. Doctoral dissertation. University of Toronto.
MacKenzie, I. S. (in press). Fitts' law as a research and design tool in
human-computer interaction. Human-Computer Interaction.
MacKenzie, I. S., & Buxton, W. (in press). Extending Fitts' law to two dimensional tasks. Proceedings of the CHI `92 Conference on Human Factors in Computing Systems. New York: ACM.
MacKenzie, I. S., Sellen, A., & Buxton, W. (1991). A comparison of input devices in elemental pointing and dragging tasks. Proceedings of the CHI '91 Conference on Human Factors in Computing Systems (pp. 161-166). New York: ACM.
Meyer, D. E., Smith, J. E. K., Kornblum, S., Abrams, R. A., & Wright, C. E. (1990). Speed-accuracy tradeoffs in aimed movements: Toward a theory of rapid voluntary action. In M. Jeannerod (Ed.), Attention and performance XIII (pp. 173-226). Hillsdale, NJ: Erlbaum.
Miller, G. A. (1953). What is information measurement? American Psychologist, 8, 3-11.
Newell, A., & Card, S. K. (1985). The prospects for psychological science in human-computer interaction. Human-Computer Interaction, 1, 209-242.
Pew, R. W. (1969). The speed-accuracy operating characteristic. Acta Psychologica, 30, 16-26.
Rouse, W. B. (1988). Adaptive aiding for human/computer control. Human Factors, 30, 431-443.
Shannon, C. E., & Weaver, W. (1949). The mathematical theory of communication. Urbana, IL: University of Illinois Press.
Walker, N., & Smelcer, J. B. (1990). A comparison of selection times from walking and pull-down menus. Proceedings of the CHI `90 Conference on Human Factors in Computing Systems (pp. 221-225). New York: ACM.
Ware, C., & Mikaelian, H. H. (1989). A evaluation of an eye tracker as a device for computer input. Proceedings of the CHI+GI '87 Conference on Human Factors in Computing Systems and Graphics Interface (pp. 183-188). New York: ACM.
Welford, A. T. (1960). The measurement of sensory-motor performance: Survey and reappraisal of twelve years' progress. Ergonomics, 3, 189-230.
Welford, A. T. (1968). Fundamentals of skill. London: Methuen.
-----
Footnotes:
1 The technique is described elsewhere in full detail with examples (MacKenzie, in press).