Akamatsu, M., & MacKenzie, I. S. (1996). Movement characteristics using a mouse with tactile and force feedback. International Journal of Human-Computer Studies, 45, 483-493. [software]

Movement Characteristics Using a Mouse With Tactile and Force Feedback

Motoyuki Akamatsu1 & I. Scott MacKenzie2

1National Institute of Bioscience and Human Technology
AIST, MITI, Japan

2Dept. of Computing and Information Science
University of Guelph
Guelph, Ontario, Canada N1G 2W1

Abstract
A multi-modal mouse incorporating tactile and force feedback was tested in a target selection task with twelve subjects. Four feedback conditions (normal, tactile, force, tactile+force) were combined with three target distances and three target sizes. We found significant reductions in the overall movement times and in the time to stop the cursor after entering the target. This effect was particularly pronounced for the tactile condition and for small targets. However, compared to normal feedback, error rates were higher with the tactile and tactile+force conditions. The motor-sensory bandwidth calculated using Fitts' law, normalized for spatial variability, was highest in the presence of tactile feedback (6.4 bits/s). This was followed by tactile+force (6.2 bits/s), normal (5.9 bits/s), and force feedback (5.8 bits/s). These results indicate that modifying a mouse to include tactile feedback, and to a lesser extent, force feedback, offers performance advantages in target selection tasks.

Keywords: Tactile feedback, force feedback, pointing devices, Fitts' law, sensory feedback, modalities, human-computer interfaces

1. Introduction

Although once used only for batch data processing, computer systems are now a critical tool in many applications. Genres such as multi media, virtual reality, computer games, as well as traditional fields such as industrial control and aviation have evolved and changed dramatically as computer technology enters the picture.

Improving the human-computer interface is now considered critical for user acceptance of new systems, and for ensuring that work environments are safe, comfortable, and efficient. A recent focus in human-computer interfaces is in exploring new and appropriate sensory modalities of interaction (Baecker, Grudin, Buxton & Greenberg, 1995; Chap. 7). The use of the visual and auditory channels are the most obvious examples; but improving the dynamics of movement through kinesthetic and other forms of feedback is also important. Most movements engage the sensation of touch or force, so it seems reasonable to exploit these at the human-computer interface.

In this paper, we present the results of an empirical study that investigates the movement characteristics of a multi-modal mouse -- a mouse that includes tactile and force feedback. Our experiment used a simple target selection task while varying the target distance, target size, and the sensory modality. The use of a "normal" display served as a base-line condition, and to this we added tactile, force, and tactile+force as additional conditions. We are interested in understanding how the different feedback modalities affect the dynamics of movements. These include not only the speed and accuracy of responses, but also the effects of tactile and force feedback on the microstructure of movements (i.e., entering a target region or completing a selection).

The work presented here is a follow-up to earlier work (Akamatsu and Sato 1994). Our previous experiment was a 2 × 2 factorial design which varied target distance (2 levels) and feedback modality (2 levels). Our feedback conditions were "normal" and multi-modal, the latter incorporating both tactile and force feedback. The present experiment provides a more complete set of movement tasks (3 sizes × 3 distances), and four feedback conditions (normal, tactile, force, and tactile+force). This design affords a more thorough examination of the effects of tactile and force feedback on the characteristics of target selection.

2. The Multi-Modal Mouse

Since its invention in the 1960s (English, Engelbart & Berman, 1967), the mouse has evolved to become the dominant pointing and selecting device for desktop computers. Commercialization began in 1981 with the Xerox Star (Johnson et al., 1989); but wide public acceptance did not occur until 1983 when the Apple Macintosh was introduced (Perry & Voelcker, 1989). With a ball underneath and one to three buttons on top, the design of the mouse has remained remarkably stable over the years.

In conventional usage, a mouse interface provides proprioceptive feedback through grasping and visual feedback via the stimulus presented on the computer system's display. Our multi-modal mouse provides additional, more direct feedback by delivering tactile and/or force stimulus directly to the hand and finger tip. This comes by way of (a) a solenoid-driven pin that stimulates the index finger resting on the mouse button (tactile feedback), and (b) an electromagnet in the mouse chassis that, while energized, creates drag between the mouse and an iron mousepad (force feedback). A detailed description of the design of our multi-modal mouse is provided by Akamatsu and Sato (1994).

3. Tactile and Force Feedback

The use of tactile or force feedback in computer interfaces is not new. Not surprisingly, systems with tactile feedback, called tactile displays, have been developed as a sensory replacement channel for handicapped users. An early example is the Optacon, a sensory aid for the blind developed by Bliss and colleagues (Bliss et al., 1970). This tactile reading aid, which is still in use, consists of 144 piezoelectric bimorph pins in a 24-by-6 matrix.

In a 2D application called Sandpaper, Minsky et al. (1990) added mechanical actuators to a joystick and programmed them to behave as virtual springs. When the cursor was positioned over different grades of virtual sandpaper, the springs pulled the user's hand toward low regions and away from high regions. In an empirical test without visual feedback, users could reliably order different grades of sandpaper by granularity. We created a similar test with our multi-modal mouse and confirmed their results (Akamatsu, Sato & MacKenzie, 1995).

Some of the most exciting work explores tactile feedback in 3D interfaces. Virtual reality input gloves are inherently a gesture technology because they operate in a feedback void. Imagine the task of tying virtual shoelaces. Without the sense of force or touch, this task is formidable: The virtual hand passes through the laces without any sense of the presence of the laces or shoes. This problem has inspired substantial research into new 3D input technologies. An early effort by Zimmerman, Lanier, Blanchard, Bryon, and Harvill (1987) was to modify a VPL DataGlove by mounting piezoceramic benders under each finger. When the virtual fingertips touched the surface of a virtual object, contact was cued by a "tingling" feeling created by transmitting a 20-40 Hz sine wave through the piezoceramic transducers. This is a potential solution to the blind touch problem; however, providing appropriate feedback when a virtual hand contacts a virtual hard surface is extremely difficult. Brooks, Ouh-Young, Batter and Kilpatrick (1990) confronted the same problem and noted that systems with inertia and velocity must be critically damped. The challenge is to avoid oscillations or a mushy feeling upon contact.

Force feedback has also been implemented in computer input devices. Engel, Goossens and Haakma (1992) describe a trackball with corrective force feedback to "guide" the user toward preferred cursor positions. Iwata (1990) described a six degree-of-freedom mechanical manipulator with force feedback. When a hard surface is contacted in the virtual workspace, the manipulator is locked and the user feels the surface as resistance to movement in the control.

One potential benefit in adding force and tactile feedback is that the processing demands of the visual channel are diminished, freeing up capacity for other purposes. Such a payoff has been predicted before (Card, Mackinlay & Robertson, 1991), but the deliverables remain outstanding.

4. Method

4.1. SUBJECTS

Twelve volunteer subjects participated in the experiment. The subjects were 11 male and 1 female, ranging in age from 29 to 44. All subjects were regular users of mice in their daily work.

4.2. APPARATUS

The experiment was conducted using the multi-modal mouse described earlier. The host computer was a PC-compatible NEC model PC9801. A second PC9801 was used for data collection to capture mouse coordinates and button activity to 1 pixel and 1 ms resolution. The data were saved in output files for subsequent analysis. Subjects sat in a special isolation room while the experimenter sat in an adjoining room.

4.3. PROCEDURE

Subjects performed a simple target selection task. The experimental screen consisted of a start circle in the lower left of the display and a square target in the upper right of the display. All movements were up and to the right at an angle of 56 degrees from horizontal. At the beginning of each trial, the subject moved the cursor into the start circle. After a random time interval the circle disappeared, signaling the beginning of the trial.

Subjects were instructed to move the cursor as quickly and accurately as possible to the target and select the target by pressing the left mouse button.

4.4. DESIGN

The experiment was a 3 × 3 × 4 fully within-subjects repeated measures design. The factors and levels were as follows:

Target Distance72, 144, 288 pixels
Target Size11, 21, 41 pixels
Feedbacknormal, tactile, force, tactile+force

The target distance and size conditions use factor-of-two increments. An additional pixel was added for target size for convenience to create a centre point for the target. These conditions create a range of task difficulties typical of point-select tasks. One common metric for task difficulty is Fitts' index of difficulty (ID) in bits (Fitts 1954). In the present experiment, we use the Shannon formulation (MacKenzie 1992), as follows:

ID = log2(A / W + 1) (1)

where A is the target distance, or amplitude, and W is the target size, or width. Using Equation 1, the tasks ranged from

ID = log2(72 / 41 + 1) = 1.5 bits (2)

for the easiest task, to

ID = log2(288 / 11 + 1) = 4.8 bits (3)

for the hardest task.

For the normal feedback condition, target entry was indicated only through the displayed image of the cursor's path. No additional feedback was provided.

For the tactile condition, the solenoid driving the pin inside the mouse was energized while the cursor was inside the target boundary. This resulted in a persistent sensation, reminding the subject that the cursor is "on-target".

For the force condition, the electromagnet was energized with a 10 VDC signal while the cursor was inside the target. This increased the drag in the mouse by 0.1 N, representing an increase of 12-13% over the normal condition.

The tactile+force condition combined the stimuli described above for the tactile and force conditions.

Each subject participated in three groups of four sessions. Each group consisted of one session for each feedback condition. The first group (four sessions) served to familiarize the subjects with the experiment. Only the data from the second and third groups (eight sessions) were analyzed.

To counterbalance for learning effects, all 24 possible orders of the four feedback conditions were used. Subjects were assigned randomly to two orders; they performed one order in the second group of sessions and one in the third group of sessions. In each session subjects received, in random order, six repetitions of each of the nine target distance and size conditions. Over the three groups of 12 sessions, therefore, each subject performed 54 × 36 = 1944 trials, of which 1296 were used in the data analysis.

Several dependent measurements were taken. The coordinates of selection and the time to complete each task were recorded. A trial began when the subject moved the cursor after the start circle disappeared. A trial ended on the first button-down action for selecting the target. Trials in which subjects missed the target were not excluded from the analyses.

We also defined two intermediate points: the time when the cursor entered the target, and the time when the cursor stopped. By thus decomposing each trial, we were able to analyze five dependent temporal measurements: movement time, approach time, selection time, stopping time, and clicking time. These are shown in Figure 1.


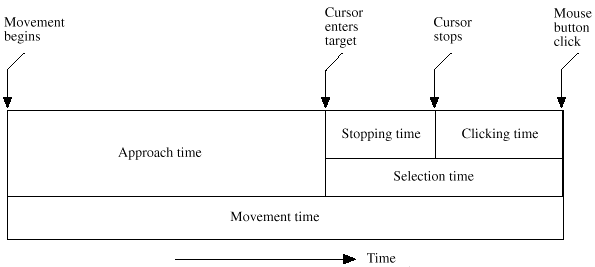
Figure 1. Time measurement for each trial. Movement time was
composed of an approach time and a selection time. Selection
time was composed of a stopping time and a clicking time.

An additional dependent measure was bandwidth (in bits/s), calculated by dividing the mean task difficulty (in bits) by the mean movement time (in seconds).

5. Results and Discussion

The effects of the four feedback modalities on the dependent measures of movement time, error rate, and bandwidth are summarized in Table 1. We will elaborate on and discuss these results in three parts: temporal analyses, spatial analyses, and Fitts' law models.

Table 1
Effects for four feedback modalities on
movement time, error rate, and bandwidth
                               Feedback(a)                                      
                   ---------------------------------------------                
Dependent    Mean  Normal    Tactile    Force      Tactile+Force    Significance
--------------------------------------------------------------------------------
Movement     503   520       491         521       481              F3,33 = 11.5
  time (ms)        -         (-5.6%)     (+0.2%)   (-7.6%)          p < 0.0001  
                                                                                
Error        8.0   6.6       10.9        5.8       8.6              F3,33 = 6.22
  rate (%)         -         (+65.2%)    (-12.1%)  (+30.3%)         p < 0.005   
                                                                                
Bandwidth    6.1   5.9       6.4         5.8       6.2              F3,33 = 2.92
  (bits/s)         -         (+8.5%)     (-1.7%)   (+5.1%)          p < 0.05    
--------------------------------------------------------------------------------
(a) values in parentheses are percent change relative to normal feedback







5.1.
TEMPORAL ANALYSES


The mean movement time for all trials was 503 ms.  There was a significant
main effect for feedback 
(F3,33 = 11.5, p < 0.0001).  The
conditions from fastest to slowest were tactile+force (481 ms), tactile (491
ms), normal (520 ms), and force (521 ms).

As typical in experiments such as this, the effects for target distance and
target size were highly significant 
(F2,11 = 696, p < 0.0001
and F2,11 = 526, p < 0.0001 respectively).  Our primary motive
in using nine target distance-size conditions, however, was to ensure that the
tasks covered the typical range of real-world conditions and to allow valid
Fitts' models to be built.  Although, in the case of target size, we also were
interested in interaction effects with feedback (see below).

The significant effect for feedback was entirely due to the dynamics of
movement after the cursor entered the target.  This claim is supported by the
lack of significance in the main effect of feedback on approach time
(F3,33 = 1.86, p > 0.05) -- the time before the cursor entered
the target.  This is fully expected because the four stimulus conditions differ
only after the cursor enters the target; the stimulus is identical
during the cursor's approach to the target.  And so, we focus the remaining
temporal analyses on the selection time, stopping time, and clicking
time.

The mean selection time was 156 ms.  Recall that selection time is
decomposed into stopping time and clicking time.  The means for the latter two
were 82 ms and 74 ms, respectively.  For all three dependent measures, there
was a significant main effect for feedback and a significant interaction effect
for feedback × size.  The F-statistics and significance levels are
summarized in Table 2.




Table 2

F-statistics and significance levels for

feedback and feedback × size effects on selection

time, stopping time, and clicking time






Dependent        Effect             Significance
--------------------------------------------------------------
Selection Time   Feedback           F3,33 = 12.1, p < 0.0001
                 Feedback × Size    F6,66 =  2.2, p < 0.05  
Stopping Time    Feedback           F3,33 = 13.3, p < 0.0001
                 Feedback × Size    F6,66 =  3.2, p < 0.01  
Clicking Time    Feedback           F3,33 = 16.0, p < 0.0001
                 Feedback × Size    F6,66 =  2.7, p < 0.05






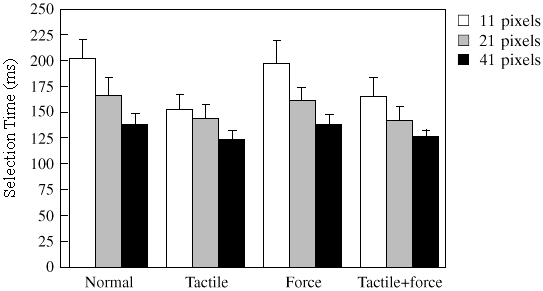
Figure 2 illustrates the effects for feedback and target size on selection
time, stopping time, and clicking time.  In Figure 2a, we see a clear
performance advantage for the tactile and tactile+force conditions over the
normal condition.  The effect is more pronounced for the smallest target for
the tactile condition.  The 11-pixel target took 203 ms to select with normal
feedback, but only 155 ms to select with tactile feedback.  This represents a
24% performance improvement.  The force and tactile+force conditions reveal
performance advantages, as well.  Scheffé post hoc comparisons revealed
that, with the small and medium-sized targets, the advantages were significant
with tactile and tactile+force feedback.  Comparisons among the large target
conditions were not significant.





(a)

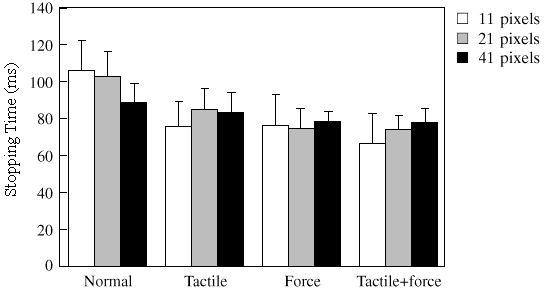
(b)

(c)

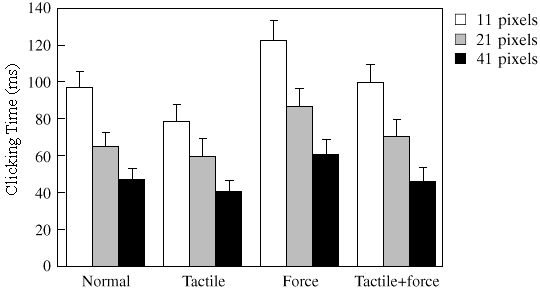
Figure 2.  The effect of feedback and target size on (a) selection time, 

(b) stopping time, and (c) clicking time.  Notes: (i) selection time = 

stopping time + clicking time, (ii) error bars represent 95%

confidence intervals.





Figure 2b shows the first portion of selection time: the stopping time.
Clearly, tactile, force, and tactile+force feedback decrease the stopping time
over the normal feedback condition.  The effect is more pronounced with the
smallest target, particularly with the tactile and tactile+force conditions.
This we attribute to the added and direct stimulus to the finger or hand of the
additional feedback modality.

In Figure 2c, however, we see the advantage disappear for the force and
tactile+force conditions due to longer clicking times.  This is possibly due to
subjects' compensating for the gain in stopping time by being less hurried in
selecting the target.  We feel, as well, that the acts of stopping the cursor
and selecting the target via a button push are separate, parallel motor-sensory
acts triggered by first-contact with the target.  Thus, a reduction in stopping
time will, in itself, cause an increase in clicking time. 

Tactile feedback appears to offer the best potential to reduce target
selection times, and this effect becomes more pronounced as targets get
smaller.


5.2.
SPATIAL ANALYSES


The mean error rate over all trials was 8.0%, as given in Table 1.  There
was a significant main effect for feedback 
(F3,33 = 6.22, p <
0.005).  The conditions from most accurate to least accurate were force (5.8%),
normal (6.6%), tactile+force (8.6%), and tactile (10.9%).  The speed advantage
of tactile feedback noted above is obviated by its poor showing in accuracy.
Furthermore, the poor showing was most pronounced for small targets -- the same
condition that yielded the best advantage for tactile feedback in the temporal
analysis.  The feedback × size interaction is statistically significant
(F6,66 = 4.6, p < 0.001); however, the differeces were
significant only among the small targets, as reveled in the post hoc test.
This is illustrated in Figure 3.






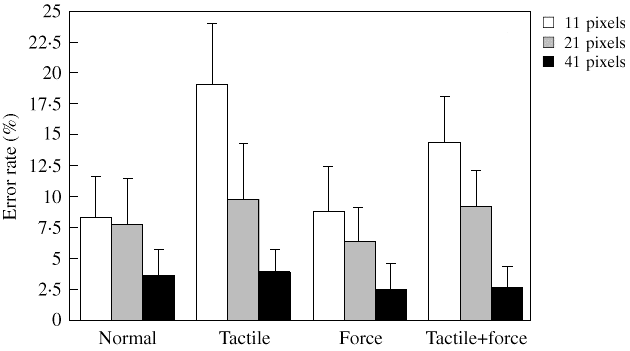
Figure 3.  The effect of feedback and target size on error 
rate.  The 11-pixel 
target was particularly difficult to 
select with the additional feedback modalities.




Although the 11-pixel target had an error rate of 8.3% with the normal
feedback, this rate more than doubled with tactile feedback, with an observed
rate of 19.0%.  However, when force feedback was also present, the error rate
dropped to 14.4%, and herein we see an advantage and an opportunity for
combining force feedback with tactile feedback.

The most accurate performance was observed with force feedback.  We
attribute this to the additional drag created by the electromagnetic.  This
will serve to maintain target position during the act of selecting the target
by pressing and releasing the mouse button.

The poor accuracy with tactile feedback may be explained as follows.  If
the cursor touches the edge of the target and then leaves the target, an error
may occur due to a reflexive muscle response; that is, the tactile stimulus of
entering the target triggers a muscle response that is difficult to reverse
(even though the cursor may have left the target).


5.3.
FITTS' LAW MODELS


If Fitts' index of difficulty , in bits (Equation 1), is divided by the
mean movement time, in seconds, then the result carries the units "bits per
second" (bits/s).  This measure is called the index of performance, or
bandwidth.  To accommodate spatial variability (i.e., errors), ID was
calculated as







     ID = log2(A / We + 1)

(4)





where A is the distance to the target and We is the
"effective target width".  The effective target width, We , is calculated
as 4.133 × SD, where SD is the standard deviation in spatial
coordinates, as described by Welford (1968).  By calculating We in this
manner, bandwidth as a dependent measure is strengthened because it emerges
from observations on the speed and accuracy of responses.  This is of
particular value when drawing comparisons between and within conditions because
the comparisons are based on a "level playing field".

The mean bandwidth for all conditions was 6.1 bits/s, as given in Table 1.
The main effect of feedback was statistically significant (F3,33 = 2.92,
p < 0.05).  From highest to lowest, the bandwidths across feedback
condition were 6.4% (tactile), 6.2% (tactile+force), 5.9% (normal), and 5.8%
(force).  These figures are within the range expected (see MacKenzie, 1992, for
a review of other studies using Fitts' law).  Even though responses with
tactile feedback were less accurate than with normal feedback, the bandwidth
was still higher by 8.5% in the former case.  The higher bandwidth with tactile
feedback implies that subjects are performing more efficiently with the added
feedback modality.  The combination of tactile and force feedback is less
advantageous, and force feedback alone yields slightly less efficient
performance than with normal feedback.

Besides bandwidth measurements, regression  models are usually presented to
verify that human motor-sensory tasks, under certain experimental conditions,
conform to Fitts' widely-used information-theoretic model.  The models for our
feedback conditions are given in Table 3.




Table 3

Fitts' law models for four feedback conditions






Feedback           Fitts' Law Model(a)      R2   
--------------------------------------------------
Normal             MT =  -67 + 195 ID       0.973
Tactile            MT =  -23 + 165 ID       0.960
Force              MT = -102 + 210 ID       0.977
Tactile+Force      MT =  -64 + 185 ID       0.971
--------------------------------------------------
(a) MT is movement time (ms), ID is index of     
    difficulty (bits), n = 9 and p < .0001 for   
    all models






Each model in Table 3 was calculated by regressing the nine target
distance-size conditions (IDs), calculated using Equation 4, on the
observed movement time (MT).  The slopes and intercepts in the models
are well within the range expected.  Noteworthy in Table 3 is the extremely
high R2; for all models, Fitts' model explains more than 96% of the
variance in observations.


Conclusion

This research tested a multi-modal mouse -- a mouse with tactile and force
feedback -- in a target selection that varied four feedback modalities with
target distance and target size.  Differences emerge between the feedback
modalities when the movements are examined after the cursor enters the target.
Both tactile and force feedback tend to reduce the stopping time -- the time
for the cursor to stop once it enters the target region.  Tactile feedback (but
not force feedback) also reduces the time to select a target after the cursor
stops.  Furthermore the effect is particularly pronounced for small
targets.

The benefits cited above are offset somewhat by higher error rates with
tactile and tactile+force feedback.  However, adding force feedback to tactile
feedback tends to reduce error rates with small targets.  Therefore an
opportunity exists to improve overall performance in a multi-modal mouse if
tactile feedback is used continuously and force feedback is turned on only when
the interface contains small targets.

Combining speed and accuracy in calculating Fitts' index of performance, or
bandwidth, reveals that tactile and tactile+force feedback are efficient
sensory modalities, being, respectively, about 8.5% and 5.1% more efficient
than normal feedback.  Although force feedback was the most accurate condition,
it was also the slowest and had the lowest bandwidth.

Although this research has shown effects for tactile and force feedback
when added to a mouse-type pointing device, a wider range of subjects and tasks
should be tested before applying this technology in the workplace.


Acknowledgment

We would like to thank the Natural Sciences and Engineering Research
Council (NSERC) in Canada for assistance in conducting this research.


References

AKAMATSU, M., MACKENZIE, I. S. & HASBROUCQ, T. (1995). A comparison of
tactile, auditory, and visual feedback in a pointing task using a mouse-type
device, Ergonomics, 38, 816-827.

AKAMATSU, M. & SATO, S. (1994). A multi-modal mouse with tactile and
force feedback, International Journal of Human-Computer Studies,
40, 443-453.

AKAMATSU, M., SATO, S. & MACKENZIE, I. S. (1994). Multimodal mouse: A
mouse-type device with tactile and force display, Presence, 3,
73-90.

BAECKER, R. M., GRUDIN, J., BUXTON, W. A. S.  & GREENBERG, S. (1995).
Readings in human-computer interaction: Toward the year 2000 [Chap. 7:
Touch, Gesture, and Marking]. San Francisco: Kaufmann.

BLISS, J. C., KATCHER, M. H., ROGERS, C. H. & SHEPPARD, R. P. (1970).
Optical-to-tactile image conversion for the blind, IEEE Transactions on
Man-Machine Systems, MMS-11, 58-65.

BROOKS, Jr., F. P., OUH-YOUNG, M., BATTER, J. J., & KILPATRICK, P. J.
(1990). Project GROPE: Haptic displays for scientific visualization.
Computer Graphics, 24(4), 177-185.

CARD, S. K., MACKINLAY, J. D. & ROBERTSON, G. G. (1991). A
morphological analysis of the design space in input devices. ACM
Transactions on Information Systems, 9, 99-122.

ENGEL, F. L., GOOSSENS, P. & HAAKMA, R. (1994). Improved efficiency
through I- and E-feedback: A trackball with contextual force feedback.
International Journal of Human-Computer Studies, 41,
949-974.

ENGLISH, W. K., ENGELBART, D. C. & BERMAN, M. L (1967). Display
selection techniques for text manipulation. IEEE Transactions on Human
Factors in Electronics, HFE-8, 21-31.

FITTS, P. M. (1954). The information capacity of the human motor system in
controlling the amplitude of movement. Journal of Experimental
Psychology, 47, 381-391.

IWATA, H. (1992). Artificial reality with force feedback: Development of
desktop virtual space with compact master manipulator. Computer
Graphics, 24, 165-170.

JOHNSON, J., ROBERTS, T. L., VERPLANK, W., SMITH, D. C., IRBY, C., BEARD,
M. & MACKEY, K. (1989). The Xerox Star: A retrospective, IEEE
Computer, 22(9), 11-29.

MACKENZIE, I. S. (1992). Fitts' law as a research and design tool for
human-computer interaction. Human-Computer Interaction, 7,
91-139.

MINSKY, M., OUH-YOUNG, M., STEELE, O., BROOKS, Jr., F. P., & BEHENSKY,
M. (1990). Feeling and seeing: Issues in force display, Computer
Graphics, 24, 235-275.

PERRY, T. S. & VOELCKER, J. (1989). Of mice and menus: Designing the
user-friendly interface. IEEE Spectrum, 26(9), 46-51.

WELFORD, A. T. (1968). The fundamentals of skill. London:
Methuen.

ZIMMERMAN, T. G., LANIER, J., BLANCHARD, C., BRYON, S., & HARVILL, Y.
(1987). A hand gesture interface devices. Proceedings of the CHI+GI
Conference on Human-Factors in Computing Systems, pp. 189-192. New York:
ACM.