Within-subjects vs. Between-subjects Designs: Which to Use?

I. Scott MacKenzie
Dept. of Computer Science
York University
Toronto, Ontario, Canada M3J 1P3
mack@cse.yorku.ca

 

Last update: 29/3/2013

 

The information in this research note appears in greater detail, and with additional discussion on experiment design, in Chapter 5 in Human-Computer Interaction: An Empirical Research Perspective (MacKenzie, 2013).

Background

Most empirical evaluations of input devices or interaction techniques are comparative.  A new device or technique is compared against alternative devices or techniques.  One design for such experiments is the within-subjects design, also known as a repeated-measures design.  In a within-subjects design, each participant is tested under each condition.  The conditions are, for example, "device A", "device B", etc.  So, for each participant, the measurements under one condition are repeated on the other conditions.  The alternative to a within-subjects design is a between-subjects design.  In this case, each participant is tested under one condition only.  One group of participants is tested under condition A, a separate group is tested under condition B, and so on.

The test conditions (A, B, ...) are levels of the same factor.  For example, the factor might be device and the levels might be mouse, trackball, and touchpad.  In experiments with more than one factor, it is possible to use a within-subjects (viz. repeated-measures) assignment for the levels of one factor and a between-subjects assignment for the levels of another factor.

Considerations for the Design of an Experiment

There are a number of issues to consider in deciding whether an experimental factor should be assigned within-subjects or between-subjects.

Sometimes there is no choice.  Here is an example where a between-subjects design must be used.  If hand preference is a factor in an experiment, it must be assigned between-subjects, because a participant cannot be both left handed and right handed!  Hand preference must be a between-subjects factor, with separate groups of left handers and right handers recruited for the experiment.

Conversely, here is an example where a within-subjects design must be used.  If an experiment seeks to investigate the acquisition of skill over multiple sessions of practice, then the only option for the factor session is within-subjects.  No two ways about it!  The factor is session, it is within-subjects, and the levels are session #1, session #2, session #3, and so on.

However, in many other situations, there is a choice.  If so, a within-subjects design is generally preferred.  There are at least two reasons.  First, fewer participants are needed in a within-subjects design since each participant is tested on all levels of a factor.  Although more testing is required for each participant, there is an advantage in having fewer participants overall, since recruiting, scheduling, briefing, demonstrating, practicing, and so on, are easier if there are fewer participants.

Another advantage of a within-subjects design is that there is less variance due to participant disposition (since there are fewer participants).  A participant who is predisposed to be meticulous (or reckless!) will likely exhibit such behaviour consistently across the experimental conditions.  This is beneficial because the variability in measurements is more likely due to differences among conditions than to behavioural differences between participants (if a between-subjects design were used).

Interference Effects and Learning Effects

Despite the above-noted advantages of a within-subjects design, a between-subjects design is sometimes preferred in order to avoid interference between the conditions.  If the conditions under test involve conflicting motor skills, such as typing on keyboards with different arrangements of keys, then a within-subjects design is a poor choice, because the required skill to operate one keyboard tends to inhibit, block, or otherwise interfere with, the skill required for the other keyboard.  Such a factor should be assigned between-subjects.

If interference is not anticipated, or if the effect is minimal and easily mitigated through a few minutes of practice when a participant changes conditions, then a within-subjects design should be considered.  However, one additional effect must be accounted for: learning.  Learning effects are due to the order of presentation.  They are in some sense the opposite of interference.  For example, if participants are tested under condition A first, then under condition B, they could potentially exhibit better performance under condition B simply due to prior practice under condition A.  To compensate for this, a technique known as counterbalancing is used.  Counterbalancing is performed by placing participants in groups and presenting conditions to each group in a different order.  The order is given by a Latin Square.

Latin Squares

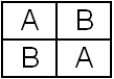
If the factor has two levels (e.g., A and B), participants are randomly assigned to groups of equal size: Group 1 is given condition A followed by condition B, while Group 2 is given condition B followed by condition A:

→ time

This is a trivial example of a Latin Square, known, in this case, as a 2 × 2 Latin Square.  If three or more conditions are tested, then a bit more planning is required.  Examples of 3 × 3, 4 × 4, and 5 × 5 Latin Squares follow:

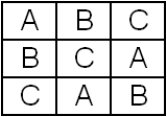
3 × 3 Latin Square

4 × 4 Latin Square

5 × 5 Latin Square

Look carefully, and the pattern is easily seen.  The defining characteristic of a Latin Square is that a condition appears precisely once in each row and in each column.  Because the order of presentation is different for each group of participants, the learning effect noted earlier tends to balance out. To ensure the groups are of equal size, the number of participants in the experiment should be a multiple of the number of conditions.  For example, 16 participants could be used in an experiment comparing 4 devices.  The participants are divided into four groups of four, and each group is assigned to one of the rows in the Latin Square.  There are different arrangements of conditions for Latin Squares of sizes 4 × 4 or larger.  An important variation is presented next.

Balanced Latin Squares

Counterbalancing conditions using a Latin Square does not fully eliminate the learning effect noted earlier.  Note in the 3 × 3 design that condition B follows condition A for two of the three groups of participants.  Similarly, in the 4 × 4 design, condition B follows condition A for three of the four groups of participants.  Thus, there is a tendency for better performance on condition B simply because most participants benefited from practice on condition A prior to testing on condition B.  This phenomenon is eliminated using a balanced Latin Square.  A 4 × 4 balanced Latin Square follows:

4 × 4 Balanced Latin Square

Note that each condition appears precisely once in each row and column, as before.  Furthermore, each condition appears before and after each other condition an equal number of times.  For example, condition B follows condition A two times and it also precedes condition A two times.  Thus, the imbalance noted earlier is eliminated.

Balanced Latin Squares do not exist for odd-order squares, such as 3 × 3, 5 × 5, etc.  However, it is possible to construct a balanced Latin square for any even number of conditions.  Here's the rubric: The 1st column is in order, starting at A.  The top row has the sequence, A, B, n, C, n - 1, D, n - 2, etc.  Entries in the 2nd and subsequent column are in order, with wrap around.  The 6 × 6 cases looks as follows:

6 × 6 Balanced Latin Square

In practice, within-subjects factors with more than four levels are rare in HCI experiments, so the 6 × 6 example is given just for curiosity.  For a good discussion on counterbalancing, see Martin (1996).

Did Counterbalancing Work?

When counterbalancing is used to assign levels of a within-subjects factor to participants, it is a good idea to verify that the desired effect was achieved – that learning was effectively canceled out (i.e., balanced).  This is verified by including "group" as a between-subjects factor in the analysis of variance.  The desired outcome is a non-significant "group effect".  This is typically what occurs.  However, sometimes the group effect is statistically significant.  The interpretation, in this case, is that counterbalancing did not work!  This is an unfortunate outcome.  The effect arises because of a particularly insidious form of leaning or interference known as asymmetric skill transfer (Poulton & Freeman, 1966).  In this case, there is not only a learning or interference effect, but the effect is different depending on the order of testing.  In other words, one condition tended to benefit or suffer more than others, depending on the preceding condition(s).  If there is any sense that asymmetrical skill transfer might occur, then it is best to assign the factor between-subjects. An example of asymmetric skill transfer from a published HCI paper is described in detail in Chapter 5 in the MacKenzie reference below.

References

MacKenzie, I. S. (2013). Human-computer interaction: An empirical research perspective. Waltham, MA: Morgan Kaufmann.

Martin, D. W. (1996). Doing psychology experiments. (4th ed.). Pacific Grove, CA: Brooks/Cole.

Poulton, E. C., & Freeman, P. R. (1966). Unwanted asymmetrical transfer effects with balanced experimental designs. Psychological Bulletin, 66(1-8).