MacKenzie, I. S., and Isokoski, P. (2008). Fitts' throughput and the speed-accuracy tradeoff. Proceedings of the ACM Conference on Human Factors in Computing Systems – CHI 2008, pp. 1633-1636. New York: ACM. [PDF] [software]
Fitts' Throughput and the Speed-Accuracy Tradeoff
I. Scott MacKenzie1 and Poika Isokoski2
1 Dept. of Computer Science and EngineeringYork University
Toronto, Canada M3J 1P3
mack@cse.yorku.ca
2
Department of Computer Sciences
University of Tampere
FIN-33014 University of Tampere, Finland
poika@cs.uta.fi
ABSTRACT
We describe an experiment to test the hypothesis that Fitts' throughput is independent of the speed-accuracy tradeoff. Eighteen participants used a mouse in performing a total of 5,400 target selection trials. Comparing nominal, speed-emphasis, and accuracy-emphasis conditions, significant main effects were found on movement time (ms) and error rate (%), but not on throughput (bits/s). In the latter case, failure to reject the null hypothesis of "no significant difference" (i.e., .05 < p < 1) is viewed as evidence supporting the constant-throughput hypothesis.Author Keywords
Fitts' law, throughput, speed-accuracy tradeoffACM Classification Keywords
H.5.2 User Interfaces. Input devices and strategies
INTRODUCTION
We explore an important but procedurally difficult tenet of Fitts' law: that throughput is independent of the speed-accuracy tradeoff (aka cognitive set). As space is limited, we direct readers to other sources for detailed discussions on Fitts' law and the utility of throughput [3-5].Additional work of note is Fitts and Radford's 1966 experiment, similar to ours, and with similar outcome. They report that "performance measured in information rate is almost identical in all cases for movements of intermediate difficulty executed under all three instructional sets for speed vs. accuracy." [1, p. 481] Their work was quite different, however: no computer apparatus was used, throughput values were not actually computed or reported, and an analysis of variance test for significant differences was not performed. Hence, the present work.
Throughput, Speed, and Accuracy
We now demonstrate the relationship between speed, accuracy, and throughput. Typically, speed is represented by the time to complete a task, usually known as movement time (MT) in Fitts' law experiments. One measure of accuracy is the percentage of trials where selection occurred outside the target. More information is available, however, if selection coordinates are recorded over a block of trials, and from these data the standard deviation in selection coordinates is computed. In view of the inherent one-dimensional nature of Fitts' law, we assume movement along the horizontal (x) axis, and use SDx as the measure of accuracy. Throughput (TP), in bits per second (bits/s), combines speed and accuracy in a single measure computed over repeated trials as follows:
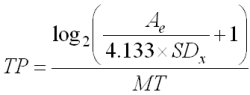
The numerator is the "effective index of difficulty" and includes Ae as the distance or amplitude of movements.
To explain the idea of constant throughput across cognitive sets, we use a hypothetical example. Assume participants perform a block of target selection trials under nominal conditions; i.e., proceeding quickly and accurately within their comfort zone. MTNOMINAL, SDNOMINAL and TPNOMINAL are recorded/computed as described above. Then the participant changes cognitive sets by speeding up or slowing down, or proceeding with more or less attention to accuracy. If the user slows down, taking about 10% longer for each selection, we expect a slight improvement in accuracy, i.e., a lower SDx. How much change in SDx will actually take place and what is the corresponding throughput? This is the central question addressed in this research.
Under the hypothesis of "no change in throughput across cognitive sets", we compute the expected accuracy, by rearranging the equation with SDx on the left and using 1.10 × MTNOMINAL and TPNOMINAL on the right. In other words, we keep TP constant, increase MT by 10% (MT factor = 1.10) and calculate what SDx must be so that user behaviour under the new cognitive set yields the same throughput as in the nominal condition. This can been done for a range of cognitive sets, increasing/decreasing MT by 10%, 20%, and so on, and computing the required SDx for constant throughput. This exercise is shown in Figure 1 with the curved line showing SDx-MT conditions producing constant throughput.
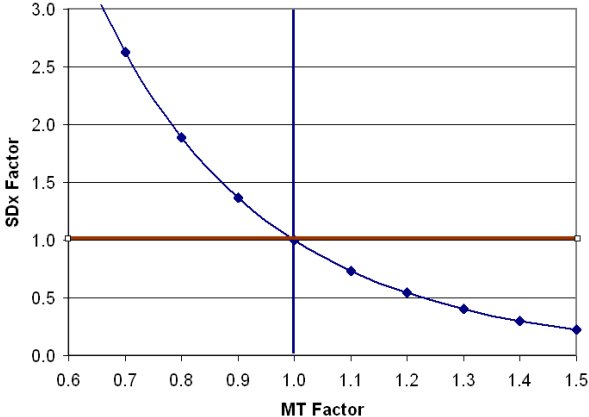
Figure 1. Changes in speed (MT Factor) and accuracy (SDx Factor) yielding constant throughput
While the exercise above is interesting, it remains to be seen whether the conjectured behaviour occurs in practice. If a participant changes their emphasis toward speed or accuracy, is the throughput computed under each condition the same, or is it different?
METHOD
Our experiment is deliberately simple as it uses a reverse-burden methodology, because we cannot "prove a negative". If we "fail to reject" (.05 < p < 1) the conventional null hypothesis – no change in the dependent variable (throughput) across levels of the independent variable (cognitive set) – this is evidence supporting, but not proving, the constant-throughput hypothesis.
Participants
We recruited 18 volunteers (5 female, 13 male) from the local university. The mean age was 27.8 years (SD = 4.88). All participants were experienced mouse users, reporting 3-12 hours of daily computer usage.
Apparatus
The experiment was conducted using a conventional workstation (see Figure 2). The participants were allowed to adjust the height and location of the chair and relocate the mouse to achieve a comfortable working posture.

Figure 2. Workstation used in the experiment
The mouse was an optical USB Microsoft IntelliMouse with four buttons and a scroll wheel. The experimental software, written in Java, presented the task and saved the mouse coordinates, timestamps, and other summary information at the end of each trial block.
Task
The task is shown in Figure 3. We used a traditional Fitts' law reciprocal tapping task with a nominal Index of Difficulty of 4.24 bits. The width (W) of the bars was 25 pixels and the distance (A) between the center points of the bars was 400 pixels. A red cross indicated the bar to select. With each mouse click, the cross moved to the opposite bar. The trials were organized in blocks of 20. A popup window appeared after each block displaying the mean movement time, number of errors, and We.

Figure 3. Task presented to participants
Errors were allowed. Clicks outside the target were accompanied with a beep. Participants were instructed to continue the task in the event of an error. However, blocks with more than eight errors were repeated until the error count was eight or less.
The standard arrow-shaped Windows cursor was used with the hot-spot at the tip of the arrow, as usual. According to Windows convention, selection occurred when the mouse button was lifted.
Procedure
Participants were first explained the overall procedure. This was followed with practice trials. The participants were instructed to relax and work comfortably while performing the task as fast and accurately as possible. While they were told that a perfect click is exactly in the middle of the target bar and they should aim for this, they were also told that it is OK to hit anywhere on the target.
The basic unit in the procedure was a "set", defined as five blocks of 20 clicks each. Sets were used for both warm-up and data collection. There were four data-collection sets: a pre-test nominal set first, followed by either a nominal set, a speed-emphasis set, or an accuracy-emphasis set. The latter three sets were counterbalanced using 3! = 6 different orders. With 18 participants, each order was used by three participants.
After the pre-test nominal condition, the mean movement time was immediately computed (using a custom utility program) and written on a piece of paper along with values 10% shorter and 10% longer. The paper was placed in front of the participant. These values were used in the warm-up sets to rehearse the desired timing.
Each data-collection set was preceded by a warm-up set. For warm-up, participants could terminate early if it was felt (and confirmed by the investigator) that the trials were proceeding correctly according to the condition. However, at least two blocks were completed in each warm-up set.
In the accuracy-emphasis condition, we instructed participants to proceed more accurately. We told them that it is OK if movement time increases. The increase was to happen because of increased accuracy, not because of lazy performance. The participant was instructed to work accurately enough to make the mean movement time at least 10% longer than in the initial nominal condition.
Under speed-emphasis, we instructed participants to perform faster. We told them that this would probably mean that they would not perform as accurately as in the nominal condition. The movement time was required to decrease by at least 10% from the initial nominal condition.
Maintaining the desired movement time with each condition was achieved by comparing the time on the sheet to the mean movement time in the popup window at the end of each block, and adjusting in the next block, if necessary. If the participant was pointing too fast, he or she was instructed to be more accurate in the next block. If the movement time was too long, he or she was instructed to perform faster. Because the participants were aiming for the same movement time, it was impossible for learning to affect the movement time. If learning occurred, it should show as increased accuracy.
Data considerations and treatment of outliers
The effective target width computation (We = 4.133 × SDx) is sensitive to certain kinds of outliers. For example, an accidental double-click on a target inflates We beyond reason. This occurs because the second click is interpreted as a trial with little of no movement amplitude.
Our criterion for determining outliers was as follows. A trial was removed if (a) the selection coordinates were outside the current target and (b) the distance moved after the previous click was less than A / 2 or the distance to the center of the current target was larger than 2W. If a block contained an outlier, as above, it was repeated.
Design
In summary, the experiment was a 3 × 5 repeated measured design with the following factors and levels:
Cognitive set nominal, speed-emphasis, accuracy emphasis Block 1, 2, 3, 4, 5
There were three dependent variables: speed (movement time in seconds), accuracy (% errors), and throughput (bits/s). The primary goal of the experiment was to investigate the effect of cognitive set on throughput, and, to a lesser extent, on speed and accuracy.
Excluding warm-up trials and the pre-test nominal condition, the experiment involved 18 participants × 3 cognitive sets × 5 blocks × 20 trials per block = 5,400 trials.
RESULTS AND DISCUSSION
Outliers
Of the 270 blocks in the experiment, eight where repeated because one or more trials was deemed an outlier according to the criteria describe above.
Speed and Accuracy
As expected, there was a highly significant effect of cognitive set on movement time (F2,34 = 372.7, p < .0001). The mean of 756 ms for the nominal condition dropped by 19.0% to 613 ms for the speed-emphasis conditions and increased by 26.3% to 947 ms for the accuracy-emphasis condition. This is shown in Figure 4.
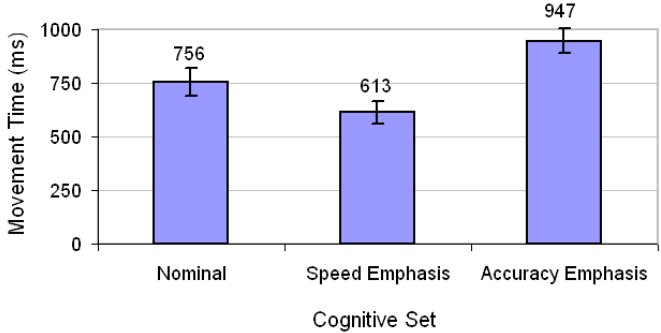
Figure 4. Movement time (ms) by cognitive set. Error bars show ±1 standard deviation.
There was also a significant effect of cognitive set on accuracy (F2,34 = 91.83, p < .0001). As seen in Figure 5, the 2.56% error rate for the nominal condition increased substantially to 19.01% for the speed-emphasis condition while dropping to a very low 0.28% for the accuracy-emphasis condition.
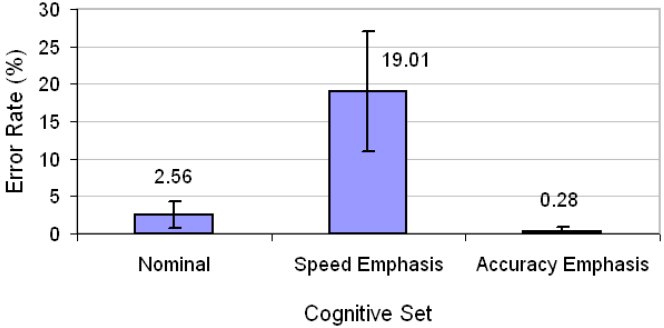
Figure 5. Accuracy (Error Rate in %) by cognitive set
The results for speed and accuracy are fully expected. The results above simply confirm, for example, that when participants were asked to increase their speed, they did, and the result was a decrease in accuracy.
Throughput
Our main motivation was to investigate whether changes in the cognitive set for speed and accuracy would influence the dependent variable throughput. Figure 6 shows the effect of cognitive set on throughput.
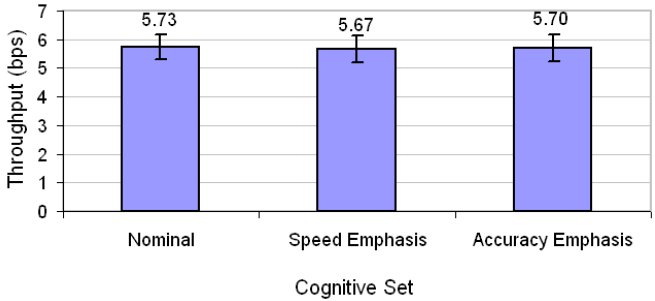
Figure 6. Throughput (bits/s) by cognitive set
The offsetting effect of speed and accuracy in the computation of throughput is clearly seen. The values in Figure 6, about 5.7 bit/s, are all within 1% of each other. Cognitive set clearly has little or no effect on throughput, unlike the effect on speed or accuracy alone. The essentially flat outcome in Figure 6 is accompanied by a non-significant F-test in an analysis of variance (F2,34 = 0.149, ns). In a statistical sense, this means we fail to reject the null hypothesis. The null hypothesis – no significant effect of cognitive set on throughput – holds.
Demonstration of Constant Throughput
To further explain the results, we re-visit our earlier example using data from the experiment. A chart similar to Figure 1 was constructed for each participant. The chart for P18 is shown in Figure 7 as an example. The central point is the mean of the MT and SDx values in the five blocks of trials for the nominal condition. From these values, the curve for constant throughput is established. Each marker shows the result for a block, with large makers showing the aggregate result for the speed-emphasis (triangle), nominal (circle) and accuracy-emphasis (square) conditions.

Figure 7. Changes in speed (MT Factor) and accuracy (SDx Factor) with constant throughput – Participant #18
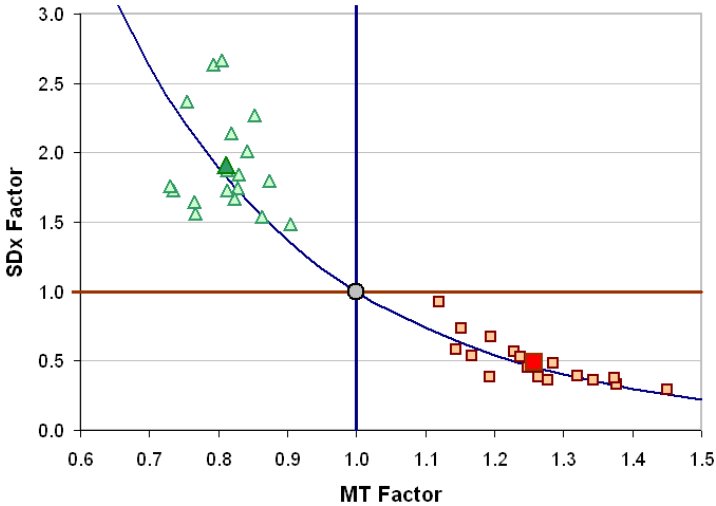
Figure 8. Changes in speed (MT Factor) and accuracy (SDx Factor) with constant throughput – all participants
Figure 8 is the same except each point is the aggregate response for one participant. The absence of points between 0.9 × MT and 1.1 × MT is evidence that the procedure worked. The increase in the variability in SDx at the speed-emphasis (left) side of Figure 8 is an interesting phenomenon, but is not unexpected, as it is well known that behaviour is more erratic when humans act with haste [2].
CONCLUSIONS AND FUTURE WORK
This work provides empirical evidence in support of an important but difficult-to-test tenet of Fitts' law: that throughput is independent of the speed-accuracy tradeoff. Subsequent research could explore, for example, whether a log or other relationship can capture and normalize the changing spread in points moving right to left in Figure 8.
ACKNOWLEDGMENT
This research is sponsored by the Natural Sciences and Engineering Research Council of Canada and the Academy of Finland (project 53796).
REFERENCES
1. Fitts, P. M. and Radford, B. K., Information capacity of discrete motor responses under different cognitive sets, J Exp Psych, 71, 1966, 475-482.
2. Kantowitz, B. H. and Sorkin, R. D., Human factors: Understanding people-system relationships. New York: Wiley, 1983.
3. MacKenzie, I. S., Fitts' law as a research and design tool in human-computer interaction, Human-Computer Interaction, 7, 1992, 91-139.
4. Soukoreff, R. W. and MacKenzie, I. S., Towards a standard for pointing device evaluation: Perspectives on 27 years of Fitts' law research in HCI, Int J Human-Computer Studies, 61, 2004, 751-789.
5. Zhai, S., Characterizing computer input with Fitts' law parameters: The information and non-information aspects of pointing, Int J Human-Computer Studies, 61, 2004, 791-801.