---

Castellucci, S. J., and MacKenzie, I. S. (2009). TnToolkit: A design and analysis tool for ambiguous, QWERTY, and on-screen keypads. Proceedings of the ACM Symposium on Engineering Interactive Computing Systems – EICS 2009, pp. 55-60 New York: ACM. [PDF]

---

TnToolkit: A Design and Analysis Tool for Ambiguous, QWERTY, and On-Screen Keypads

Steven J. Castellucci and I. Scott MacKenzie

Department of Computer Science and Engineering
York University Toronto, Ontario M3J 1P3 Canada
{stevenc, mack}@cse.yorku.ca

ABSTRACT
The pervasive use of ambiguous keypads for mobile text entry necessitates examination of their performance characteristics. This paper presents TnToolkit – a self-contained tool to calculate performance measurements for ambiguous keypads. While TnToolkit's focus is ambiguous keypads, it also works with QWERTY and on-screen keypads. By default, TnToolkit predicts words-per-minute performance based on a traditional Fitts' law model, and calculates KSPC, the average keystrokes required to enter each character of text. Existing modules are extensible to implement custom metrics. An experiment reveals that using TnToolkit to gather performance metrics is 69% faster than existing techniques, without compromising accuracy.

Categories and Subject Descriptors
H.5.2 [Information interfaces and presentation]: User Interfaces – Evaluation/methodology.

General Terms: Measurement, Performance, Design, Human Factors

Keywords: Toolkit, text entry, performance measurement, ambiguous keypads, keystrokes-per-character, words-per-minute

1. INTRODUCTION

Unlike a QWERTY keyboard, an ambiguous keypad assigns multiple letters to each key. Consequently, ambiguous keypads use fewer than 26 keys for English text entry. Moreover, the keypads are smaller and reduce finger movement. However, assigning multiple letters to a key creates ambiguity, since a sequence of keystrokes can map to more than one word. In this case, additional keystrokes are needed to select the intended word. A favourable text entry technique reduces the number of keys, while imposing minimal overhead. The toolkit presented here provides a fast and accurate analysis of ambiguous keypad characteristics, including text entry performance in words per minute (WPM) and keystrokes-per-character (KSPC).

The ubiquitous telephone keypad is an example of an ambiguous keypad. Even the popular Nintendo Wii video game console provides an on-screen telephone keypad in its Message Board application (Figure 1). Familiarity with the telephone keypad for text entry is due to the pervasive use of mobile phones for sending Short Message Service (SMS) messages (a.k.a. text messages). In 2008, Americans sent more than 3.5 billion text messages per day [10]! Such immense use of ambiguous keypads underscores the importance of tools to analyse and evaluate new and exiting designs.

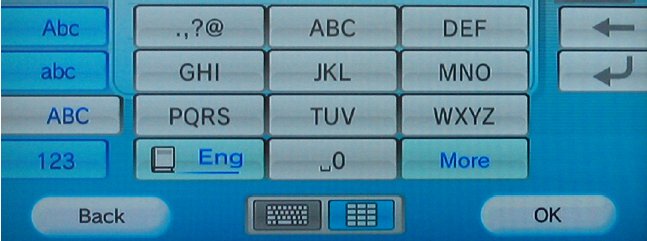
Figure 1. The ambiguous keypad used in the Nintendo Wii's Message Board application.

After reviewing text entry concepts, we present our motivation for TnToolkit, describe its features, and compare it to related work. We then detail a user study comparing TnToolkit to an existing analysis method.

1.1 Language-Based Disambiguation

With ambiguous text entry, each key press maps to a small set of letters. Consequently, a sequence of keystrokes can map to more than one word. For example, on a standard telephone keypad, 2-2-5-3 could represent "cake", "able", "bald", or "calf". This outcome is called a collision and requires additional input to select the intended word.

Tegic Communications (http://www.tegic.com) developed the T9 text entry technique that combines a telephone keypad with language-based modelling. Words involved in a collision appear in decreasing order of frequency. The user traverses the sequence by pressing a next key. Using the previous example, entering "able" would involve one key press for each letter, one press of next to select "able" from the list, and one press of SPACE to select and terminate the word.

1.2 Keystrokes-per-Character (KSPC)

The keystroke overhead with ambiguous keypads depends on the text entry technique. A metric that captures this overhead is keystrokes-per-character (KSPC) [6]. KSPC is the average number of keystrokes required to enter a single character of text in a given language using a given interaction technique. (For on-screen keypads, "keystrokes" could represent stylus or finger taps [6].) KSPC26 accounts for letters, while KSPC27 includes the space character. KSPC is calculated as follows:

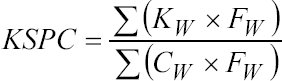
For each word in the corpus, the number of characters (C_W, including a terminating space) and the required number of keystrokes (K_W) are both weighted by the word's frequency in the corpus (F_W). A KSPC of 1 is characteristic of QWERTY keyboards. While a low KSPC is desirable, a value less than 1 is only possible using word completion or word prediction techniques.

1.3 WPM Performance Prediction

Fitts' law [2] predicts the movement time (MT) to a target of width W at a distance (a.k.a. amplitude) A. Provided the units for both measures are the same, the division of A by W "cancels out" the units. Thus, only the distance-to-width ratio is needed. A movement time prediction uses W and A, and empirically defined coefficients a and b:

An upper-bound WPM prediction can be calculated using Fitts' law, a language corpus in the form of a word-frequency list, the relative location and size of each key, and the letters assigned to each key [12]. For simplicity, we assume English is the intended language and movement time is in seconds. The first step is to generate a prediction of the movement time from one key press to the next using Fitts' law. By summing the movement times to enter each character of each word, one can calculate the predicted time to enter each word in the corpus and, hence, the time to enter the entire corpus (weighted by word frequency).

Modelling one-handed text entry depends solely on calculating MT. However, two-handed typing involves two digits (i.e., fingers or thumbs) working in parallel. In this case, predicting movement time involves considering both the time to move the same digit from one key the next key and the time to move the alternate digit from its previous position. The reader is directed to previous research on two- thumb text entry for further details [9].

Dividing the total entry time by the number of characters (including spaces) in the corpus yields the average time to enter a character (in seconds per character). Taking the reciprocal and multiplying by 60 / 5 yields a prediction of the average text entry speed in words per minute.¹ This technique can apply equally to ambiguous, QWERTY, and on-screen keypads.

2. MOTIVATION

Our work builds upon previous research [6, 9] that used command-line tools to calculate KSPC and WPM.

The basic ingredient to obtain KSPC for a keypad layout is a corpus in the form of a word-frequency list. Each line contains a word and its frequency within the corpus. The keystrokes to enter each word are constructed based on the interaction technique of interest and appended to each entry in the file. Collision-resolving keystrokes are also included where necessary. The resulting word-frequency-keystroke file is used as input to the model which calculates KSPC by weighting the keystroke count for each word by its frequency.

Calculating text entry speed (WPM) is a multi-step process. It involves the word-frequency-keystroke file previously detailed, Fitts' law coefficients, and a keypad digitization file. Each line in the digitization file encodes a different key on the keyboard using a unique identifier (e.g., a letter), the x- and y-coordinate of the key's location, and the target width of the key [9].

Gathering data for the digitization file requires an image of the keypad. If using existing command-line tools, a graphics application is also required. The image must be to-scale and the application must display the coordinates of the mouse pointer. The user opens the image within the graphics application and uses the mouse pointer as a probe to determine the coordinates of a key. The key width is similarly determined. However, the use of a separate graphics application is cumbersome.

We created a self-contained tool called TnToolkit to facilitate the rapid evaluation and analysis of ambiguous keypads. TnToolkit calculates KSPC characteristics and predicts WPM performance modelling one- or two-handed text entry. Though our research focuses on physical ambiguous keypads, TnToolkit also works with soft keypads (i.e., on-screen or touch-screen keypads) and QWERTY keypads. Furthermore, it is extensible to serve as the framework for implementing new characteristics-based or performance-based metrics.

While Tegic Communications' T9 technology stands for "Text on 9 keys" [13], our toolkit evaluates similar techniques that use an arbitrary n number of keys – hence the name TnToolkit.

3. FEATURES AND BENEFITS

TnToolkit's distributable package can be downloaded from http://www.cse.yorku.ca/~stevenc/TnToolkit/. Upon starting the toolkit's GUI interface (Figure 2), the user loads an image of the keypad. The user digitizes a key by dragging across its region within the image.

Upon releasing the mouse button, the Key Definition dialog (Figure 3) facilitates letter-key mapping. The user indicates whether the key encodes letters, SPACE, or next. For letter keys, the user selects one or more letters to associate with the key. (For QWERTY layouts, only one letter is selected per key.) Letters already mapped to keys are disabled.

Finally, the user stipulates whether one typically presses that key with the left thumb, right thumb, or either thumb. (The term "thumb" also includes using a finger on each hand or using two styli simultaneously.) Assigning all keys to a single thumb simulates one-handed input.

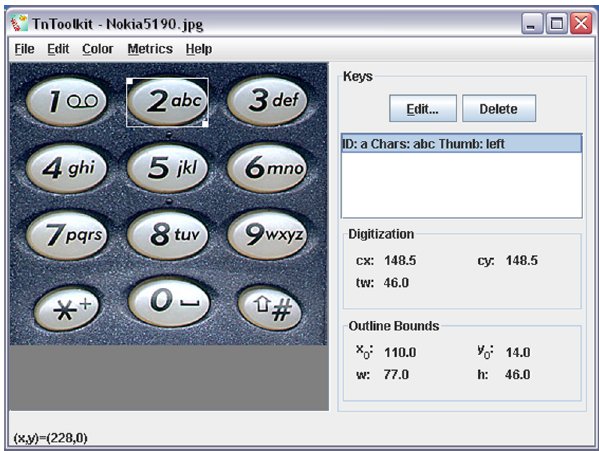
Figure 2. TnToolkit's main screen. A key has been digitized and selected.

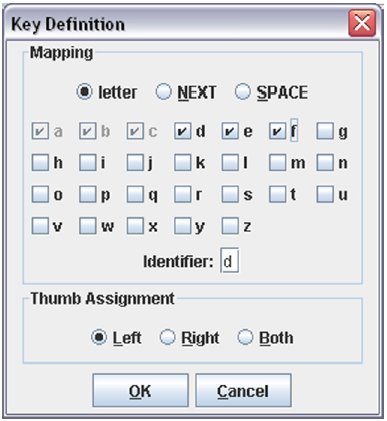
Figure 3. The dialog used to map letters to keys.

Digitized keys appear as entries in the list on the right of the main window. The user can delete the digitization or edit the letter-key mapping. The attributes of the selected key also appear. The values x₀ and y₀ represent the top left point of the key's outline, and the values w and h represent its width and height, respectively. The key's target width (t_w) is the smaller of its width and height [7], and the key's target point is its centre point, represented by c_x and c_y. This form of digitization is consistent with previous tools [9, 12].

Clicking within a key's outline selects it. The user can then drag the top-left handle to move the outline, or drag the bottom-right handle to resize the outline. The user can change the colour of outlines to make them clearly visible. In addition, the user can undo or redo actions without limitation – a feature not always available in graphics applications.

When the user has mapped all letters and functions to keys, the KSPC and WPM metrics can be calculated. A Parameters Dialog is available to specify Fitts' law coefficients and a word-frequency file. Calculated metrics, ambiguous word sets (i.e., words associated with collisions), and word-frequency-keystroke data, appear in a tabbed dialog (Figure 4 and Figure 5). The contents of these panes can be copied to the clipboard for use in other programs.

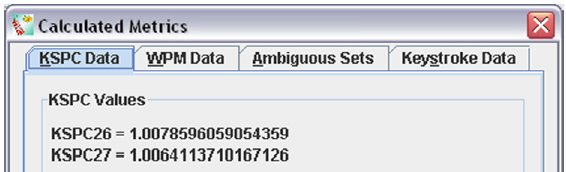
Figure 4. The KSPC data calculated for T9 input.

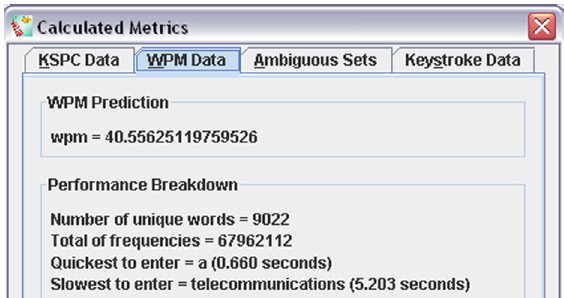
Figure 5. The WPM data calculated for T9 input.

4. RELATED WORK

Composed of goals, operators, methods, and selection rules, the GOMS model [1] proposed by Card, Moran, and Newell is the standard for predicting human performance in interaction systems. However, in practice, the overhead required to produce GOMS models often eclipses their benefit [14]. Tollinger et al. use GOMS modelling in X-PRT, an environment to support interface design and performance evaluation [14]. In general, X-PRT simplifies modelling by allowing users to import screen images and outline interactive widgets. While X-PRT is applicable to a broad spectrum of interaction, TnToolkit specializes in text entry. Consequently, it is more straightforward and suitable for such tasks.

A subset of GOMS is the Keystroke-Level-Model (KLM) [1]. Using KLM, completion time is predicted by decomposing a task into primitive operations. KLM operators are combined according to a set of rules. Syntagm provides a "KLM Calculator" [4] to aid this process. Luo and John validated KLM on mobile devices [5] and Holleis et al. introduced mobile interaction operators [3]. While these contributions can model various mobile interactions, TnToolkit is specifically designed for text entry analysis.

An evaluation tool by Sandnes models text entry techniques using finite state automata [11]. Traversal algorithms can then evaluate the resulting directed graphs and calculate KSPC. However, the lack of spatial details precludes prediction of WPM performance.

As an alternative to software-based tools, MacKenzie and Read employed paper mock-ups of keypad layouts to evaluate text entry performance [8]. Using their simple, low-tech approach, numerous user study sessions can be held simultaneously. Furthermore, their results were consistent with formal studies. However, lack of a computer results in imprecise timing and accuracy measurements. Combined with TnToolkit, this approach could quickly yield Fitts' coefficients for the performance model and reveal both novice and expert performance.

In the following section, we detail our methodology to evaluate the performance and accuracy of TnToolkit.

5. METHOD

5.1 Participants

Twelve volunteer participants (ten male, two female) were recruited from the local university campus. All understood English proficiently. Ages ranged from 22 to 38 years (mean = 27 years). Though all participants chose to use the mouse in their right hand, two participants were actually left-handed. Testing time for each participant was approximately thirty minutes. None had any previous experience with TnToolkit.

5.2 Apparatus

The workstation was a Pentium 4 530 (3 GHz) system running Windows XP. It was equipped with a 17-inch LCD monitor and a Logitech Internet Keyboard and Optical Mouse. The experiment took place in a quiet office environment.

5.3 Procedure

Participants were given the task of calculating KSPC and WPM for the keypad shown in Figure 2. To allow for comparisons with established results, this study employed the same model parameters used in previous research [12]. These parameters include the keypad layout, a word-frequency file, the Fitts' law coefficients, and one-hand interaction.

Each participant performed the task once with command-line tools and once with TnToolkit. In each case, participants were given a written script to guide them through each condition. Timing started when the participant indicated that s/he was ready to begin and stopped when the participant finished recording KSPC and WPM.

5.3.1 Command-Line

In this condition, participants used existing command-line programs [6, 9] to calculate KSPC and WPM.

The first step was to use Microsoft Notepad to create a keypad digitization file. The script instructed participants to define the letter keys (keys 2-9), next (*), and SPACE (0). Participants used Microsoft Paint (and Calculator if necessary) to determine coordinate values. A key's target point was its centre, and its target width was the smaller of its width and height [7].

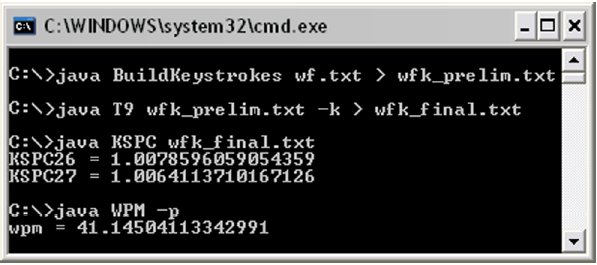
Figure 6. A demonstration of the command-line programs.

Participants executed three programs at the command-line (Figure 6). The first program read the word-frequency file and produced a word-frequency-keystrokes file. This was accomplished by replacing each letter in a word by the corresponding number on the telephone keypad. The second program appended disambiguating keystrokes (representing presses of next) in accordance with T9-like input. The third program yielded KSPC26 and KSPC27.

Calculating a WPM performance prediction required the participants to enter the following data into a model definition file: the keypad digitization filename, the word-frequency-keystrokes filename, and the text entry keys' identifiers. This model definition file served as input to a program that yielded a WPM performance prediction.

5.3.2 TnToolkit

In this condition, participants launched TnToolkit and opened the image of the keypad. The script instructed them to define the letter keys (keys 2-9), next (*), and SPACE (0). The script also indicated how to edit a key's parameters. After defining the required keys, the participants selected Calculate from the Metrics menu to display the KSPC measurements and WPM performance prediction.

5.4 Design

This experiment was a single factor design. The within-subjects factor was interface type with two levels: command-line versus TnToolkit (GUI). The order of factors was counterbalanced to offset learning effects. The two dependent variables were task completion time and result accuracy (percent difference). Accuracy was measured as the deviation between the two interface types in their results for KSPC and WPM.

6. RESULTS AND DISCUSSION

All participants appreciated the convenience of TnToolkit. Some believed its use would reduce the occurrence of errors and make errors easier to identify and correct.

6.1 Task Completion Time

Participant performance, as measured by task completion time, appears in Table 1.

Table 1. The results for task completion time.
(Green indicates the faster condition.)

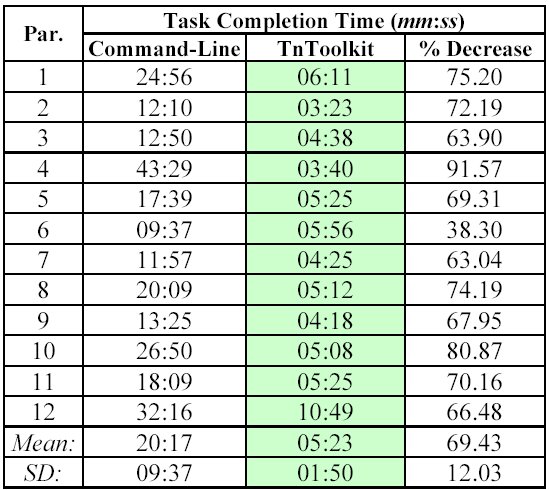
An analysis of variances revealed that interface type had a significant effect on task completion time (F_1,10 = 25.88, p < .0005). On average, task completion time was 69% less using the integrated TnToolkit than using auxiliary applications with the command-line programs. In addition, an ANOVA confirmed that counterbalancing was effective with non-significant effects for group (F_1,10 = 0.044, ns) and group by interface type (F_1,10 = 0.013, ns).

Because digitizing a keypad involves a graphical component, it might seem obvious that incorporating a GUI around existing command-line tools would improve user performance. However, this evaluation yields a quantitative, statistically significant, and large improvement effect.

The lower standard deviation in the TnToolkit condition reveals that participant performance was more consistent with the toolkit than with the command-line tools. Considering that participants had no previous experience with the toolkit, this suggests users can quickly become proficient with it. However, regardless of experience, using the command-line tools requires manual calculation of a key's centre coordinates and generation of various input files. In contrast, TnToolkit performs such operations automatically. We therefore hypothesize that experience would decrease task completion time in both conditions, but that TnToolkit would remain faster.

6.2 Result Accuracy

Because both the letter-key mapping and the word-frequency file remained the same throughout the experiment, all participants obtained the same KSPC measurements in both conditions. Unpublished statistics verify the KSPC26 value of 1.0079 and the KSPC27 value of 1.0064. (Published results [6] differ by less than 0.08%, but were calculated using a slightly different word-frequency file.)

Table 2. The WPM predictions and accuracy with respect
to the established prediction of 40.6 wpm [12].
(Green indicates the more accurate condition.)

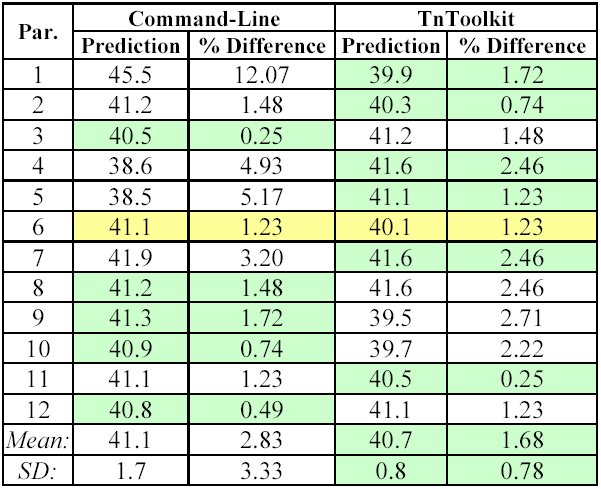
Table 2 presents the WPM predictions calculated by each participant in each condition. It also presents the percent difference from the established prediction of 40.6 wpm for this keypad [12]. Again, statistical analysis confirms effective counterbalancing (F_1,10 = 1.32, p = .280) and that no asymmetric transfer of skill occurred between the two conditions (F_1,10 = 3.19, p = .105).

Using the toolkit, all participants attained a prediction within 3% of the accepted value. Seven of twelve participants achieved the same or better accuracy with the TnToolkit than with the command-line programs. However, this difference was not statistically significant (F_1,10 = 1.73, p = .216). While this indicates that the toolkit does not necessarily reveal more accurate results, it also suggests that using the TnToolkit is just as accurate as the much slower alternative.

7. CONCLUSION AND FUTURE WORK

With the global proliferation of mobile devices and popularity of text messaging, readily obtainable performance measurements are important for the a priori evaluation of design alternatives. TnToolkit rapidly and accurately analyzes the performance characteristics of keypads. It streamlines performing letter-key assignments and simplifies digitizing ambiguous keypads. Furthermore, it allows users to visualize and easily edit the keypad digitization and share data with other applications.

The evaluation revealed the benefits of TnToolkit. Its use resulted in a 69% decrease in task completion time without compromising accuracy. As we continue our research on text entry metrics, TnToolkit will be expanded to facilitate additional performance evaluations. Furthermore, a longitudinal study may reveal additional toolkit benefits or areas for improvement. By conveniently facilitating the performance evaluation of ambiguous keypad designs, TnToolkit facilitates analyses of existing devices as well as new prototypes.

8. ACKNOWLEDGMENTS

We wish to thank the EICS reviewers for their constructive feedback. This research was funded by the Natural Sciences and Engineering Research Council of Canada.

9. REFERENCES

[1]	Card, S. K., Moran, T. P., and Newell, A., The Psychology of Human-Computer Interaction. Hillsdale, NJ: Erlbaum, 1983.
[2]	Fitts, P. M., The information capacity of the human motor system in controlling the amplitude of movement, Journal of Experimental Psychology, 47, 1954, 381-391.
[3]	Holleis, P., Otto, F., Hussmann, H., and Schmidt, A., Keystroke-level model for advanced mobile phone interaction, Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, New York: ACM (2007), 1505-1514.
[4]	Hudson, W., Keystroke Level Model Calculator. (Accessed on April 10, 2009.) http://www.syntagm.co.uk/design/klmcalc.shtml.
[5]	Luo, L. and John, B. E., Predicting task execution time on handheld devices using the keystroke-level model. Proceedings of Extended Abstracts on Human Factors in Computing Systems, New York: ACM (2005), 1605-1608.
[6]	MacKenzie, I. S., KSPC (keystrokes per character) as a characteristic of text entry techniques, Proceedings of the 4th International Symposium on Mobile Human-Computer Interaction, Berlin: Springer-Verlag (2002), 195-210.
[7]	MacKenzie, I. S. and Buxton, W., Extending Fitts' law to two-dimensional tasks, Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, New York: ACM (1992), 219-226.
[8]	MacKenzie, I. S. and Read, J. C., Using paper mockups for evaluating soft keyboard layouts, Proceedings of CASCON 2007. Toronto: IBM Canada Ltd., (2007), 98-108.
[9]	MacKenzie, I. S. and Soukoreff, R. W., A model of two-thumb text entry, Proceedings of Graphics Interface 2002, Toronto: Canadian Information Processing Society (2002), 117-124.
[10]	Roche, R., CTIA Semi-Annual Wireless Industry Survey, CTIA The Wireless Association. (Accessed on April 1, 2009.) www.ctia.org/media/press/body.cfm/prid/1811.
[11]	Sandnes, F. E., Evaluating mobile text entry strategies with finite state automata, Proceedings of the 7th International Conference on Human-Computer Interaction with Mobile Devices & Services, New York: ACM (2005), 115-121.
[12]	Silfverberg, M., MacKenzie, I. S., and Korhonen, P., Predicting text entry speed on mobile phones, Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, New York: ACM (2000), 9-16.
[13]	T9, T9 Text Input Home Page. (Accessed on April 10, 2009.) http://www.t9.com/us/learn/.
[14]	Tollinger, I., Lewis, R. L., McCurdy, M., Tollinger, P., Vera, A., Howes, A., and Pelton, L., Supporting efficient development of cognitive models at multiple skill levels: Exploring recent advances in constraint-based modeling, Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, New York: ACM (2005), 411-420.
[15]	Yamada, H., A historical study of typewriters and typing methods: from the position of planning Japanese parallels, Journal of Information Processing, 2, 1980, 175-202.

Footnotes

1. For approximately the past 100 years, calculating text entry speed assumes a word length of five characters (including spaces) [15].