MacKenzie, I. S., and Soukoreff, R. W. (2002). A character-level error analysis technique for evaluating text entry methods. Proceedings of the Second Nordic Conference on Human-Computer Interaction -- NordiCHI 2002, pp. 241-244. New York: ACM. [software]
A Character-level Error Analysis Technique for Evaluating Text Entry Methods
I. Scott MacKenzieDept. of Computer Science
York University
Toronto, Ontario Canada M3J 1P3
smackenzie@acm.org
R. William Soukoreff
Dept. of Computer Science
York University
Toronto, Ontario Canada M3J 1P3
will@acm.org
ABSTRACT
We describe a technique to analyse character-level errors in evaluations of text entry methods. Using an algorithm for sequence comparisons, we generate the set of optimal alignments between the presented and transcribed text. Per-character errors, categorized as insertions, substitutions, or deletions, are obtained by analysing the alignments and applying a weighting factor. A detailed example using a real data set is given.KEYWORDS
Text entry, error rates, mobile computing, minimum string distance, sequence comparison, optimal alignments
INTRODUCTION
Recently [2], we presented a technique for measuring the percentage of errors in evaluations of text entry methods. This paper begins by briefly reviewing the rationale, strengths, and weaknesses of the technique. Following this, we describe an extension of this work to further analyse errors in ways not previously possible. Instead of measuring only the overall error rate (as before), the new technique enumerates errors on a per-character basis, for example, the occurrences of the letter "b" incorrectly entered. These analyses are important since they can determine effects such as which key assignments are error prone for keyed entry, or which handwritten strokes are frequently misrecognized for stylus entry. We then extend the technique further by creating a "confusion matrix" − a table or chart showing what errors occurred, for example, the incidences of the letter "b" entered as "p".
EVALUATIONS OF TEXT ENTRY METHODS
The drive toward mobility in computing, and, in particular, the popularity of SMS messaging, has fuelled a resurgence in research in one of the oldest areas in office automation: text entry. Potential text entry methods or devices are developed and then evaluated in controlled experiments that pit one technique against another. The evaluations typically require participants to enter phrases of text using each technique while performance measures are gathered for follow-up analyses.The performance measures of greatest interest are speed and accuracy. Speed, in words per minute, is relatively easy to measure, however, the same is not true of accuracy. The intuitively simple measure "error rate" is deceptively difficult to measure. For example, consider the following presented (top) and transcribed (bottom) text:
quickly
qucehkly
What is the error rate? A simple character-wise comparison suggests that all letters after the "u" are incorrect. However, the
final three ("kly") appear correct, despite misalignment. The difficulty in automating the tabulation of such errors has been
the bane of text entry research for many years. Two possible solutions are to preclude errors (the user must correctly enter
each character before proceeding), or to impose a procedure wherein users maintain alignment with the presented text
(following every error, the user must resynchronise with the presented text). In the latter case, errors are tallied by a simple
character-wise comparison of the presented and transcribed texts. However, both procedures are unnatural and this
compromises the external validity of the experiment.The following section briefly describes the technique presented earlier [2] to measure error rates. The main advantage is that the technique works even in situations where the user occasionally inserts or deletes characters, as naturally occurs in typical usage. Thus, a constrained and unnatural experimental procedure is avoided.
MINIMUM STRING DISTANCE
The first step is to calculate the minimum string distance (MSD) between the presented and transcribed text strings. This is the minimum number of primitive operations − substitutions, insertions, or deletions − to transform one string into the other. The MSD statistic is viewed as the number of errors committed by the user while entering the presented text string. Given this, we proposed the following as an error rate measure for text entry tasks:
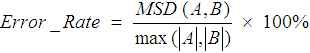
| (1) |
where A and B are the presented and transcribed text strings. Using the maximum length of the two strings in the denominator simply ensures an upper limit of 100% for the error rate. We will say more about Equation 1 shortly.
Let us further consider the strings above. The MSD algorithm [2] generates the following matrix
q u c e h k l y
0 1 2 3 4 5 6 7 8
q 1 0 1 2 3 4 5 6 7
u 2 1 0 1 2 3 4 5 6
i 3 2 1 1 2 3 4 5 6
c 4 3 2 1 2 3 4 5 6
k 5 4 3 2 2 3 3 4 5
l 6 5 4 3 3 3 4 3 4
y 7 6 5 4 4 4 4 4 3 <-- MSD
with the MSD statistic in the bottom-right cell. Thus,
|
| (2) |
OPTIMAL ALIGNMENTS
In this section we extend our earlier work by presenting a technique to enumerate the errors on a per-character basis. In the example just presented, MSD = 3; however, this says little about the actual errors committed. Yes, three errors were committed, but what were the errors?In fact, there are often multiple answers to this question, because more than one minimum set of transformations may exist for the computed MSD. Each transformation is called an "alignment", and represents a possible explanation of the errors made. For the example, there are four such "optimal alignments":
quic--kly
qu-cehkly
quic-kly
qucehkly
qui-ckly
qucehkly
qu-ickly
qucehkly
In the illustrations, a dash in the top string represents an insertion, while a dash in the bottom string represents a deletion.
Where letters differ in the top and bottom, a substitution occurred. A quick visual scan of the alignments reveals three
primitive errors in each. This is expected since MSD = 3. Note also that the top alignment has nine characters, whereas the
remaining three have eight.For completeness, we include the pseudo code for an algorithm to generate the set of optimal alignments. Align receives as arguments the two strings (character arrays A & B), the MSD matrix (D), two integers (X & Y), and two alignment strings (AA & AB). X and Y are initialised with the coordinates of the bottom-right cell in the matrix, while AA and AB are initially null.
Align(A, B, D, X, Y, AA, AB)
if (X == 0 && Y == 0)
output AA, AB
return
if (X > 0 && Y > 0)
if (D[X][Y] == D[X-1][Y-1] && A[X-1] == B[Y-1])
Align(A, B, D, X-1, Y-1, A[X-1]+AA, B[Y-1]+AB)
if (D[X][Y] == D[X-1][Y-1] + 1)
Align(A, B, D, X-1, Y-1, A[X-1]+AA, B[Y-1]+AB)
if (X > 0 && D[X][Y] == D[X-1][Y] + 1)
Align(A, B, D, X-1, Y, A[X-1] + AA, "-" + AB)
if (Y > 0 && D[X][Y] == D[X][Y-1] + 1)
Align(A, B, D, X, Y-1, "-" + AA, B[Y-1] + AB)
return
The algorithm recurses through the
D matrix from bottom-right to top-left, constructing the alignment strings in
AA and
AB.
All optimal paths through the matrix are traversed. Alignments are outputted upon reaching the top-left of
D.
CHARACTER-LEVEL ERROR RATES
Of what use are the optimal alignments? As it turns out, they are valuable for fine grain analyses: to tally and categorize the types of errors and the particular characters or interactions that are problematic in the text entry technique. The main difficulty is that we do not know which optimal alignment reflects user behaviour. In the examples, the user may have committed a deletion error and two insertion errors, as seen in the first alignment,
| Character | Count | Error Probability | |||
|---|---|---|---|---|---|
| Ins | Sub | Del | Total | ||
| q | 1 | 0 | 0 | 0 | 0 |
| u | 1 | 0 | 0 | 0 | 0 |
| i | 1 | 0 | .7500 | .2500 | 1.0000 |
| c | 1 | 0 | .7500 | 0 | .7500 |
| k | 1 | 0 | 0 | 0 | 0 |
| l | 1 | 0 | 0 | 0 | 0 |
| y | 1 | 0 | 0 | 0 | 0 |
| - | 1.25 | 1.0000 | 0 | 0 | 1.0000 |
| Total: a | 8.25 | 1.2500 | 1.5000 | 0.2500 | 3.0000 |
| Average: a | 0.1515 | 0.1818 | 0.0303 | 0.3636 | |
| a Weighted by count | |||||
The Character column contains all characters appearing along the top row of the alignments. These consist of characters in the presented text and a dash ("-"), representing an insertion. The Count column contains the count for each character, weighted by occurrences in the alignments. For example, the count for "q" is 4 / 4 = 1 because "q" appears four times in four alignments. The count for the dash is 5 / 4 = 1.25 because five insertions appear in four alignments.
The Error Probability columns are similarly computed. For the letter "i", the total error probability is 4 / 4 = 1.0 because an error occurs for each "i" in each alignment. Of the four errors, three are substitutions and one is deletion; thus, the substitution and deletion error probabilities are 3 / 4 = .75 and 1 / 4 = .25, respectively. For the letter "c", three occurrences are in error, while one is correct. Thus, the total error probability is 3 / 4 = .75. All three errors are substitution errors.
The Total row gives the total number of characters as well as the total number of errors of each type. The total number of characters is (9 + 8 + 8 + 8) / 4 = 8.25. This is the mean size of the alignments. There were three errors in total, consisting of 1.25 insertions, 1.50 substitutions, and 0.25 deletions. The values are non-integers due to the weighting factors.
The Average row gives the overall error probability for each type of error. The total error probability is 3 / 8.25 = 0.3636, for an error rate of 36.36%. This consists of 15.15% insertion errors, 18.18% substitution errors, and 3.03% deletion errors.
ERROR RATE FORUMLA
The error rate just cited (36.36%) differs slightly from the error rate given earlier using Equations 1 and 2 for the same example (37.5%). We feel the benefits afforded by the analyses described herein justify a slight correction to our earlier formula:
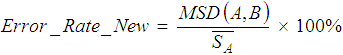
| (3) |
where ![]() is the mean size of the alignments. Equation 3 is recommended because it always yields the same error rate as
that obtained by a character-by-character analysis of the optimal alignments, as just described. In general, Equation 3 yields
a slightly lower error rate than Equation 1 since
is the mean size of the alignments. Equation 3 is recommended because it always yields the same error rate as
that obtained by a character-by-character analysis of the optimal alignments, as just described. In general, Equation 3 yields
a slightly lower error rate than Equation 1 since ![]() .
.
EXAMPLE − THREE-KEY TEXT ENTRY
We tested our character-level error analysis technique on a data set from a recent experiment [1]. The entry method uses Left (L) and Right (R) arrow keys to manoeuvre a cursor over an ordered set of characters,
_abcdefghijklmnopqrstuvwxyz
and a Select (S) key to enter a character.After each entry the cursor "snaps to home", moving to the SPACE character ("_") on the left. Thus, SPACE is entered as S, "a" as RS, "b" as RRS, "c" as RRRS, and so on. In the experiment ten participants entered text for about 25 minutes each, totalling 673 phrases of input. The mean size of the phrases was 28.3 characters. See [1] for details. Results revealed an average entry rate of about 9 wpm with just over 2% errors. Table 2 summarizes our character-level analysis of the 673 presented and transcribed phrases.
| Character | Count | Error Probability | |||
|---|---|---|---|---|---|
| Ins | Sub | Del | Total | ||
| SPACE | 2956 | 0 | 0.0027 | 0.0185 | 0.0213 |
| a | 1248 | 0 | 0.0083 | 0.0089 | 0.0172 |
| b | 231 | 0 | 0.0412 | 0.0151 | 0.0563 |
| c | 457 | 0 | 0.0241 | 0.0153 | 0.0394 |
| d | 527 | 0 | 0.0063 | 0.0127 | 0.0190 |
| e | 2051 | 0 | 0.0060 | 0.0073 | 0.0133 |
| f | 335 | 0 | 0.0119 | 0.0030 | 0.0149 |
| g | 355 | 0 | 0.0087 | 0.0047 | 0.0134 |
| h | 723 | 0 | 0.0055 | 0.0083 | 0.0138 |
| i | 1154 | 0 | 0.0117 | 0.0082 | 0.0199 |
| j | 45 | 0 | 0.0081 | 0.0141 | 0.0222 |
| k | 178 | 0 | 0.0000 | 0.0056 | 0.0056 |
| l | 647 | 0 | 0.0104 | 0.0100 | 0.0205 |
| m | 387 | 0 | 0.0129 | 0.0103 | 0.0233 |
| n | 1005 | 0 | 0.0162 | 0.0112 | 0.0274 |
| o | 1356 | 0 | 0.0156 | 0.0095 | 0.0251 |
| p | 324 | 0 | 0.0093 | 0.0031 | 0.0123 |
| q | 35 | 0 | 0.0000 | 0.0000 | 0.0000 |
| r | 1058 | 0 | 0.0112 | 0.0082 | 0.0194 |
| s | 1056 | 0 | 0.0149 | 0.0123 | 0.0271 |
| t | 1431 | 0 | 0.0054 | 0.0100 | 0.0154 |
| u | 492 | 0 | 0.0129 | 0.0094 | 0.0224 |
| v | 234 | 0 | 0.0085 | 0.0085 | 0.0171 |
| w | 293 | 0 | 0.0205 | 0.0068 | 0.0273 |
| x | 52 | 0 | 0.0000 | 0.0000 | 0.0000 |
| y | 408 | 0 | 0.0025 | 0.0025 | 0.0049 |
| z | 21 | 0 | 0.0635 | 0.0317 | 0.0952 |
| - | 41.65 | 1.0000 | 0 | 0 | 1.0000 |
| Total: a | 19100.65 | 41.6463 | 183.7073 | 199.6463 | 425 |
| Average: a | 0.00218 | 0.00962 | 0.01045 | 0.02225 | |
| a Weighted by count | |||||
The weighted average of the character error rate was 2.23%, consisting of 0.22% insertion errors, 0.96% substitution errors, and 1.05% deletion errors. The total number of characters was 19,100.65. This is the sum of the mean size of the alignments for each of the 673 phrases. As noted earlier, this value is slightly higher than the actual number of presented (19,059) or transcribed (18,901) characters.
Although Table 2 contains a variety of revealing measures, it is tedious to study. A more user-friendly rendering appears in Figure 1, showing the error rates by character, split into substitution and deletion errors. (Insertion errors are discussed later.)
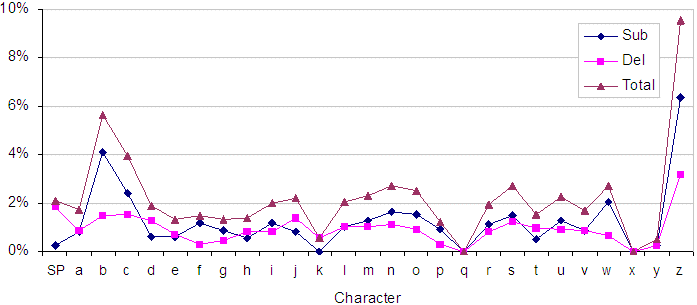
Figure 1. Substitution and deletion errors by character
CONFUSION MATRIX
In the example phrase set, the letter "o" occurred 1356 times. Most were entered correctly, however substitution errors occurred with a probability of 0.0156, or about 21.15 times. It is a simple matter to extend the error analyses to count not only the occurrences of substitution errors, but also the particular characters substituted. Data thus collected form a matrix with rows identifying presented characters and columns identifying transcribed characters. The term "confusion matrix", used in handwriting recognition, seems appropriate here.Each cell i,j in the matrix contains the number of occurrences of a substitution error where the presented character i appeared as character j in the transcribed text. As before, the counts are weighted because they are obtained by analysing the alignments, not the original presented and transcribed text strings. Figure 2 shows the results for the example data set. Note that the figure shows error counts, not probabilities.

Figure 2. Confusion matrix for three-key input data set
Deletion errors − omitting a character in the presented text − were most common. The spike at the back of Figure 2 shows deletion errors for the SPACE character. Two explanations come to mind. First, entering a SPACE requires two consecutive presses of the Select key: one to enter the preceding letter and one to enter the SPACE. Perhaps this behaviour was problematic, given the predominance of keystrokes that alternate between a cursor key and the Select key. Second, SPACE is the most common (~18%) of all the letters entered; the high error rate may simply reflect its high frequency in English text. A similar rationale may explain the small spike at the front of Figure 2, showing insertions of SPACE.
The most interesting observation in Figure 2 is the error pattern along the diagonal from front-left to back-right. This is an excellent example of the observations possible with our character-level analysis technique. For the example text entry technique, the pattern implies that errors often involve "lexical neighbours" of the desired letter. If the technique involved handwriting recognition, on the other hand, the pattern could be entirely different, showing, for example, misrecognition hot spots, where letter i is misrecognized as letter j. Such an experiment is underway, and this effect is apparent in our analyses of data collected thus far.
REFERENCES
1. MacKenzie, I. S. Mobile text entry using three keys, Proceedings of NordiCHI 2002 (to appear).2. Soukoreff, R. W., and MacKenzie, I. S. Measuring errors in text entry tasks: An application of the Levenshtein string distance statistic, Extended Abstracts of CHI 2001. New York: ACM, 2001, 319-320.