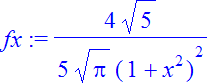FFT.html

FFT.html FFT.mws

Discrete Fourier Transform

We develop the idea of a Fourier transform in order to analyze functions in creative ways:

temporal signals in the frequency domain (signal analysis)

spatial information in the momentum domain (quantum mechanics)

For some functions the Fourier transform (FT) can be calculated analytically, but we will be mostly concerned with discrete FTs for which fast algorithms (FFTs) exist. The DFT (or FFT) is a numerical technique that can be applied to virtually any function. Many digital measuring devices (oscilloscopes) have built-in hardware which can carry out FFTs for signal analysis. In numerical analysis FFTs are used to solve ordinary and partial differential equations.

> restart; with(LinearAlgebra):

> with(plots): with(inttrans):

Warning, the name changecoords has been redefined

> fx:=(4/sqrt(5*Pi))/(1+x^2)^2;

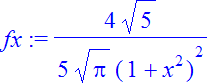> int(fx^2,x=-infinity..infinity);

> fp:=fourier(fx,x,p);

> int(fp^2,p=-infinity..infinity);

The FT defined as part of the inttrans package misses a factor, and we redefine the answer so that the norm is preserved.

The naive calculation of the FT for our function fails:

> fpn:=1/sqrt(2*Pi)*int(fx*exp(I*p*x),x=-infinity..infinity);

It can be fixed, however, by assuming that the variable p is real-valued.

> assume(p,real);

> fpn:=1/sqrt(2*Pi)*int(fx*exp(I*p*x),x=-infinity..infinity);

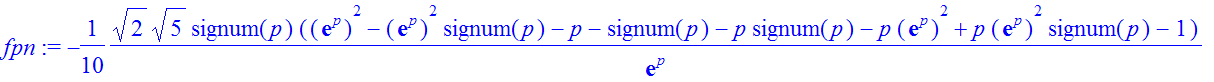> fpn:=1/sqrt(2*Pi)*int(fx*cos(p*x),x=-infinity..infinity);

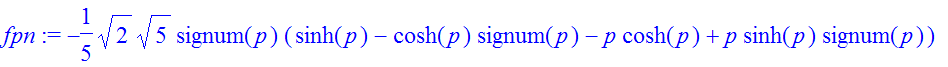> fpnI:=1/sqrt(2*Pi)*int(fx*sin(p*x),x=-infinity..infinity);

> plot([fp/sqrt(2*Pi),fpn],p=-5..5,color=[red,blue]);

The graph of the expressions is the same.

> simplify(fp/sqrt(2*Pi) - fpn);

> subs(p=3,%);

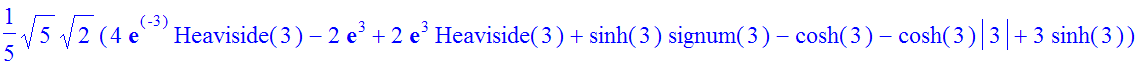> simplify(%);

Exercise 1:

Modify the above function fx in such a way as to change the scale over which it varies by replacing the 1 in the denominator by some other constant. Keep the function normalized by adjusting the factor in front of fx . Calculate the FT, and observe the relationship. Is it true that distributions fx which have more concentration at smaller x-values have transforms that emphasize more the large-p region?

> fx:=(2/Pi)^(1/4)/sqrt(a)*exp(-(x/a)^2);

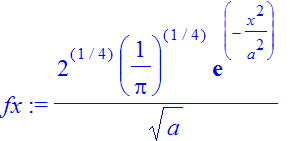> fourier(fx,x,p);

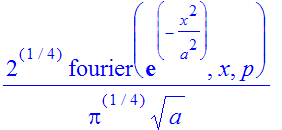> assume(a>0);

> fourier(fx,x,p);

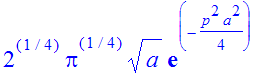The assumption on a was required for the FT to be meaningful. The example of a Gaussian is particularly illustrative, because it is obvious how the distance scale a appears as the inverse momentum scale in the FT.

Now let us look at examples relevant for signal theory:

> fourier(sin(t),t,w);

> fourier(cos(3*t),t,w);

We obtain a Dirac delta at both positive and negative frequency. For signals made up of a few frequencies the Fourier representation will be very economical:

> ft:=sin(t)+2*cos(5*t)+1/2*sin(sqrt(5)*t);

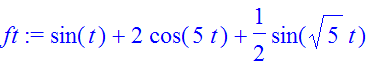> plot(ft,t=0..10);

> fourier(ft,t,w);

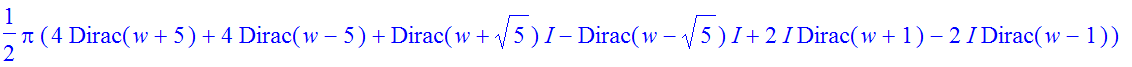Now, we can't graph the result, but in real life we never want to integrate infinite wave trains. So what happens for a finite signal?

> fw:=int(ft*exp(I*w*t),t=-20..20):

> plot([Re(fw),Im(fw)],w=-6..6,color=[red,blue]);

Clearly the information about the frequency contributions is there.

Exercise 2:

Extend the time over which the signal is integrated, i.e., consider a longer wavetrain, and graph the results. What is your observation?

Exercise 3:

Choose different signals and perform the Fourier analysis using the infinite domain, and then different finite domains.

Note how the amplitudes of the signal contributions at different frequencies in the time and frequency domains are preserved. This is a consequence of the linearity of the FT. The figure above displays also how we can generate a sequence of oscillatory functions which approximate the Dirac delta (in the limit of an infinite time domain the Dirac delta function is recovered).

Discrete Fourier Transform

In the discretized version of the FT we approximate the integral by a Riemann sum. This approximation is not unreasonable, because the integrand is assumed to be periodic, which means that the function values and derivatives at the left and right boundaries of the integration interval are equal. For this case the Riemann sum is more accurate than some of the usual quadrature rules on an equidistant grid, such as the trapezoid or Simpson rule. The reduction of the infinite domain to a finite one means that we are using a Fourier series representation instead of a true Fourier transform [investigate the worksheets FourierSeries.mws , HeatEqn.mws , WaveEqn.mws to find out more about it].

In the discrete FT we not only have a finite domain, but in fact we will discretize time and frequency (position and momentum). Let us use the position-momentum language familiar from quantum mechanics, although the same arguments apply in the time-frequency pair of variables. If we have a spatial domain of finite extent, then this implies that there is a lowest wavenumber (momentum) that can be represented (a sine wave spanning the entire domain with one positive, and one negative lobe). Likewise, when we discretize position, there will be a maximum wavenumber that can be resolved: a sequence of alternating +1, -1, can be thought of as the highest momentum wave representable for a given choice of discretization dx . Let us pick a spacing, and a number of points (which for technical reasons has to be a power of two).

> dx:=0.4; n:=8; N:=2^n;

> dp:=evalhf(2*Pi/(N*dx));

The spacing in the momentum domain follows from the arguments given above: The size of the position domain N*dx controls not only the smallest momentum that can be represented, but also the resolution in the momentum domain. The largest momentum that can be observed is given by

> p_max:=N*dp/2;

The momentum and coordinate meshes are arranged in a somewhat unusual way: we begin with the positive domains to be stored in the first halves of the arrays, followed by the negative values attached in a periodic way (following the largest positive position/momentum come the largest negative positions/momenta). We use vectors from the LinearAlgebra package for storage, but lists or arrays would work as well.

> xv:=Vector(N): pv:=Vector(N):

> for i from 1 to N do:
xv[i]:=evalhf((i-N/2-1)*dx):
if i < N/2+1 then
pv[i]:=evalhf((i-1)*dp): pv[N-i+1]:=evalhf(-i*dp): end if:
od:

> pv[20];

> pointplot({seq([i,xv[i]],i=1..N)});

> pointplot({seq([i,pv[i]],i=1..N)});

The meshes include zero as their first point. These are not the only possible choices. In particular, one can choose meshes that avoid the origin, i.e., are spaced a half-step around it, if one has reasons to avoid the origin.

Let us choose a time sequence and generate the transform. We pick a real function with sine and cosine contributions. The function is real-valued, but we prepare for a real and imaginary part yR and yI respectively.

> fx:=sin(x)+2*cos(2*x);

> yR:=Vector(N): yI:=Vector(N):

> for i from 1 to N do: yR[i]:=evalf(subs(x=xv[i],Re(fx))); yI[i]:=evalf(subs(x=xv[i],Im(fx))); od:

> plot([seq([xv[i],yR[i]],i=1..N)],style=point);

It is hard to see the signal! Choose style=line to get the idea.

> N_x:=dx*add(yR[i]^2+yI[i]^2,i=1..N);

> evalhf(FFT(n, var(yR), var(yI)));

> N_p:=dp*add(yR[i]^2+yI[i]^2,i=1..N);

This is not normalized correctly, so let us define a normalized DFT:

> yRn:=Vector(N): yIn:=Vector(N): sq:=evalf(1/sqrt(2*Pi)): for i from 1 to N do: yRn[i]:=dx*sq*yR[i]: yIn[i]:=dx*sq*yI[i]: od:

> N_p:=dp*add(yRn[i]^2+yIn[i]^2,i=1..N);

Now we understand that the FFT function carried out the sum, but did not multiply by dx (to turn it into the Riemann sum), and that it does not include the customary 1/sqrt(2*Pi) factor.

Observe the efficiency: in one GO the FFT function has calculated N integrals, one for each of the frequency (momentum) values represented on the p-mesh. The reason why it is called fast is that the effort does not scale as N^2 as would be normally expected from the DFT, but rather as N*log(N) .

Now let us graph the result:

> plot([seq([pv[i],yRn[i]],i=1..N)],style=point);

> plot([seq([pv[i],yIn[i]],i=1..N)],style=point,color=blue);

> plot([seq([pv[i],yRn[i]^2+yIn[i]^2],i=1..N)],style=point,color=black);

Evidently, unless the resolution is increased considerably one can read off the accurate weight of the different frequency contributions only when a proper lineshape is fitted to the data near the peaks: the frequency (momentum) grid can easily miss the accurate location of the peak. Nevertheless, we can see in the given example that the signal intensities for the two frequency contributions are approximately 4:1, as is appropriate for the original function fx=sin(x)+2*cos(2*x) .

Note that the frequency information is relatively sharp, because the time interval sampled contains a good number of cycles. The efficiency of the FFT to display information content in terms of population of frequencies is obvious, and this explains the widespread use of FFTs in Electronics, Acoustics, and other branches of signal processing.

There is some redundancy in the above result: We have a degree of symmetry: the real part of the FT is symmetric, while the imaginary part is antisymmetric in frequency with the end result of a symmetric intensity profile. The redundancy to some extent is the result of using a real signal only. When adding an imaginary part to the function in the time domain (at a different frequency, e.g., f=3), the real part of the transform loses its symmetry.

Exercise 4:

Play with the above code while keeping the same function: change dx , while keeping the same N ; then keep dx , while changing N . Observe the implications for the information content. If one wishes to work with a fixed total length interval, one has to use a window function to cut off the signal outside the desired time interval.

Filtering noisy data

A classical application of DFT's concerns the removal of noise from data. The idea is that noise represents signal components of high frequencies which can be removed by a low-pass filter. In this section we will construct a signal with known smooth components and will add some randomness. Then we will analyze the DFT, remove high frequencies and observe the result of an inverse transformation.

Maple has a built in random number generator for integer randoms. In the stats package there are also more sophisticated generators, but this one will suffice.

> rand()/10^12;

> evalf(rand()/10^12);

Subsequent calls result in a sequence of pseudorandom numbers. One can changed the seed value for different deterministic sequences. By dividing by 10^12 we have uniformly distributed randoms on the interval [0, 1].

> fx:=(sin(x/4)+2*cos(1/2*x));

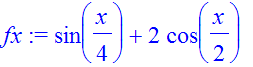> yR:=Vector(N): yI:=Vector(N):

> for i from 1 to N do: yR[i]:=evalf(subs(x=xv[i],Re(fx))+1*(rand()/10^12-0.5)); yI[i]:=evalf(subs(x=xv[i],Im(fx))); od:

> P1:=plot([seq([xv[i],yR[i]],i=1..N)],style=line): display(P1);

> evalhf(FFT(n, var(yR), var(yI)));

> plot([seq([pv[i],yR[i]],i=1..N)],style=line);

> plot([seq([pv[i],yI[i]],i=1..N)],style=line);

> p_c:=1.5;

> for i from 1 to N do: if abs(pv[i])>p_c then yR[i]:=0: yI[i]:=0: fi: od:

Now go back to the time domain using the inverse Fourier transform:

> evalhf(iFFT(n, var(yR), var(yI)));

> P2:=plot([seq([xv[i],yR[i]],i=1..N)],style=line,color=blue): display(P1,P2);

Thus, we have demonstrated low-pass filtering using a sequence of FFT/iFFT with a truncation step in the frequency domain.

Exercise 5:

Explore the results of the above filtering step by changing the cut-off frequency.

>

A quantum mechanics example

We proceed with the example of finding the DFT of a Gaussian wavepacket. The example is interesting, because we have a detailed understanding of how the wavepacket is made up of plane waves of momenta p using a Gaussian weight function defined by a center value p0 and a width dp .

>

> x0:=0; p0:=1/2; sigma:=1/4;

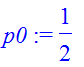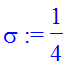> fx:=exp(-sigma^2*(x-x0)^2/2)*exp(I*p0*x)/(Pi/(sigma)^2)^(1/4);

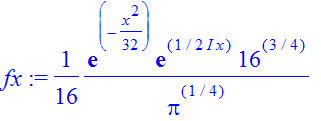> simplify(int(abs(fx)^2,x=-infinity..infinity));

The analytical FT to p-space:

> Fp:=1/sqrt(2*Pi)*int(fx*exp(-I*p*x), x=-infinity..infinity);

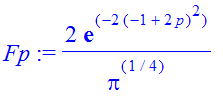The transform is real-valued, because the original function has symmetry in the real part, and anti-symmetry in the imaginary part. These combine with exp(I*p*x) in such a way as to cancel the imaginary part of the transform, since one is integrating an odd function in the imaginary part of the combined integrand.

> int(Fp^2,p=-infinity..infinity);

Now we calculate the DFT. It is advantageous to re-define the position mesh as also cut up in such a way that the array starts with small x-values followed by the wrap-around to the large negative values. This takes care of the symmetry between the coordinate and momentum representations. If one keeps the mesh used for the time-to-frequency domain conversion, an annoying phase (alternating sign) appears between adjacent points, and a wrong imaginary part is calculated. This makes it difficult to interpret the results.

> dx:=0.4; n:=8; N:=2^n;

> dp:=evalhf(2*Pi/(N*dx));

> p_max:=N*dp/2;

> xv:=Vector(N): pv:=Vector(N):

> for i from 1 to N do:
if i < N/2+1 then
xv[i]:=evalhf((i-1)*dx): xv[N-i+1]:=evalhf(-i*dx):
pv[i]:=evalhf((i-1)*dp): pv[N-i+1]:=evalhf(-i*dp): end if:
od:

> pv[20];

> pointplot({seq([i,xv[i]],i=1..N)});

> pointplot({seq([i,pv[i]],i=1..N)});

> yR:=Vector(N): yI:=Vector(N):

> for i from 1 to N do: yR[i]:=evalf(subs(x=xv[i],Re(fx))); yI[i]:=evalf(subs(x=xv[i],Im(fx))); od:

> plot([seq([xv[i],yR[i]],i=1..N)],style=point);

> plot([seq([xv[i],yI[i]],i=1..N)],style=point,color=blue);

> N_x:=dx*add(yR[i]^2+yI[i]^2,i=1..N);

> evalhf(FFT(n, var(yR), var(yI)));

> N_p:=dp*add(yR[i]^2+yI[i]^2,i=1..N);

This is not normalized correctly, so let us define a normalized DFT:

> yRn:=Vector(N): yIn:=Vector(N): sq:=evalf(1/sqrt(2*Pi)): for i from 1 to N do: yRn[i]:=dx*sq*yR[i]: yIn[i]:=dx*sq*yI[i]: od:

> N_p:=dp*add(yRn[i]^2+yIn[i]^2,i=1..N);

> plot([seq([pv[i],yRn[i]],i=1..N)],style=point);

> plot([seq([pv[i],yIn[i]],i=1..N)],style=point,color=blue);

The imaginary part is returned as zero, while the real part describes a wavefunction of Gaussian shape centered on p0.

Exercise 6:

Change the parameters of the Gaussian wavepacket and observe how they are reflected in the DFT results.

As a final check we carry out an error analysis: we do have an analytic answer for the FT, i.e., we can figure out how accurate the DFT is for the present example. Let us evaluate the analytic FT at the grid points:

> FT:=Vector(N): for i from 1 to N do: FT[i]:=evalf(subs(p= pv[i],Fp), 16); od:

Pick a location on the momentum mesh and compare the results and calculate the relative error:

> i0:=10: pv[i0];

> FT[i0],yRn[i0],abs((FT[i0]-yRn[i0])/FT[i0]);

Phenomenal! The agreement is with computational accuracy for the analytic result controlled by the Digits variable; (increase Digits and repeat the calculation to confirm this).

However, if we go to larger momenta:

> i0:=30: pv[i0];

> FT[i0],yRn[i0],abs((FT[i0]-yRn[i0])/FT[i0]);

In fact, if one calculates the average relative error over the entire mesh one obtains:

> add(abs((FT[i]-yRn[i])/FT[i]),i=1..N)/N;

A ridiculously large number! This is the result of applying periodic boundary conditions in the DFT. Instead of falling to zero the 'Gaussian' as computed per DFT connects periodically to the neighbours in adjacent cells.

> P1:=plot([seq([pv[i],log(yRn[i])],i=1..N/2)]):

> P2:=plot([seq([pv[i],log(FT[i])],i=1..N/2)],color=blue):

> display([P1,P2],view=[0..4,-25..1]);

Exercise 7:

Compare the analytic and numerical FT for different choices of parameteres, particularly for smaller grid sizes.

Exercise 8:

Carry out the comparison between analytic and discrete FT for a wavepacket of a different shape, namely a Lorentzian.

exp(I*p0*x)*a^2/(a^2+(x-x0)^2) . Why are the results less accurate than for a Gaussian?

>