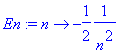MappedFourierGrid.html

MappedFourierGrid.html MappedFourierGrid.mws

The mapped Fourier grid method for the Coulomb problem

E.Fattal, R. Baer, R. Kosloff, Phys. Rev. E 53 , 1217 (1996); F. Brau, C. Semay, J. Comp. Phys. 139 , 127 (1998); V. Kokouline, O. Dulieu, R. Kosloff, F. Masnou-Seeuws, J. Chem. Phys. 110 , 9865 (1999) for implementation details. The Fourier grid method itself goes back to the pioneering work of R. Meyer, J. Chem. Phys. 52 , 2053 (1970).

In fact, some of the references by Kosloff et al are confusing the issues as to what basis is used. The work is in coordinate space in a position eigenstate basis (a Kronecker delta basis, which has the right limit as dx is sent to zero, i.e., the basis function is a Kronecker divided by dx , with the assumption that x_j=j*dx . Important implementation details concern questions like: even or odd number of grid points, and whether the entire x -axis or only the x>0 region are used in the problem. The Fourier grid method makes use of the fact that the Fourier transform of the Kronecker delta function is known as a plane wave in p -space. This permits a direct calculation of kinetic energy matrix elements in coordinate representation as a non-diagonal matrix. The potential matrix is, of course, calculated as a diagonal matrix with no matrix elements to be evaluated. For some Fourier grids the kinetic energy matrix can be calculated in closed form (cf. R. Meyer).

Our work here uses a mix of methods from the above references. It implements the Fourier-sine representation on the (0,Pi) interval. This then corresponds really to a Fourier series expansion which is close in spirit to the original work of Meyer, and also to the more recent work of Brau and Semay. It has a drawback in that we do not have a closed-form expression for the kinetic energy matrix. On the other hand the matrix can be calculated once and stored, and then re-used for many applications. Its computation cost will become only considerable for very large grids. The advantage of the method is that it makes use of a pure sine expansion, i.e., the symmetry of the radial problem is implemented directly. In order to attack Coulomb-type problems we then implement a mapping along the lines of the first reference, i.e., the work of Kosloff et al with a further adaptation in order to connect to the (0,Pi) interval. At first, we demonstrate, however, the virtues of the mapping as presented in that work.

The rectangular Fourier grid is not working well for problems in which there is a correlation between position and momentum variables, such as in the Coulomb problem: small r corresponds to high p , while large r corresponds to small p . The singularities in the potential in both r and p space are responsible for an inadequacy of the rectangular Fourier grid. The idea behind the mapping is to use the classical phase space region as a guide. For a given energy E=H(r,p) the classically allowed region maps out a volume in phase space. The wave function for a bound state will decrease exponentially beyond this regime. The idea is to apply a canonical transformation from (p,q=r) into (P,Q) , and to employ a rectangular grid in (P,Q) . Our objective is to demonstrate that a good approximation to the bound-state spectrum can be obtained when using a Fourier collocation method in the (P,Q) variables.

> restart; with(LinearAlgebra): with(plots):

Warning, the name changecoords has been redefined

Let us demonstrate the problem by contour diagrams for classical energies of some Rydberg levels. Atomic units (hbar=m_e=e=1) are used.

> En:=n->-1/(2*n^2);

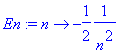> Hpq:=p^2/2-1/q;

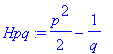> contourplot(Hpq,q=-0..100,p=-1..1,levels=[En(1),En(2),En(3),En(4),En(5)],numpoints=10000,filled=true);

Kosloff et al. make the point about the missing classical phase space volume at large momenta and small r. One might think that this is not all that relevant for the quantum problem, because much of this space is inaccessible in quantum mechanics due to the zero-point motion, but it turns out to be important. In any case, the picture shows dramatically that a rectangular region in the (q,p) variables with q=r is very inefficient. Therefore, the objective is to optimize the calculation by filling the classically accessible region with a rectangular region in a mapped variable. Kosloff et al make use of an arctan transformation (which we have used in different form with finite-difference methods, e.g., J. Phys. B 17 , 2591 and Phys. Rev. A 44 , R5346).

> beta:=2.5E-4; A:=3999.9;

> rM:=Q->Q-A*arctan(beta*Q);

> plot(rM(Q),Q=0..5000);

An equidistant mesh in Q will concentrate may points at small r .

One needs to calculate the transformation. For a single-variable map we have:

> beta:='beta': A:='A': J:=diff(rM(Q),Q);

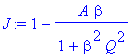The Hamiltonian then simply becomes:

> HPQ:=P^2/(2*J^2)-1/rM(Q);

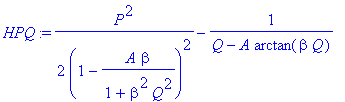Re-introduce the numerical values for the mapping parameters:

> beta:=2.5E-4; A:=3999.9;

> contourplot(HPQ,Q=-200..1500,P=-0.02..0.02,levels=[En(1),En(2),En(3),En(4),En(5)],numpoints=10000,filled=true);

The remap of the variables (canonical transformation) from (q,p) to (Q,P) leads to a rectangular area in which one has not only good efficiency in terms of coverage of the classically accessible region, but, in fact, also enclosure of that region which was not possible in (q,p) with the same amount of effort. The diagrams are similar to Figs. 3,4 in the reference.

Now we are armed to proceed with the spectrum calculation. The kinetic energy in the transformed variables is a function of P and Q . Therefore, one has to figure out a proper way of how to deal with it, i.e., whether one should use P/J(Q) as an operator and square it, or whether P^2/J(Q)^2 can be carried out in sequence. In any case, we do not have a multiplicative operator in P -space for the kinetic energy. Meyer has included the possibility of such a kinetic energy operator in his work.

We are seeking a matrix representation of the Hamiltonian which we will then diagonalize. In order to avoid trouble with the periodic boundary conditions implied in the Fourier method we discretize the [-L,L] interval and look for anti-symmetric eigenfunctions. The first reference provides some hints, but no details in this respect.

> restart; with(LinearAlgebra): Digits:=14:

> n:=6; N:=2^n;

> dQ:=100;

> dP:=evalf(Pi/(N*dQ));

> P_max:=N/2*dP;

These parameter settings provide a rectangular area that can be identified in the above diagram.

Perhaps we should first demonstrate how poorly the regular Fourier grid method does. In this case we choose:

> dq:=0.5;

> dp:=evalf(Pi/(N*dq));

> p_max:=N/2*dp;

Construct the kinetic energy matrix in coordinate representation using the fact that it is diagonal in p space, i.e., by inserting plane-wave completeness relations approximated by their truncated versions.

> TM:=Matrix(N,N):

> L:=N*dq;

> BF:=(k,j)->sqrt(2/N)*sin(Pi*k*j/N);

> simplify(add(BF(1,j)*BF(1,j),j=1..N));

> simplify(add(BF(1,j)*BF(2,j),j=1..N));

This serves as a check that the basis is orthonormal. Try some other values of k to verify.

The kinetic energy matrix is easy to assemble now: we have a basis of Kronecker deltas <x_i|j> = KND(i,j)/dx . The Fourier series amplitudes of these functions are the basis functions <p_k|j> = BF(k,j) for which we know the momentum eigenvalues, and therefore the kinetic energies as 1/2*(Pi*k/L)^2 . One way to prove it is to differentiate the basis function BF(k,j) twice with respect to x after replacing j*dq by x , which with the definition L=N*dq brings out a -(Pi*k/L)^2 factor, and then to multiply by (-1/2) in atomic units.

This is implemented below:

> for j from 1 to N do: for jp from 1 to N do: TM[jp,j]:=evalf(add(BF(k,j)*BF(k,jp)*(Pi*k/L)^2/2,k=1..N)); od: od:

> TM[1,1],TM[1,2],TM[2,1];

It looks like the matrix is symmetric, which shouldn't be a surprise.

Now let us add a potential matrix: fortunately we avoid the origin in our mesh and circumvent the Coulomb singularity.

> for j from 1 to N do: TM[j,j]:=TM[j,j]-1/(j*dq); od:

> EV:=Eigenvalues(TM):

> EV[1],EV[2];

> EV0:=sort([seq(Re(EV[n]),n=1..N)]);

This method results in not so good eigenvalues when compared to -0.5/n^2 . They look like upper bounds, but seem to reflect a bad coverage of the classically accessible phase space region.

Exercise 1:

Choose different values of the dq spacing and observe the dependence of the low-lying eigenvalues (the lowest bound states). Then increase the number of points and record the improvement for given choices of dq .

How do we implement the idea in PQ space? The momentum operator P is given as -I*1/J(Q) * d/dQ , which means that we have to implement -0.5/J(Q)*d/dQ 1/J(Q) d/dQ as kinetic energy operator. We will follow two approaches: first, we implement this directly; then we follow an idea implemented by Kokoouline et al to construct a symmetric matrix after transforming the wavefunction. The second method appears to be somewhat less efficient than the first one, although some savings can be obtained from using a simplified matrix diagonalization.

>

> restart; with(LinearAlgebra): Digits:=14:

> N:=20;

> dx:=evalf(Pi/(N+1));

We supplement the Kosloff mapping with a scale transfo (using the parameter s0 ) to map from the interval (0,Pi) for x into a Q range, then into r

according to r = s0*x-A*arctan(beta*s0*x)

We need to assemble sine-sine and sine-cosine matrices with k^2 and k factors respectively. This follows from the observation that the kinetic energy operator now has both first and second derivatives, i.e., d/dQ and d^2/dQ^2 . The first derivative turns the sine-basis function into a cosine times k . We pre-assemble the matrices, and then we can use them for calculations with differently scaled variables.

> CSM:=Matrix(N,N): SSM:=Matrix(N,N):

We do not include the - sign, because we want -1/2 times the second derivative anyway, and therefore we skip the factor 2 as well! Rather than defining the basis function as done in the previous section we work with sines and incorporate the normalization by correcting the sums by a 2/(N+1) factor.

> for i from 1 to N do: for j from 1 to N do: SSM[i,j]:=evalf(1/(N+1)*add(k^2*sin(k*j*dx)*sin(k*i*dx),k=1..N)): CSM[i,j]:=evalf(1/(N+1)*add(k*sin(k*j*dx)*cos(k*i*dx),k=1..N)): od: od:

> CSM[2,1],CSM[2,2],CSM[1,2];

> SSM[2,1],SSM[2,2],SSM[1,2];

The latter matrix is no longer symmetric. This can pose a problem for efficiency in matrix diagonalization.

From these pre-computed matrices we can assemble the Hamiltonian matrix following a choice of parameters.

> r:=x->s0*x-A*arctan(beta*s0*x);

> J:=D(r);

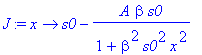> Jp:=D(J);

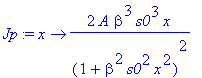We include the possibility of non-zero angular momentum, i.e., we define a centrifugal potential.

> L:=0; Vcf:=x->L*(L+1)/2/r(x)^2;

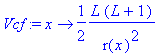> A:=3999.9: beta:=0.00025:

In order to map the (0,Pi) interval to a large Q range (as is required according to the graph in the first section) we choose a large scale factor s0 :

> s0:=500;

> HM:=Matrix(N,N):

Note that the Jacobian factors that follow from 1/J(Q) and simply multiply the derivative matrices that are computed in momentum representation (or in trig representation). The differential operator is given for F(Q)=1/J(Q) as F(Q)*F'(Q)*d/dQ - F(Q)^2*d^2/dQ^2 .

> for i from 1 to N do: f1:=Jp(i*dx): f2:=1/J(i*dx): for j from 1 to N do: HM[i,j]:=(CSM[i,j]*f1*f2 + SSM[i,j])*f2^2: od: HM[i,i]:=HM[i,i]+evalf(-1/r(i*dx)+Vcf(i*dx)): od:

> EV:=Eigenvalues(HM);

> EV[1];

> convert(EV,list);

> EVs:=sort(map(Re,%));

We have excellent results for a number of eigenenergies!

Exercise 2:

Explore the error (absolute and relative) of the lowest 10 eigenvalues by comparing with -0.5/n^2 . Then increase the angular momentum quantum number from L=0 to non-zero calues and observe how it agrees (note that the spectrum then starts at n=L ).

The next question concerns the eigenvectors. We need to sort the spectrum, i.e., put the eigenvectors as computed in Maple in an order that corresponds to the order n=1,2,3...

> VE:=Eigenvectors(HM,output='list'):

> Vp:=[seq([Re(VE[i][1]),VE[i][2],map(Re,VE[i][3])],i=1..nops(VE))]:

> Min:=proc(x,y); if type(x,numeric) and type(y,numeric) then if x<=y then RETURN(true): else RETURN(false): fi; elif type(x,list) and type(y,list) and type(x[1],numeric) and type(y[1],numeric) then if x[1]<=y[1] then RETURN(true): else RETURN(false): fi; elif convert(x,string)<=convert(y,string) then RETURN(true): else RETURN(false): fi: end:

> VEs:=sort(Vp,Min):

> n_sel:=2; VEs[n_sel];

Let us look at the eigenvector as a function of the radial coordinate r(i*dx) :

> plot([seq([r(i*dx),VEs[n_sel][3][i]],i=1..N)]);

How can we interpolate the functions? This is accomplished using the sinc function according to the Shannon theorem.

> sinc:=x->sin(x)/x;

> fE:=n->evalf(add(VEs[n][3][i]*sinc(Pi/dx*(x-i*dx)),i=1..N));

We display the lowest five states as a function of the variable 0 < x < Pi . We graph their densities, and keep in mind that these are radial densities:

> plot([seq(fE(i)^2,i=1..5)],x=0..3.14,color=[red,blue,green,black,magenta]);

The results are smooth.

Now we want to see them as a function of r , and to compare them with the real thing! A parametric plot allows to have a look:

> plot([seq([r(x),fE(i)^2,x=0..3.14],i=1..5)],color=[red,blue,green,black,magenta],view=[0..30,0..0.5]);

Evidently the orbitals are not normalized consistently. The area under the curves was consistent from orbital to orbital when looked at as a function of x , but clearly not so as a function of r . Thus, we need to compute normalization constants if we wish to compare with the exact functions.

The constants can be calculated by summing over x , but the Jacobian has to be included. In this way the r-integral is reduced to an integral over x according to dr=J(x)dx .

> Dx:=evalf(Pi/31): Nc:=evalf(Dx*add(subs(x=i*Dx,fE(1)^2*J(x)),i=1..30));

> P1:=plot([r(x),-1/sqrt(Nc)*fE(1),x=0..3.14],color=red,view=[0..10,0..0.8]):

> int(4*r^2*exp(-2*r),r=0..infinity);

> P1e:=plot(2*r*exp(-r),r=0..10,color=blue):

> plots[display](P1,P1e);

It is hard to distinguish the two, so we can graph the relative error:

> plot([r(x),2*r(x)*exp(-r(x))+1/sqrt(Nc)*fE(1),x=0..3.14],color=red,view=[0..10,-0.0002..0.0002]);

Exercise 3:

Investigate the relative error for other low-lying eigenstates. You will need to define the radial functions for these states. Investigate how a change in the scale parameter s0 affects the accuracy of individual eigenenergies and eigenfunctions.

Next we implement a method to obtain a symmetric Hamiltonian matrix as presented in the work of Kokoouline et al. The first steps are similar to the previous section:

> restart; with(LinearAlgebra): Digits:=14:

> N:=20;

> dx:=evalf(Pi/(N+1));

We need only a second-derivative matrix:

> SSM:=Matrix(N,N):

> for i from 1 to N do: for j from 1 to N do: SSM[i,j]:=evalf(1/(N+1)*add(k^2*sin(k*j*dx)*sin(k*i*dx),k=1..N)): od: od:

> SSM[2,1],SSM[2,2],SSM[1,2];

This matrix is symmetric. We avoid first derivatives.

The scale transformation is used as before:

> r:=x->s0*x-A*arctan(beta*s0*x);

> J:=D(r);

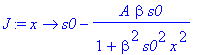> Jp:=D(J);

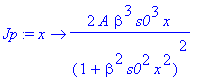> Jpp:=D(Jp);

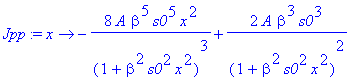The diagonal multiplicative terms of the kinetic energy matrix are collected in an effective potential function. The wavefunction Psi(Q) has been scaled into Phi(Q)/sqrt(J(Q))

> Vc:=x->7/8*(Jp(x)/J(x)^2)^2-Jpp(x)/4/J(x)^3;

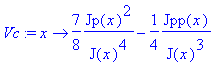> A:=3999.9: beta:=0.00025:

> s0:=800;

> HM:=Matrix(N,N):

> L:=0: Vcf:=x->L*(L+1)/2/r(x)^2;

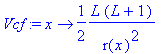> for i from 1 to N do: f2:=1/J(i*dx): for j from 1 to N do: HM[i,j]:=SSM[i,j]*(f2^2+1/J(j*dx)^2)/2: od: HM[i,i]:=HM[i,i]-evalf(1/r(i*dx)-Vcf(i*dx)-Vc(i*dx)): od:

> HM[1,2],HM[2,1],HM[2,2];

> EV:=Eigenvalues(HM);

> EV[1];

> EVs:=sort(map(Re,convert(EV,list)));

> Eh:=n->evalf(-1/2/n^2);

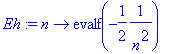> seq(Eh(i+L)-EVs[i],i=1..20);

Depending on the choice of s0 we can reduce the error for either the lowest eigenvalues or for some intermediate ones. It appears, however, as if the solution of the resulting symmetric eigenvalue problem is harder than the solution of the original non-symmetric problem, i.e., the convergence is not as fast. It is harder to converge on the low-lying states - this may be a price to be paid for scaling away the wavefunction with 1/sqrt(J) .

Exercise 4:

Change the Coulomb potential to a screened Coulomb potential form (e.g., an appropriate potential for Helium singlet structure as used in AtomicModel.mws) and compare the efficiency of the methods of the last two sections in obtaining eigenenergy spectra for the L=0,1,2 sectors.

>