� Taylor expansion of an operator product �
��
�� We check the order of the split-operator time propagation technique. First, we analyze a popular version of the time splitting technique (used in Ehrenfest.mws). Then, we show why the simple operator product � exp(-I*(T+V)*dt) = exp(-I*T*dt) exp(-I*V*dt) � results in an � O(dt^2) � error if � T � and � V � do not commute. Then, we analyze an � O(dt^4) � accurate scheme which involves a large amount of algebraic computations. �
��
�� This is, of course, related to the Campbell-Baker-Hausdorff formula, which reads ([A,B] : = A B - B A): �
�� exp(A) exp(B) = exp(O), where O = A + B + 1/2 [A,B] + 1/12 ([[A,B],B] + [A,[A,B]]) + ... �
��
�� This worksheet can be used in maple6 and maple7, but it gobbles lots of memory there. It works fine in maple8. �
��
| > | �restart; � |
�
| > | �unassign(`&*`); � define(`&*`,multilinear,zero=0,identity=1,flat); � � |
�
| > | �A&*B; � |
�
![]() �
�
�
| > | �a&*A; � |
�
![]() �
�
�
| > | �gamma &* A; � |
�
![]() �
�
� If we need a variable to be treated as a constant, we add it to the list: �
��
| > | �constants:=constants,dt; � |
�
![]() �
�
�
| > | �&*(A,dt,B); � |
�
![]() �
�
�
| > | �simplify(%); � |
�
![]() �
�
�
| > | �taylor(exp(-I*A&*B*dt),dt=0,3); � |
�
Error, (in series/fracpower) unable to compute series
�
�
� Setting � dt � to a constant is problematic, can't Taylor expand about it. So the trick is to Taylor expand about a variable ( � h � in our case), and later to make substitutions, so that one may make use of the constant property. The above Taylor expansion attempt failed, because we can't expand about a variable that has just been declared to be a constant. �
��
| > | �taylor(exp(-I*A&*B*h),h=0,3); � |
�
![]() �
�
�
| > | �subs(h=dt,%); � |
�
![]() �
�
�
| > | �No:=5; #order to which we expand � |
�
![]() �
�
�
| > | �Ut:=convert(taylor(exp(-I*(A+B)*h),h=0,No),polynom); � |
�
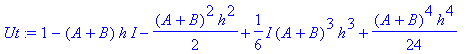 �
�
� We need to do something here: if we leave it as is, the powers of � A,B � get evaluated assuming a commutative product. �
��
| > | �Ut:=subs((A+B)^2=(A+B)&*(A+B),(A+B)^3=(A+B)&*(A+B)&*(A+B),(A+B)^4=(A+B)&*(A+B)&*(A+B)&*(A+B),Ut); � |
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
�
| > | �UtA:=convert(taylor(exp(-I*(A)*h/2),h=0,No),polynom); � |
�
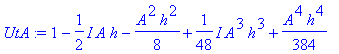 �
�
�
| > | �UtB:=convert(taylor(exp(-I*(B)*h),h=0,No),polynom); � |
�
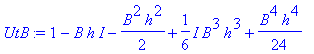 �
�
�
| > | �Uspo:=simplify(subs(h=dt,UtA &* UtB &* UtA)); � |
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
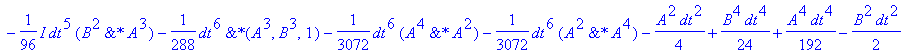 �
�
![]() �
�
![]() �
�
�
| > | �Udif:=simplify(subs(h=dt,Ut)-Uspo); � |
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
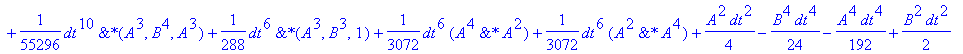 �
�
![]() �
�
![]() �
�
�
| > | �coeff(Udif,dt,0),coeff(Udif,dt,1); � |
�
![]() �
�
�
| > | �C2:=coeff(Udif,dt,2); � |
�
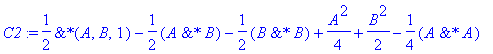 �
�
�
| > | �C3:=coeff(Udif,dt,3); � |
�
![]() �
�
![]() �
�
�
| > | �C4:=coeff(Udif,dt,4); � |
�
![]() �
�
![]() �
�
![]() �
�
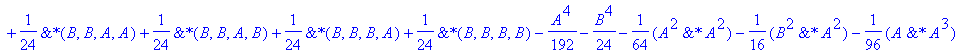 �
�
�
| > | �simplify(C2); � |
�
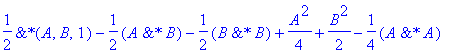 �
�
�
| > | �definemore(`&*`, � &*(1,A::symbol,B::symbol)=A&*B,&*(A::symbol,1,B::symbol)=A&*B,&*(A::symbol,B::symbol,1)=A&*B); � � |
�
| > | �simplify(C2); � |
�
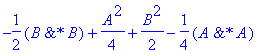 �
�
�
| > | �definemore(`&*`,&*(B::symbol,B::symbol) = B^2); � |
� This one was tricky, some other obvious versions didn't work (putting in the � ::symbol � was essential)! �
��
| > | �simplify(A &* A); � |
�
![]() �
�
�
| > | �simplify(C2); � |
�
![]() �
�
�
| > | �simplify(C3); � |
�
![]() �
�
![]() �
�
� Will this vanish? Make sure the original expansions are to sufficient order! �
��
�� Note that obvious simplifications were not carried out! Such as � &*(A,B^2,1) = A &* B^2 � , despite the formal prescription. Why? �
��
| > | �whattype(B^2); � |
�
![]() �
�
�
| > | �definemore(`&*`, � &*(1,A::algebraic,B::algebraic)=A&*B,&*(A::algebraic,1,B::algebraic)=A&*B,&*(A::algebraic,B::algebraic,1)=A&*B); � � |
�
| > | �simplify(C3); � |
�
![]() �
�
![]() �
�
� OK, so we managed to get the triple product reduced when a constant (1) is inside, while a power of operators appears. �
��
| > | �definemore(`&*`, � &*(A::algebraic,A::algebraic,B::algebraic)=&*(A^2,B),&*(A::algebraic,B::algebraic,B::algebraic)=&*(A,B^2)); � |
�
| > | �simplify(C3); � |
�
![]() �
�
![]() �
�
�
| > | �definemore(`&*`, � &*(A::algebraic,A::algebraic,A::algebraic)=A^3,&*(A::algebraic,(A::algebraic)^2)=A^3,&*((A::algebraic)^2,A::algebraic)=A^3); � |
�
| > | �simplify(C3); � |
�
![]() �
�
� The third-order error term can be expressed in terms of commutators: �
��
| > | �CM:=(A,B)->A &* B-B &* A; � |
�
![]() �
�
�
| > | �C3f:=I*(CM(A+2*B,CM(A,B)))/24; � |
�
![]() �
�
�
| > | �simplify(C3-C3f); � |
�
![]() �
�
�
| > | �
� Now show that this is better than the naive splitting: �
��
| > | �UtA:=convert(taylor(exp(-I*(A)*h),h=0,No),polynom); � |
�
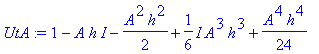 �
�
�
| > | �UtB:=convert(taylor(exp(-I*(B)*h),h=0,No),polynom); � |
�
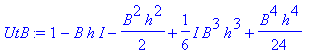 �
�
�
| > | �Uspo:=simplify(subs(h=dt,UtA &* UtB)); � |
�
![]() �
�
![]() �
�
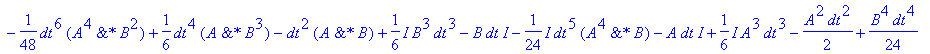 �
�
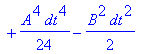 �
�
�
| > | �Udif:=simplify(subs(h=dt,Ut)-Uspo); � |
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
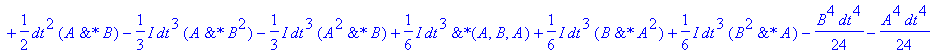 �
�
![]() �
�
�
| > | �coeff(Udif,dt,0),coeff(Udif,dt,1); � |
�
![]() �
�
�
| > | �C2:=coeff(Udif,dt,2); � |
�
![]() �
�
� The simple product is only second-order accurate, i.e., an � O(dt^2) � term survive if � A � and � B � don't commute. �
��
�� Exercise: �
�� Look at the Campbell-Baker-Hausdorff expansion with a smallness parameter dt to generate a Taylor series. �
�� exp(A*dt) exp(B*dt) = exp(O*dt) � , where � O = A + B + 1/2 [A,B] + 1/12 ([[A,B],B] + [A,[A,B]]) + ... �
�� Use the Taylor expansion to verify the quoted result, and calculate the next order, i.e., the � O(dt^3) � expression. �
��
�� The next issue: can we generate a more complicated split-operator technique which will agree with the exact answer to a higher order in dt? �
�� The answer is yes. We first define the basic split-operator technique as a single step: �
�� U2 = exp(-I*A*dt/2) exp(-I*B*dt) exp(-I*A*dt/2) � as a function of � A, B, dt �
�� U3 = U2(A,B,g*dt) U2(A,B,(1-2*g)*dt) U2(A,B,g*t) � will work for a particular choice of � g � . �
��
| > | �U2:=(A,B,h)->exp(-I*h/2*A) &* exp(-I*h*B) &* exp(-I*h/2*A); � |
�
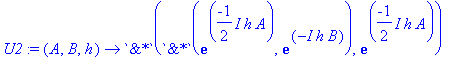 �
�
�
| > | �g:='g': # a parameter to subdivide the time step dt to be optimized. � |
�
| > | �U3:=U2(A,B,g*h) &* U2(A,B,(1-2*g)*h) &* U2(A,B,g*h); � |
�
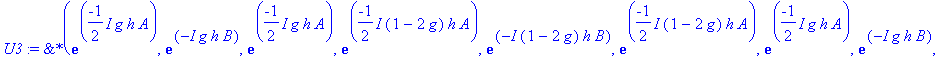 �
�
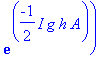 �
�
�
| > | �convert(taylor(U3,h=0,No),polynom); � |
�
Error, (in D/procedure) index out of range: function takes only 0 arguments
�
�
� The direct approach won't work. We need to do what was done before, namely generate the Taylor expansions for the individual pieces, and put them together. �
��
| > | �UtA:=convert(taylor(exp(-I*(A)*h/2),h=0,No),polynom); � |
�
| > | �UtB:=convert(taylor(exp(-I*(B)*h),h=0,No),polynom); � |
�
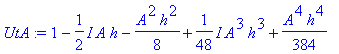 �
�
�
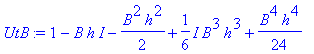 �
�
�
| > | �U2:=unapply(UtA &* UtB &* UtA, A,B,h): � |
� The naive implementation is given below. �
��
| > | �# U3:=U2(A,B,g*h) &* U2(A,B,(1-2*g)*h) &* U2(A,B,g*h): � |
�
| > | �constants:=constants,g; � |
�
![]() �
�
�
| > | �#U3:=simplify( subs(h=dt,U2(A,B,g*h) &* U2(A,B,(1-2*g)*h) &* U2(A,B,g*h)) ): � |
� The above line would at least make use of the fact that � dt � is a constant, and simplify operator products. It is, however, too cumbersome for Maple to evaluate within a reasonable amount of memory and time. The trick is to build up the expression gradually, and to keep only the lowest four orders in � dt � for each factor as one builds the expression. Note that back-and-forth substitutions � dt � vs � h � are needed. Taylor expansion will work with � h � , and not with � dt � . Non-commutative product simplification requires � dt � , so that it is recognized as a constant. �
��
| > | �U3a:=convert(taylor(subs(dt=h,simplify(subs(h=dt,U2(A,B,g*h)))),h=0,No),polynom); � |
�
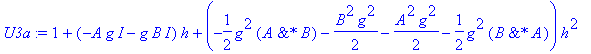 �
�
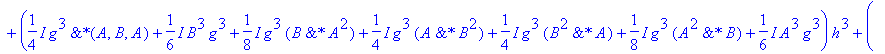 �
�
![]() �
�
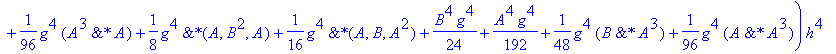 �
�
�
| > | �U3b:=convert(taylor(subs(dt=h,simplify(subs(h=dt,U2(A,B,(1-2*g)*h)))),h=0,No),polynom); � |
�
![]() �
�
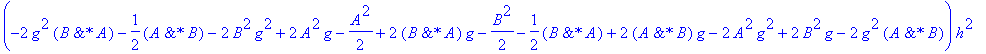 �
�
![]() �
�
![]() �
�
![]() �
�
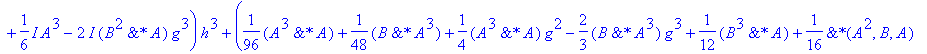 �
�
![]() �
�
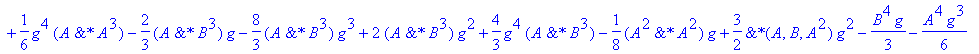 �
�
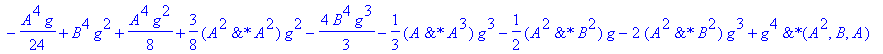 �
�
![]() �
�
![]() �
�
![]() �
�
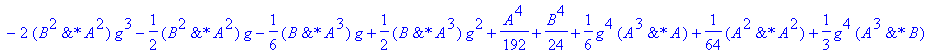 �
�
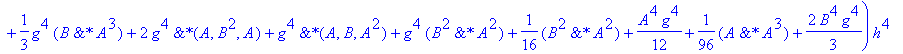 �
�
�
| > | �U3p:= expand(subs(h=dt,U3a) &* subs(h=dt,U3b) ): � |
�
| > | �U3p:=convert(taylor(subs(dt=h,U3p),h=0,No),polynom): � |
�
| > | �U3p:= expand(subs(h=dt,U3p) &* subs(h=dt, U3a)): � |
�
| > | �U3:=convert(taylor(subs(dt=h,U3p),h=0,No),polynom): � |
� Note that this relatively fast computation relies on the Taylor truncations. Try it without them and see memory and time gobbled up. �
��
| > | �coeff(U3,h,1); � |
�
![]() �
�
�
| > | �Ut; � |
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
� Now we verify that the time evolution operator expressions agree in their orders 0 to 2: �
��
| > | �DIF:=simplify(Ut-U3): � |
�
| > | �coeff(DIF,h,0); � |
�
![]() �
�
�
| > | �coeff(DIF,h,1); � |
�
![]() �
�
�
| > | �coeff(DIF,h,2); � |
�
![]() �
�
�
| > | �DIF3:=coeff(DIF,h,3); � |
�
![]() �
�
![]() �
�
![]() �
�
![]() �
�
� Now show that a particular choice of � g � turns this into zero: �
��
| > | �simplify(subs(g=1/(2-2^(1/3)),DIF3)); � |
�
![]() �
�
� This completes the proof that a fourth-order accurate time evolution operator can be found. �
�� In the numerical implementation one needs to ask the question whether this algorithm is economical. The improved accuracy comes at the price of a substantial number of additional calculations. �
��
| > | �
�
| > | �
�
| > | �