TippyTop.mws
Tippy Top
The tippy-top (or British: tippe top) has fascinated physicists for quite some time. It represents a good computational physics problem due to the fascinating motion, as well as due to the fact that analytically it is not easy to make progress on the problem. A good recipe for numerical work appeared in an article by Richard J. Cohen in American Journal of Physics (AJP 45, 12 (1977)). It did not emphasize the previous attempts at establishing whether there are conserved quantities in this problem. The latter are essential at understanding the spherical top's remarkable behaviour.
What is a tippy top? Think of a sphere which has an axially symmetric mass distribution (such that a rotor axis is defined with associated moment of inertia I3), but whose center of gravity is not at the center of the sphere. This can be accomplished by making the sphere out of two parts of different mass density, or by cutting off the sphere and introducing a stem. In the latter version wooden tippy tops are sold in toy stores, and they resemble mushrooms. What is remarkable about such a top? When one twists the top at the stem and puts it down on a not too smooth surface with the stem straight up (polar angle
theta=0
), it begins after a second or so to precess and nutate, i.e., the stem leaves the vertical position, and provided the top was spun fast enough it will move towards the
theta=Pi
position and continue spinning on its stem. For the mathematical details that follow Cohen's article, and then go a bit beyond look at the included lecture notes (jpg-files).
Why are physicists so fascinated by the tippy top? Cohen reprints a picture of Nobel laureates Niels Bohr and Wolfgang Pauli playing with this toy. There are several reasons for this. First of all, experienced mechanics afficionados have played with normal tops, and have learned about them in textbooks. They certainly know about the weird effects, how the gravitational torque makes these precess rather then fall when the tops are spinning. They know from introductory texts (e.g., Feynman lectures) how to think about the conservation properties, how the angular momentum vector keeps its magnitude approximately constant and revolves about the suspension point. Friction forces play a minor role, because the precessional angular velocity is small, but they are known to damp out the nutational oscillation quickly. So the physicist is prepared for the phenomenon of gravity being overshadowed by rotational kinetic energy. Slightly more experienced physicists know about the friction torque which acts to lift up a normal top: indeed it can be observed that a top started at a tilt will lift itself up and align the angular momentum vector with the vertical.
What most (even experienced) physicists are not ready for in the case of a spherical top is the fact that: (i) frictional torques dominate the behaviour of the motion; (ii) the
theta=0
orientation is quite unstable and spinning about the rotor axis gives way to precessional motion for any such top, almost irrespective of the mass arrangement provided the initial spin rate is sufficiently high; (iii) energy dissipation is rather large and leads to tippy-top orientations with
theta>Pi/2
, and for some range of moment of inertia regimes
I1=I2
versus
I3
to a definite push towards
theta=Pi
. It is the latter behaviour which leads to the phenomenon of the tippy-top standing up on its stem.
To model the entire motion of the tippy-top from beginning to end is complicated, but has recently been achieved by Christian Friedl and together with Andre Wobst from the University of Augsburg in Germany turned into virtual reality movies [
www.physik.uni-ausburg.de/~wobsta/tippetop
]. In this worksheet we will restrict the discussion to that of a spherical top with center of gravity on the rotor axis below the geometrical center. The sphere is described by two principal moments
I1=I2
and
I3
. Following the work of Friedl, which has been in part inspired by the interesting paper of Leutwyler [European Journal of Physics
15
, 59 (1994); which most clearly discusses the stability regimes for the nutation angle theta] we discuss not only the numerical solution of Euler's equations for such a sphere, but also illustrate a conservation law.
The physicist is baffled by the tippy-top, because the orientation of the top at the beginning is clearly favoured by gravity. Without spinning the gravitational torque lifts the top into the position with the stem up. Why then is the
theta=0
orientation unstable for high spin rates? Why in fact, does the top stand up on its stem, obviously going to the most unfavourable orientation from gravity's perspective? Clearly rotational energy is given up during this turning upside-down process. The only torque to remove rotational kinetic energy is the frictional torque which acts about the vertical. Given that friction is important to qualitatively determine the motion traditional physicists might become nervous, because most textbook examples deal with energy-cosnserving systems, or systems where energy is removed slowly (such as in the nutational motion of the normal top or gyroscope). It turns out that the gravitational potential energy in the tippy-top is dwarfed by the rotational kinetic energy, and can practically be left out of the discussion (for high initial spin rates). It is small, because the displacement of the center of gravity from the center of the sphere (labeled by the variable
a
) is small, i.e., the gravitational torque is small (one really is interested in the torque due to the normal force in response to gravity, because the lever arm originates in the centre of mass-CM).
Why is there hope for some analytical results even though energy is not conserved, and obviously the vertical component angular momentum is not conserved. The latter point makes the physicist even more nervous, because conservation of the vertical component of angular momentum in the laboratory frame provides the main argument for understanding precession, and in particular for understanding why the precession picks up speed when the gyro slows down. The tippy-top spins much more slowly in its upside-down position than in the original starting orientation, i.e., a large amount of kinetic energy has been dissipated. The
z-
component (lab frame) of angular momentum is substantially reduced, but it still points in the same direction. This means that from the body frame point of view the spin angular velocity about the rotor axis has changed sign! Wow, why would it do that?
Nevertheless, for the simpler forms of friction forces there remains a conserved quantity. The dot product of the angular momentum vector
L
and the position vector
r
which describes the location of the point of contact with the surface (table) as measured from the center of mass (gravity) (CM) of the top (a sphere of radius
R
) can be shown to be conserved in time when the friction is of sliding type. This is done, e.g., in an AJP paper by B.G.Nickel and C.G.Gray [Am. J. Phys
68
, 821 (2000), where a very comprehensive review of the history of the subject can be found] although overall the paper is not easy to understand, because it presents many results based on energy conservation (while stressing at the beginning that energy dissipation is crucial). Leutwyler has probably been the first to intuitively explain how the frictional torques work: when the tippy-top goes into spin+precessional motion the CM executes motion in a circle about the point of contact, i.e., there is constantly friction at play. Cohen argues that the moment arm for the frictional torque in the spin motion about the rotor axis goes like
R*sin(theta)
, i.e., becomes large when the top leaves the vertical orientation. This is one reason for the motion favouring the precessional motion (the stem visibly spinning about the vertical, while also nutating). While this is a nice argument (the moment arm remains small for the precessional rotation), one should watch the time evolution of the angular velocities, and one will notice that a dramatic change in behaviour occurs at
theta=0
(most simulations start at a small non-zero value, seem to tend towards
theta=0
, where a big 'bounce' occurs exchanging the rotational kinetic energies in the spin and precessional motions. So perhaps more importantly Leutwyler stresses that the motion becomes stable when the frictional torque is minimized. The frictional torque acts such as to minimize the velocity of the CM of the top in the
(x,y)
plane. This can occur at
theta=0
or at
theta=Pi
, but also at other values of
theta
when the moments of inertia are chosen differently. The numerical simulations of Cohen (and later Friedl) have found examples for this dependence on the relationship of the moment of inertia values
I1
and
I3
.
Our goal is to present the equations of motion for the top without translational motion of the CM. Nevertheless, as explained in the previous paragraph, the CM will be moving about the point of contact in a circular fashion (except when
theta=0
or
theta=Pi
), and frictional torques govern the motion. We will follow the Newton-Euler equations of motion as outlined by Cohen rather than the Lagrange-Hamilton formalism employed by Friedl (which is convenient to observe the conservation law, and to model more complicated friction torques based on a dissipation function). We cannot derive the equations here, but refer to the paper and to the lecture notes (jpg-files). Nevertheless, we outline some key ideas.
The laboratory frame is defined by
(x,y,z)
. The table is represented by the
(x,y)
plane in which the circular motion of the CM about the contact point
T
occurs. The body frame is denoted by
(1,2,3)
with
3
being the rotor axis. The orientation of the top in the laboratory is described by: the nutation angle
theta
between the
3-
and the
z-
axis; a unit vector
e
_n
formed by the cross product of
e
_z
and
e
_3
(normalized to unit length) - this vector forms the precession angle
phi
with the
e
_x
unit vector; a unit vector
e
_np
obtained from the cross product of
e
_3
and
e
_n
. The coordinate system
(n,np,3)
defines the orientation of the top, the top's spinning about the rotor axis is described by the
(1,2)
axes rotating with respect to
(n,np)
by angle
psi
. Cohen lists the relationships between these unit vectors in equations (2)-(9), this is nothing but geometry.
The angular velocity vector
w
as measured in the laboratory frame has components in
(n,z,3)
coordinates
(theta-dot, phi-dot, psi-dot)
- where
dot
refers to time derivative. This is simply in accord with the definition of the angles (
theta
turns about
n
,
phi
about
z
, and
psi
about
3
; see Fig. 4 in Cohen). This needs to be expressed in the orthogonal
(n,np,3)
coordinate system, where the components become
(theta-dot, phi-dot*sin(theta), psi-dot+phi-dot*cos(theta))
. The
(n,np,3)
coordinate system itself has an angular velocity vector in the lab frame which is almost identical to
w
for the top, the only difference being the absense of the
psi-dot
in the
3-
component. This is the same choice of coordinates as for the discussion of the Euler equations for the gyroscope.
In eq. (12) Cohen discusses the simplest-possible frictional torque that can explain the tippy-top. The argument is that the friction force for rotation of the CM about T (without translation on the table surface) the friction force points along
-
e
_n
. A rotation of the CM riding on the
3-
axis has a tangential velocity vector aligned with
e
_n
, given that it is perpendicular to
e
_z
and
e
_3
. A kinetic coefficient of friction (
f=0.3
or less) is assumed and the magnitude of the friction force becomes
f*m*g
, where
m
is the mass of the top. This simplistic friction model does not damp the nutation (Cohen generalizes it in eq. (16)). The frictional torque is calculated by taking the cross product with
r
= (a*e_3 - R*e_z)
, which results in components along
e
_np
and
e
_3
(but not
e
_n
). We generalize eq. (12) to include damping of the nutation, and also to account for the sign-change when the Cartesian velocity components reverse direction. In a separate section the complete cross product according to eq. (16) is calculated (resulting in messy expressions). The answers can be copy-pasted and used as a replacement for the frictional torques.
The rest is the usual Euler equation treatment: A frame was chosen in which the moments of inertia remain constant (the orientation frame for the top described above). The Euler equations are straightforward, the rate of change of the angular momentum vector in the laboratory frame is related to the rate of change in the body frame (where we acquire the
omega-cross-L
term which leads to the nonlinearities of the Euler equation). The friction torque has been translated from the lab frame to the body frame, and the gravitational torque will turn out to be irrelevant (but could be added easily). The equations are then differentiated to obtain second-order equations for the angles.
MOST USERS WILL SKIP THE DERIVATION IN THE INDENTED SECTION BELOW:
The frictional torque about the CM in (n,n',3) coordinates according to eq.(16) in R.Cohen
Calculate the frictional torque by evaluating the cross product.
Warning, the protected names norm and trace have been redefined and unprotected
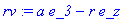
| > |
sth:=sin(theta(t)): cth:=cos(theta(t)):
|
| > |
sph:=sin(phi(t)): cph:=cos(phi(t)):
|
| > |
e_3:=vector([sth*sph,-sth*cph,cth]);
|
![e_3 := vector([sin(theta(t))*sin(phi(t)), -sin(theta(t))*cos(phi(t)), cos(theta(t))])](images/TippyTop2.gif)
![e_z := vector([0, 0, 1])](images/TippyTop3.gif)
![vector([a*sin(theta(t))*sin(phi(t)), -a*sin(theta(t))*cos(phi(t)), a*cos(theta(t))-r])](images/TippyTop4.gif)
Now enter the friction force in Cartesian coordinates: first do
[-vx,-vy,0]
and multiply on the remaining factors
f*m*g/vR
at the end.
| > |
F_f:=-vector([(r*psidot(t)+a*phidot(t))*sth*cph+thetadot(t)*sph*(a*cth-r),(r*psidot(t)+a*phidot(t))*sth*sph-thetadot(t)*cph*(a*cth-r),0]);
|
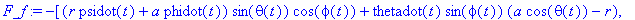
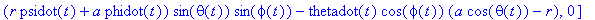
In cartesian coordinates the torque becomes (up to factors -f*m*g/vR):
| > |
N_fCC:=crossprod(evalm(rv),F_f);
|

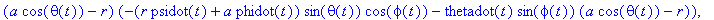
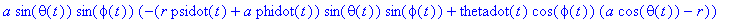
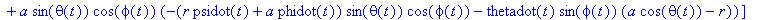
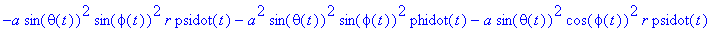
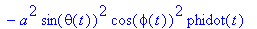
| > |
simplify(%,{cph^2+sph^2=1,cth^2+sth^2=1});
|

Now we want the components of the torque in the (n,np,3) reference frame. For this purpose we define the transformation:
| > |
e_x:=cph*e_n-cth*sph*e_np+sth*sph*e_3;
|
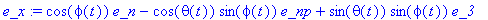
| > |
e_y:=sph*e_n+cth*cph*e_np-sth*cph*e_3;
|
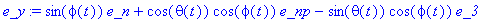
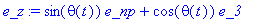
| > |
N_f:=N_fCC[1]*e_x+N_fCC[2]*e_y+N_fCC[3]*e_z;
|
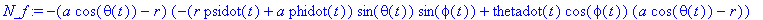
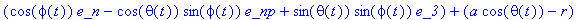
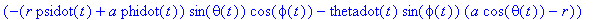
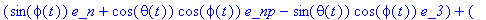
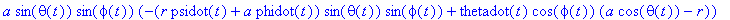
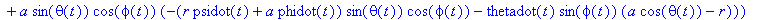
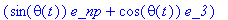
The magnitude of the velocity of the CM about the contact point T projected onto the x-y plane is given as
| > |
vR:=sqrt((a*phidot(t)+r*psidot(t))^2*sth^2+thetadot(t)^2*(r-a*cth)^2);
|
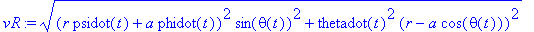
| > |
Nn:=factor(simplify(expand(coeff(N_f,e_n)),{cph^2+sph^2=1,cth^2+sth^2=1}))*f*m*g/vR;
|
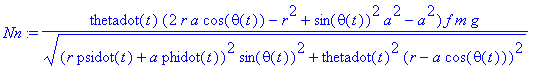
| > |
Nnp:=factor(simplify(expand(coeff(N_f,e_np)),{cph^2+sph^2=1,cth^2+sth^2=1}))*f*m*g/vR;
|
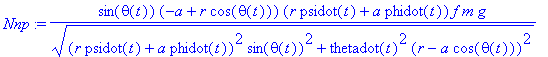
| > |
N3:=factor(simplify(expand(coeff(N_f,e_3)),{cph^2+sph^2=1,cth^2+sth^2=1}))*f*m*g/vR;
|
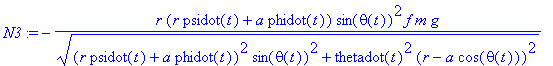
Rather than using those messy expressions, we expand a little on the simple friction torque modeling introduced in eq. (12). In eq.(12) it was simply assumed that the kinetic sliding friction force is along the negative
e
_n
axis. This is valid when the original spin about the 3-axis is positive, and ignores the velocity component of the CM associated with nutations. If one inputs the torque (12) as is, the tippy-top stands up, reaches
theta=Pi
for many conditions (almost independently of
I1
and
I3
), and then bounces and the friction torque starts dumping energy into the rotational motion. It also gives energy gain when the top is started with a negative value of
psidot(0)
. To obtain a more realistic model we added the torque component about the
e
_n'
axis, and introduced a sign dependence. From the discussion of the velocity, eq. (14) [it is given in the above section], it is obvious that the sign dependence shoulf be on
thetadot(t)
, and on the combination
(r*psidot(t)+a*phidot(t))
. When we use the discontinuous (unevaluated)
sign(x)
function in Maple, the differential equations solver is knocked out. Thus, we use a softened sign function made up from the
arctan
function with scaled argument. The dependence on the scale parameter should be tested.
| > |
#plot(2/Pi*arctan(100*x),x=-1..1);
|
| > |
sth:=sin(theta(t)): cth:=cos(theta(t)):
|
We list the magnitude of the velocity of the CM projected onto the table surface. It shows how the components
v_x
and
v_y
change sign when the variables
thetadot
or
a*phidot+r*psidot
change sign (go through zero).
| > |
vR:=sqrt((a*phidot(t)+r*psidot(t))^2*sth^2+thetadot(t)^2*(r-a*cth)^2);
|
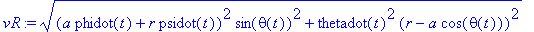
| > |
# in theta-eq: gravitational (normal force) torque: -m*g*a*sth
|
We introduce the simple frictional torques in the
n'
and
3
-directions. They are based on sliding kinetic friction proportional to the magnitude of the normal force and opposing the velocity, which at this point is not used with known sign.
| > |
Sign:=x->2/Pi*arctan(1000*x);
|
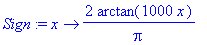
| > |
Nn:=-m*g*a*sth; # to try eq. (12) & with gravitational torque
|
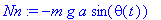
| > |
#Nn:=-m*g*a*sth-f*m*g*abs(r*cth-a)*Sign(thetadot(t)); # This friction about n-axis is too large
|
| > |
Nnp:=f*m*g*(r*cth-a)*Sign((r*psidot(t)+a*phidot(t)));
|

| > |
N3:=-f*m*g*r*sth*Sign((r*psidot(t)+a*phidot(t)));
|
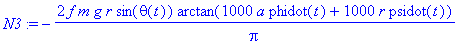
Manually calculated torques from eq (16): unfortunately
dsolve[numeric]
can't integrate the equations with them beyond a point where
theta(t)
is very small. The answer would be to use the torques Nnp and N3, and keep only the gravitational torque (normal force at T).
| > |
#Nn:=-m*g*a*sth-f*m*g*(r-a*cth)^2*thetadot(t)/vR; # this frictional torque gives trouble.
|
| > |
#Nnp:=-f*m*g*(a-r*cth)*(r*psidot(t)+a*phidot(t))*sth/vR;
|
| > |
#N3:=-f*m*g*r*sth^2*(r*psidot(t)+a*phidot(t))/vR;
|
| > |
DE1:=diff(theta(t),t)=thetadot(t);
|
| > |
DE2:=diff(phi(t),t)=phidot(t);
|
| > |
DE3:=diff(psi(t),t)=psidot(t);
|
| > |
DE4:=diff(thetadot(t),t)=phidot(t)^2*sth*cth*(1-I3/I1)-(I3*phidot(t)*psidot(t)*sth-Nn)/I1;
|
| > |
DE5:=diff(phidot(t),t)=((I3-2*I1)*phidot(t)*thetadot(t)*cth+I3*psidot(t)*thetadot(t)+Nnp)/(I1*(sth));
|
| > |
DE6:=diff(psidot(t),t)=phidot(t)*thetadot(t)*sth-cth*diff(phidot(t),t)+N3/I3;
|
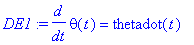
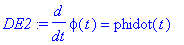
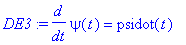
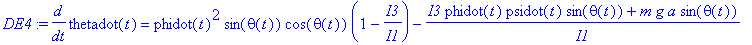
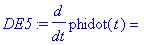
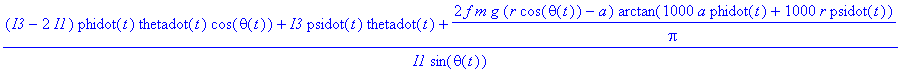

Now set the parameters I1=9E-7 stable theta around 2.2, tippy doesn't get up. I1=8E-7: gets all the way.
| > |
I1:=7.5E-7; I3:=7.0E-7;
|
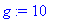
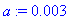
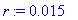
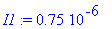
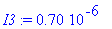
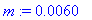
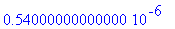
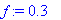
| > |
IC:=theta(0)=0.1,phi(0)=0,psi(0)=0,thetadot(0)=0,phidot(0)=0,psidot(0)=150;
|
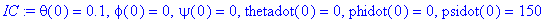
| > |
sol:=dsolve({seq(DE||i,i=1..6),IC},numeric,method=rosenbrock,output=listprocedure):
|
| > |
Theta:=eval(theta(t),sol): Thetadot:=eval(thetadot(t),sol): Phi:=eval(phi(t),sol): Phidot:=eval(phidot(t),sol): Psi:=eval(psi(t),sol): Psidot:=eval(psidot(t),sol):
|
In the following line we test the numerical integration: if it fails to go beyond some time limit due to inability to cope with adaptive error control requirements we simply choose manually a time integration limit
t_f
that allows us to display results.
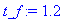
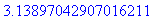
| > |
plot([Theta(t)],t=0..t_f,numpoints=500,color=[red,blue]);
|
![[Maple Plot]](images/TippyTop51.gif)
| > |
plot([Psidot(t),Phidot(t),Thetadot(t)],t=0..t_f,numpoints=500,color=[red,blue,green],view=[0..t_f,-150..250]);
|
![[Maple Plot]](images/TippyTop52.gif)
These graphs show clearly that the exchange of rotational energy between the
psidot
and
phidot*sin(theta)
degrees of freedom happens when
theta
becomes small, and the reversal occurs when the top 'bounces' at
theta=0
. This makes one nervous naturally, whether the numerics are all in order. Strange behaviour can happen also for
theta=Pi
.
We display the rotational kinetic energy to demonstrate the energy dissipation, and also the total energy in order to justify the omission of the gravitational torque (actually the torque due to the normal force that acts at the contact point T).
| > |
Trot:=t->(I3*(Psidot(t)+Phidot(t)*cos(Theta(t)))^2+I1*((sin(Theta(t))*Phidot(t))^2+Thetadot(t)^2))/2;
|
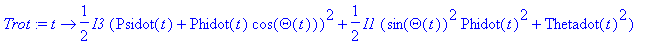
| > |
plot([Trot(t),Trot(t)-m*g*a*cos(Theta(t))],t=0..t_f,title="Rotational Energy (red) and Total Energy (blue)",view=[0..t_f,0..1.1*Trot(0)],color=[red,blue]);
|
![[Maple Plot]](images/TippyTop54.gif)
It can be seen that a small amount of energy goes also into lifting up the tippy-top in the gravitational field, but for all practical purposes it can be ignored.
Below we demonstrate that the dot product of the angular momentum vector with the psoition vector of the contact point as measured from the CM of the tippy-top is conserved. This conservation would be violated slightly if we included a friction torque about the z-axis which described a depression of the sphere into the table surface, i.e., the friction torque would not apply at the point of contact, but a contact surface of finite size would be involved. This type of friction results in a slowdown of the top while in the vertical position (
theta=0, Pi
).
| > |
Ldotr:=t->I3*(Psidot(t)+cos(Theta(t))*Phidot(t))*(a-r*cos(Theta(t)))-I1*r*sin(Theta(t))^2*Phidot(t);
|
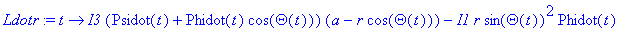
| > |
seq(Ldotr(t_f/10*i)/I1,i=0..10);
|
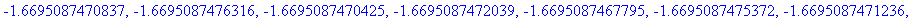
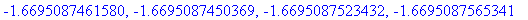
The result is negative, because the angle between
L
and
r
is above
Pi/2
. If the numbers vary, the plot command below can be used:
| > |
#plot(Ldotr(t)/I1,t=0..t_f,title="(L dot r)/I1");
|
The conservation of the dot product of
L
and
r
allows one to calculate the required amount of kinetic energy which has to be dissipated by the frictional torque in order to put the tippy top upside down. Assuming that we move from the
theta=0
to the
theta=Pi
configuration we find that the dot product is given by
I3*psidot(0)*(r-a)*(-1) = I3*psidot(t_f)*(r+a)*(-1)
. Therefore the kinetic energy changes by a factor of
((R-a)/(R+a))^2
. This is indeed observed in the energy graph above. Of course, for a more realistic tippy-top the transfer of energy to the translational degrees of freedom plays also some role. Nevertheless, the knowledge of this quantity can help in the design of more successful tippy-tops, namely tops that wind up with a more substantial fraction of their original rotational kinetic energy in the upside-down configuration. Now it seems that sending
a
to zero would give the best results, in that the least amount of kinetic energy would be needed to put the tippy-top upside down (and the gravitational potential to overcome would also be minimized!). It turns out that there is a qualitative change in the solution when
a/r
falls below 0.1, which makes it unlikely for the tippy-top to work (even though the equations display the instability). In this regime the solution demonstrates that
psidot
and
phidot
can exchange rotational energy without energy dissipation, but that energy dissipation is needed to carry out the
theta
-motion, which happens rapidly at a later time in this case. Also note that in this regime the results are very sensitive to the relationship between the moments of inertia
I1
and
I3
, and that
a
and
I1
are not independent of each other when the tippy-top is made of homogeneous material using cut-outs as a method to move
a
along the rotor axis.
| > |
T_fin_over_T0:=((r-a)/(r+a))^2;
|
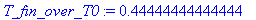
Exercise 1:
Reduce the initial spin rate by, e.g., a factor of three to 50 rad/sec. What do you observe? How would you explain the difference in behaviour? If you have access to a tippy-top perform experiments to support your findings.
Exercise 2:
Model a smoother table surface, i.e., reduce the kinetic friction constant
f
by a factor of 2 (to 0.15), and then by another factor of 2 (to 0.075). What do you observe? What does this imply about the importance of the frictional torque?
Exercise 3:
Remove the torque due to the normal force (the reaction force to gravity), i.e., keep only the frictional torque in the Euler equations. Compare the answers for different initial conditions (initial spin rates) with the full calculations and explain your observations.
Exercise 4:
Change the initial condition such that the tippy-top starts with pure precession in the
theta=Pi/2
orientation. Describe your results for different values of the precession rate (e.g., 50, 100, 150 rad/s). If you have access to a tippy-top perform experiments to support your findings.
Exercise 5:
Change the design parameters of the tippy-top (start with moments of inertia, then proceed with the
((r-a)/(r+a))
ratio), and observe the changes in the numerical solution. For example: an increase of
I1
by 20% (while the other parameters remain the same) can have the result that the tippy-top will stabilize at a
theta
-value substantially below
Pi
.
Exercise 6:
The present treatment used a normal force in the frictional torque calculation which ignored the fact that the CM is accelerated up and down when
theta
changes. The height of the CM is given as
z_CM(t) = R-a*cos(theta(t))
. The second derivative is given as
diff(z_CM(t),t$2) = a*(thetadot(t)^2*cos(theta(t))+diff(thetadot(t),t)*sin(theta(t)))
, and the normal force equals
m*g+m*diff(z_CM(t),t$2)
. Include this correction and find out to what extent it changes the results. What is your expectation before you start the work?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
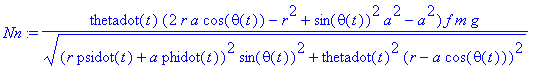
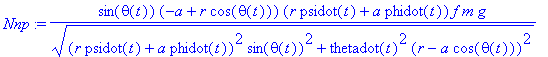
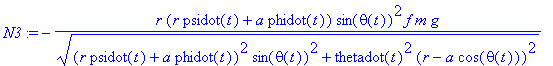
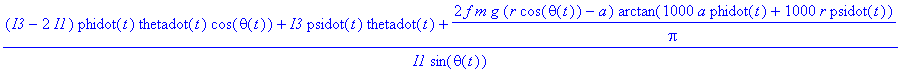
![[Maple Plot]](images/TippyTop51.gif)
![[Maple Plot]](images/TippyTop52.gif)
![[Maple Plot]](images/TippyTop54.gif)