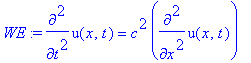WaveEqn.html

WaveEqn.html WaveEqn.mws

Wave equation

Classical mechanics texts discuss the wave equation as an example of continuous many-particle systems where the particles are connected by springs. One derivation can be found in Cassiday and Fowles (6th ed., chapter 11.5/6) the summary of which is given in the page WaveEqn.jpg . An example of a finite system of masses coupled by springs to simulate vibrations is given in Glass.mws .

The wave equation contains a constant, namely the square of the propagation speed for the waves which we call c . In classical mechanics (transverse vibrations of a continuous string) the square of the speed equals the string tension divided by the linear mass density. The wave equation plays an important role in electromagnetism, where it is derived from Maxwell's equation for the electromagnetic fields.

Our interest is in applying the Fourier series to solve the wave equation in one dimension for a plucked string. We have used this technique in the analysis of the one-dimensional heat equation ( HeatEqn.mws ), and explored it further in FourierSeries.mws . u(x,t) denotes the vertical (transverse) displacement of the string as a function of location and time. The assumption is that no longitudinal motion occurs, which can be achieved in the small-amplitude limit.

The equation (in mechanics) inherits the two time derivatives from Newton's equation. The two spatial derivatives arise as a consequence of the harmonic force experienced by a mass point from its two neighbours: the difference of relative displacements can be expressed as a difference of first derivatives, and thus as a second derivative with respect to location.

> restart;

> WE:=diff(u(x,t),t$2) = c^2*diff(u(x,t),x$2);

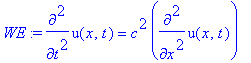We choose a unit system in which 0 < x < 1 , and c=1 .

> sol:=pdsolve(WE);

Maple's pdsolve engine realizes that the solutions to the wave equation can be expressed as a sum of a left-travelling and a right-travelling wave solution. While this is interesting in its own right (waves on the string can cross, standing wave solutions are possible) this is not necessarily directly useable to find the answer.

> c:=1;

> pdsolve(WE,HINT=f(x)*g(t));

$`&where`(u(x,t) = f(x)*g(t),[{diff(f(x),`$`(x,2)) = _c[1]*f(x), diff(g(t),`$`(t,2)) = _c[1]*g(t)}])$

If we ask Maple for a solution in product form we are reminded of how separation of variables connects the spatial and temporal parts in the solution. The structure of the ODEs is identical, but we usually have a boundary-value problem in space, and an initial-value problem in time. _c1 is the separation constant.

Let us fix the string at the endpoints.

> ODE_x:=diff(f(x),x$2)=c1*f(x);

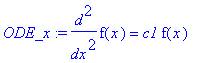This is a differential-equation eigenvalue problem which defines a Fourier basis. The condition that the string be fixed at x=0 is used to select sine-solutions only, i.e., it removes one integration constant. The other boundary condition selects the eigenvalue c1 . The amplitude of the sine-wave solutions is arbitrary, because the problem is homogeneous (an eigenvalue problem always is). The eigenvalues are negative (for sine/cosine type solutions) and correspond to the negative of the square of the wavenumber k in the sin(k*x) solutions. Let us find them.

> sol_x:=dsolve({ODE_x,f(0)=0});

This reminds us of the fact that the trig solutions can be expressed as complex exponentials. Those are less intuitive.

> assume(c1<0);

> sol_x:=dsolve({ODE_x,f(0)=0});

Now demand that the solution vanish at the right boundary, i.e., at x=1 :

> solve(sin(k*1)=0,k);

This solution is uninteresting, as it yields the trivial solution f(x)=0 . How do we make Maple give us the interesting solutions?

> _EnvAllSolutions := true:

> solve(sin(k*1)=0,k);

OK, this we know from high school. Integer multiples of Pi will work for k .

> k_n:=n->n*Pi;

> fB:=n->sin(k_n(n)*x);

The separation constants:

> c_n:=n->-k_n(n)^2;

Are these basis functions normalized?

> IP:=(f1,f2)->int(expand(f1*f2),x=0..1);

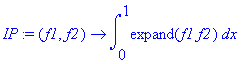> IP(fB(1),fB(1));

> IP(fB(2),fB(2));

> IP(fB(5),fB(5));

This is no proof, but evidence that we should redefine our basis functions:

> fBn:=n->sqrt(2)*sin(k_n(n)*x);

> IP(fBn(1),fBn(3));

> IP(fBn(3),fBn(3));

Orthonormality of the basis seems to be satisfied; check this out by trying different values for n1 , n2 .

The next question is: how do these basis states evolve in time? The separation constant specifies their time behavior:

> ODE_t:=diff(g(t),t$2)=c1*g(t);

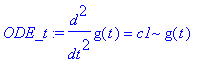> dsolve(ODE_t);

Two initial conditions are required to specify the temporal behaviour of each mode (usually the initial displacement, and the intial velocity).

For the case of a plucked string we can argue that we have a known initial configuration of the string, and zero time derivative for this configuration at the beginning. This would imply that we are interested in cosine-type temporal solutions only. Another intial condition would be to be in the equilibrium configuration with an intial velocity profile brought on by, e.g., a hammer hitting the string at some time. This would call for sine-type solutions only. The general case would be covered by having a superposition of both types, as expressed above.

Each mode has a different value of c1 , and therefore oscillates with a different frequency.

The actual superposition of modes required is obtained by projecting the initial configuration onto the Fourier basis. Suppose we displace the string at time zero such that it has a height a in the middle (for x=1/2 ), and is linear in-between.

> a:=1/10;

> f0:=piecewise(x<1/2,2*a*x,x>1/2,2*(a-a*x));

> plot(f0,x=0..1);

A Fourier representation for a finite basis size:

> Nb:=9;

> b:=[seq(IP(f0,fBn(j)),j=1..Nb)];

> f0_ap:=add(b[j]*fBn(j),j=1..Nb);

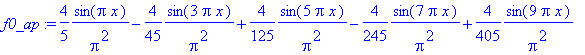> plot([f0,f0_ap],x=0..1,color=[red,blue]);

The approximation of the intial configuration is OK. Expand the basis size and observe how it improves!

Now we assemble the full solution to the wave equation:

> sol_WE:=add(b[j]*fBn(j)*cos(sqrt(-c_n(j))*t),j=1..Nb);

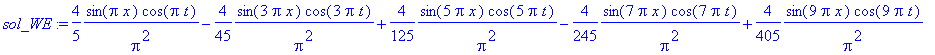> plot3d(sol_WE,x=0..1,t=0..5,axes=boxed);

A better presentation is given by an animation in 2d:

> with(plots):

> animate(sol_WE,x=0..1,t=0..5,frames=50);

Exercise 1:

Change the location at which the string is plucked away from the midpoint. What observation do you make about the Fourier coefficients as compared to the present case?

Exercise 2:

Change the intial condition to represent a case where the string is in equilibrium, but is hit with a hammer.

Exercise 3:

Graph the time evolution of the first three modes. Find the relationship between the frequencies for these modes.

>