Atomic Lifetimes

A calculation of the lifetimes of excited atomic hydrogen levels associated with the spontaneous decay. The basics are explained in Liboff, some details are provided in Bethe-Salpeter.

First we need normalized hydrogen wavefunctions with separate radial and angular parts.

>

restart;

>	with(plots):

Warning, the name changecoords has been redefined

We define the radial wavefunctions for hydrogen and the corresponding radial integrals:

>	F:=(n,l,r)->simplify(add((-1)^i*((n+l)!)^2*r^i/(i!*(n-l-1-i)!*(2*l+1+i)!),i=0..n-l-1));

>

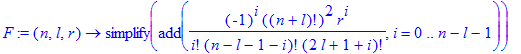
F(1,0,r);

>

F(2,0,r);

>

F(2,1,r);

>	A:=(n,l)->sqrt((n-l-1)!/(2*n*((n+l)!)^3));

>

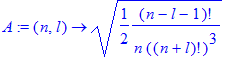
Z:='Z';

>	#assume(Z>0);

>	R:=proc(n,l,r) local k,rho; global Z;

>	k:=Z/n; rho:=2*k*r;

>	A(n,l)*rho^l*exp(-rho/2)*F(n,l,rho)*(2*k)^(3/2); end:

>

R(1,0,r);

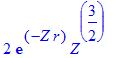
>	int(%^2*r^2,r=0..infinity) assuming Z>0;

>

R(2,0,r);

>	int(%^2*r^2,r=0..infinity) assuming Z>0;

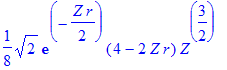
>	simplify(R(2,1,r));

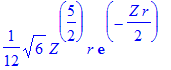
>	int(%^2*r^2,r=0..infinity) assuming Z>0;

>	plot([subs(Z=1,r*R(4,0,r)),subs(Z=1,r*R(4,1,r)),subs(Z=1,r*R(4,2,r)),subs(Z=1,r*R(4,3,r))],r=0..60);

These radial functions are normalized. Are they orthogonal?

>	int(expand(R(2,0,r)*R(1,0,r)*r^2),r=0..infinity) assuming Z>0;

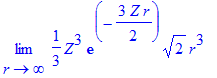
Maple should not have trouble with this! For some reason maple9.03 or 9.5 doesn't figure this one out.

The angular parts of any central-force problem are spherical harmonics.

>	with(orthopoly);

>	Plm:=proc(theta,l::nonnegint,m::integer) local x,y,f;

>	x:=cos(theta);

>	if m>0 then f:=subs(y=x,diff(P(l,y),y$m));

>	else f:=subs(y=x,P(l,y)); fi;

>	(-1)^m*sin(theta)^m*f; end:

>	Plm(theta,3,2);

For the spherical harmonics we don't need the Plm's with negative argument.

>	Y:=proc(theta,phi,l::nonnegint,m::integer) local m1;

>	m1:=abs(m); if m1>l then RETURN("|m} has to be <= l for Y_lm"); fi;

>	exp(I*m*phi)*Plm(theta,l,m1)*(-1)^m*sqrt((2*l+1)*(l-m1)!/(4*Pi*(l+m1)!)); end:

>	Y(theta,phi,3,0);

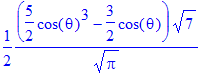
>	Y(theta,phi,3,1);

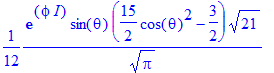
>	No:=(l,m)->int(int(evalc(Y(theta,phi,l,m)*conjugate(Y(theta,phi,l,m))),phi=0..2*Pi)*sin(theta),theta=0..Pi);

>

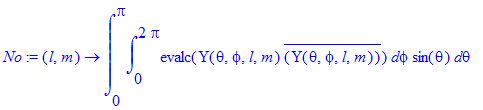
No(1,0);

>

No(1,1);

Suppose I need to calculate the electrostatic potential for a wavefunction in a superposition of hydrogenic orbitals.

What is the angular dependence of the product terms?

>	IP:=(f,g)->int(int(evalc(g*conjugate(f)),phi=0..2*Pi)*sin(theta),theta=0..Pi);

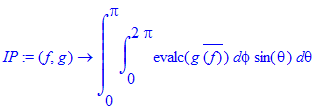
>	IP(Y(theta,phi,1,0),Y(theta,phi,3,0));

The required matrix element involves as the operator the position vector [x, y, z]  expressed as  r*[sin(theta)*cos(phi), sin(theta)*sin(phi), cos(theta)]

The radial part of the matrix element is defined first. We need to set the charge:

>

Z:=1;

>	RME:=(n,l,np,lp)->int(r^3*R(n,l,r)*R(np,lp,r),r=0..infinity);

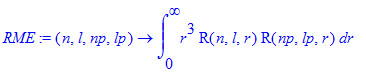
>	RME(2,1,1,0);

Now the part where the polar and azimuthal angles theta and phi are integrated:

>	AME:=(l,m,lp,mp)->abs(IP(Y(theta,phi,l,m),sin(theta)*cos(phi)*Y(theta,phi,lp,mp)))^2+abs(IP(Y(theta,phi,l,m),sin(theta)*sin(phi)*Y(theta,phi,lp,mp)))^2+abs(IP(Y(theta,phi,l,m),cos(theta)*Y(theta,phi,lp,mp)))^2;

>	AME(1,0,0,0);

The phase-space factor omega^3  is defined now, where hbar*omega  is the photon energy calculated from the difference of electronic energy levels. We choose atomic units in which hbar=m=e=1 :

>	ED:=(n,np)->-Z^2/2*(1/n^2-1/np^2);

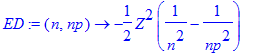
>	c:=137.04: alpha:=1/c:

>	Acof:=(n,l,m,np,lp,mp)->evalf(RME(n,l,np,lp)^2*AME(l,m,lp,mp)*ED(n,np)^3*4/3*alpha/c^2,4);

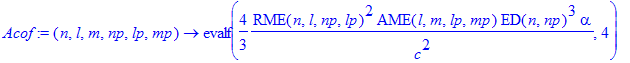
>	Acof(2,1,0,1,0,0);

This is the A coefficient in atomic units. To obtain the lifetime, we take the inverse, and convert to nanoseconds. The atomic time unit is approximately 2.4E-17 s?

In nanoseconds:

>	atu:=2.418884E-17; # the atomic time unit to 7 digits (it is known more accurately)

>	evalf(1/Acof(2,1,0,1,0,0)*atu*1E9,3);

The special case of maximal angular momentum states which can only decay to the nearest neighbour:

>	C1:=n->evalf(1/Acof(n,n-1,n-1,n-1,n-2,n-2)*atu*1E9,4);

>

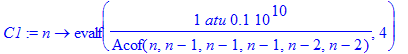
C1(2);

>	seq(C1(n),n=2..20);

These numbers look right when compared to an analytic evaluation of the integrals. In particular, they can be compared with the closed-form expression (31) in M Seidl and P O Lipas: Eur. J. Phys. 17, 25 (1996) for the lifetimes in nanoseconds:

>	C1a:=n->evalf(0.0622*3*n^4*(n-1)^2/(2*n-1)*(1+1/4/n/(n-1))^(2*n),4);

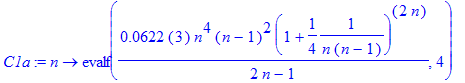
>	seq(C1a(n),n=2..20);

For other initial states (non-maximal angular momentum), the situation is more complicated due to the presence of various decay channels. We begin by providing explicit expressions that sum over the allowed m -sublevels. The selection rules are: +/- 1  in l  (L), and 0, +/-1  in m . For the initial state we pick n,l,m . We need to know how Acof  responds for non-allowed cases.

>	Acof(2,1,0,2,2,0);

Error, (in A) numeric exception: division by zero

Thus, we need to protect the procedure from illegal calls.

>	AcofSp:=(n,l,m,np)->if l+1 < np then add(Acof(n,l,m,np,l+1,mp),mp=max(m-1,-l-1)..min(m+1,l+1)) else 0 fi;

>	AcofSp(2,1,0,1);

>	AcofSp(4,1,1,3);

>	AcofSp(4,1,1,2);

Why would the last one be forbidden? 4p1->2d final state does not exist.

Now look at lowering  l  (L) by one unit.

>	AcofSm:=(n,l,m,np)->if l-1 < np and l-1>=0 then add(Acof(n,l,m,np,l-1,mp),mp=max(m-1,-l+1)..min(m+1,l-1)) else 0 fi;

>	AcofSm(4,2,1,2),AcofSm(4,2,1,3);

This shows the phase-space factor effect. The Einstein coefficient provides a decay rate: the decay from n=4  is faster to n=2  than it is to n=3 .

Now let us demonstrate that the decay rate for the case when l  decreases beats the one for increasing l .

>	AcofSm(4,1,0,3),AcofSp(4,1,0,3);

There is almost an order-of-magnitude difference. The answer is independent of the initial magnetic quantum number (apart from inaccuracies).

>	AcofSm(4,1,-1,3),AcofSp(4,1,-1,3);

Exercise 1:

Calculate the transition rates to all possible final states for |3s>, |3p>, |3d>, and for |4s>, |4p>, |4d>, |4f> and compare them to a table (e.g., Radzig+Smirnov). Then calculate the total transition rates and lifetimes for these states.

>