The H-atom in parabolic coordinates

Our aim here is to demonstrate what some hydrogen atom eigenfunctions look like when expressed in parabolic coordinates. A few points are demonstrated by this:

1) for a pure Coulomb potential the separation in spherical polar coordinates is not the only way to proceed; eigenfunctions can be found which are not eigenfunctions of the angular momentum operator L^2 ;

2) for a pure Coulomb potential some additional symmetries are present beyond spherical symmetry; these symmetries (conservation law) are responsible for the n - l  degeneracy of the spectrum; they make the separation possible in another set of coordinates; the conservation law behind this symmetry is the conservation of the Laplace-Runge-Lenz vector (as an operator in QM);

3) the usual angular momentum eigenstates can be expressed as linear combinations of the eigenstates in parabolic coordinates;

4) the eigenstates in parabolic coordinates are useful when additional interactions are turned on, such as a constant electric field along the (chosen) z -axis.

To save time on computational steps we do not re-derive the energy spectrum (although it can be done!). Our purpose is to demonstrate what the probability (charge) density looks like for the new eigenstates.

The new eigenstates are classified by

m  - quantum number for the L_z  eigenvalues (as before);

n1  - quantum number for the first 'radial' function in the xi-coordinate, xi=r+z ;

n2  - quantum number for the second 'radial' function in the eta-coordinate, eta=r-z ;

The principal quantum number n (which determines the eigenenergies) is related to the three above as

n = n1 + n2 + m + 1 .

For details consult the book by HA Bethe and EE Salpeter: Quantum Mechanics of One- and Two-Electron Atoms ; chapter 6. Just keep in mind that Bethe and Salpeter do not follow the usual convention for associated Laguerre polynomials, their  is really .

>	restart; Digits:=14:

>	with(plots):

Warning, the name changecoords has been redefined

We choose a value for the magnetic quantum number.

>

m:=0;

>	SE:=(E,Zp,f)->diff(s*diff(f,s),s)+(E/2*s-m^2/4/s+Zp)*f=0;

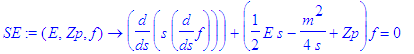
>	SE(E,Z1,f(s));

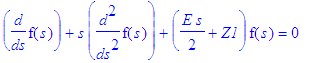
Here  s stands for either of the two parabolic coordinates, xi  or eta . For the pure Coulomb problem the two differential equations for the factors f1(xi)  and f2(eta)  are identical. This will change when we add an electric field along the z -axis.

Let us illustrate the meaning of the parabolic coordinates by drawing lines of constant xi  and eta  over the x - z  plane at y =0. This choice of plane really illustrates the rho - z  plane where rho  is the cylindrical coordinate measuring the distance from the rotation axis.

>	eq1:=sqrt(x^2+z^2)+z=c1;

>	eq2:=sqrt(x^2+z^2)-z=c2;

>	for i from 1 to 10 do:

>	PL1[i]:=implicitplot(lhs(eq1)=i*0.5,z=-5..5,x=-5..5,color=magenta,numpoints=5000); PL2[i]:=implicitplot(lhs(eq2)=i*0.5,z=-5..5,x=-5..5,color=green,numpoints=5000); od:

>	display([seq(PL1[i],i=1..10),seq(PL2[i],i=1..10)],scaling=constrained);

This plot shows that:

1) the coordinates are orthogonal; (in a scale-constrained plot the lines of constant xi/eta  intersect at right angles)

2) when the coordinates are varied from 0 to infinity they define a mesh that spans the x - z  plane; we use that plane at positive x  and rotate it by phi  about the z -axis. Then x  plays the role of cylindrical coordinate rho .

3) The nucleus will be placed at the origin of the coordinate system;

4) In addition to axial symmetry, the coordinate system is reflective of the left-right symmetry, but not of the spherical symmetry in the Coulomb problem.

Define the energy in terms of the principal quantum number and fix Z  - the nuclear charge. We also introduce a scale parameter epsilon  for the coordinates which changes with the energy.

>	En:=n->-Z^2/2/n^2;

>

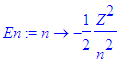
Z:=1;

>	epsilon:=n->sqrt(-2*En(n));

Now choose the principal quantum number:

>

n:=3;

>	En(n),epsilon(n);

Let us take the following attitude: we know the answers in sperical polar coordinates. Let us pick a certain principal quantum number n, we know the energy, let us then see which functions of eta and xi combined lead to allowed states (all for fixed m). The problem is now an eigenvalue problem in Z1.

>	simplify(SE(En(n),Z1,exp(-epsilon(n)*s/2)*s^(m/2)*f(s)));

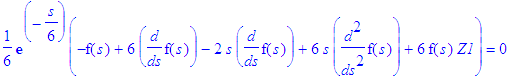
>	SE_1:=simplify(%/(s^(m/2)*exp(-s*epsilon(n)/2)));

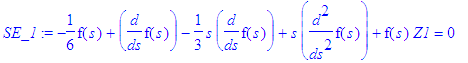
This equation can be made identical with the differential equation satisfied by the associated Laguerre polynomials.

Now pick a value for the n1  quantum number (starting at 0):

>

n1:=0;

We need the associated Laguerre polynomials:

>	LagA:=(n,k,x)->expand(((n+k)!)*add((-x)^m/(n-m)!/(k+m)!/m!,m=0..n));

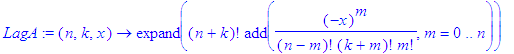
>	LagA(2,k,x);

Maple offers these as generalized Laguerre polynomials:

>	simplify(LaguerreL(2,k,x));

>	f||n1:=LagA(n1,m,epsilon(n)*s);

>	Z1:='Z1': simplify(subs(f(s)=f||n1,SE_1));

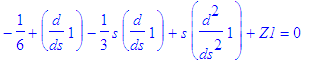
>	simplify(%); # weird: why do we need a repeat of simplify?

>	Z1:=solve(%,Z1);

>

Z2:=Z-Z1;

Can we find a solution for the second function with that value?

If Z2 = Z1  then we are done (the functions f1  and f2  will be identical and n1=n2 ).

If not, we have to find a solution with quantum number n2  such that Z2=Z - Z1  is satisfied.

Given that the equation for f2(eta)  is the same as for f1(xi)  let us proceed by finding the possible solutions for different values of n1 . At the end we will combine allowed states f1(xi)*f2(eta)  such that Z=Z1+Z2 .

Now step through the next possible solutions:

>

n1:=1;

>	f||n1:=LagA(n1,m,epsilon(n)*s);

We need to reset Z1  to the unassigned symbol so that we can solve for it.

>

Z1:='Z1':

>	simplify(subs(f(s)=f||n1,SE_1));

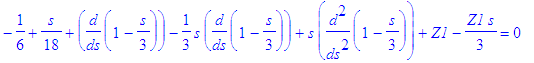
>	Z1:=solve(%,Z1);

This is not the one we need, but obviously we can combine Z1=1/2 with Z2=1/2.

Exercise 1:

For given Z=1  find all the possible values of {n1, Z1}  for n1=0,1,2,...  with Z1 < Z . These can be used to form combinations n1/n2  such that Z1+Z2=Z . Then investigate what happens for hydrogenlike atoms, e.g., Z=2 . Are there more allowed states?

>	f2:=LagA(2,m,epsilon(n)*s);

>

Z1:='Z1':

>	simplify(subs(f(s)=f2,SE_1));

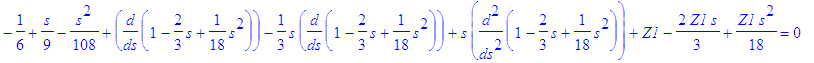
>	solve(%,Z1);

Thus, we have 3 candidates for m =0,   n =3:

{n1=0 , n2=2}, {n1=1 , n2=1}, {n1=2 , n2=0}

Three other states are possible at this level in the usual representation:

3s, 3p0, 3d0.

Now let us plot the density of the asymmetric state (2,0) [or (0,2)].

>	psi:=eval(exp(-epsilon(n)*s/2)*s^(m/2)*f2,s=xi)*eval(exp(-epsilon(n)*s/2)*s^(m/2)*f0,s=eta);

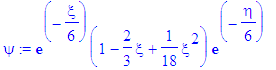
>	simplify(psi);

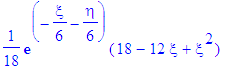
>	psi_1:=simplify(eval(psi,{eta=r-z,xi=r+z}));

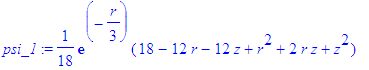
>	psi_1:=eval(psi_1,r=sqrt(x^2+y^2+z^2));

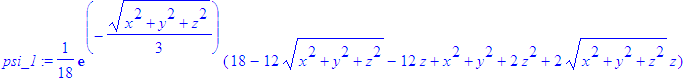
>	psi_1:=eval(psi_1,y=0);

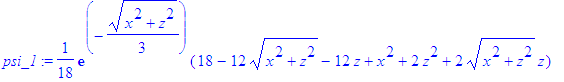
>	rho_1:=(psi_1)^2;

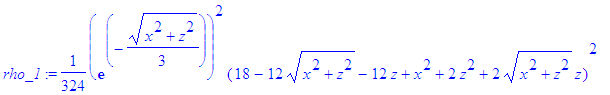
There are various ways to represent the probability (or charge) density:

We could simply graph the density over x  and z  (at y =0).

However, we are more interested in a graph that displays the probability to find the electron a certain distance along z  (that's the coordinate that did not get transformed, i.e., cylindrical z  = cartesian z ), and a distance x  away from the rotation axis. For the latter we include the Jacobian element in cylindrical coordinates, i.e., we show the distance x = rho  times the density.

>	plot3d(abs(x)*rho_1,x=-25..25,z=-25..25,axes=boxed,shading=zhue,style=patchcontour,numpoints=5000);

Now repeat for a symmetric state:

>	psi:=eval(exp(-epsilon(n)*s/2)*s^(m/2)*f1,s=xi)*eval(exp(-epsilon(n)*s/2)*s^(m/2)*f1,s=eta);

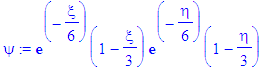
>	simplify(psi);

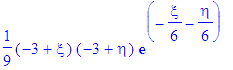
>	psi_1:=simplify(eval(psi,{eta=r-z,xi=r+z}));

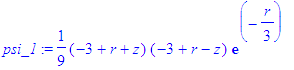
>	psi_1:=eval(psi_1,r=sqrt(x^2+y^2+z^2));

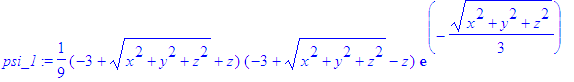
>	psi_1:=eval(psi_1,y=0);

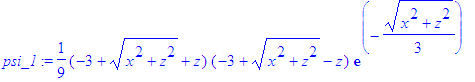
>	rho_1:=(psi_1)^2;

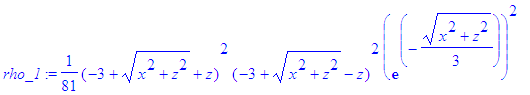
>	plot3d(abs(x)*rho_1,x=-25..25,z=-25..25,axes=boxed,shading=zhue,style=patchcontour,numpoints=5000);

This state's energy remains unaffected by an electric field along the z -axis. The contributions to the added potential energy expectation value at positive z  is cancelled by those from negative z .

Exercise 2:

Construct surface plots of the density for other states. Given a choice of n  and m , find the allowed n1/n2  pairs and graph the densities.

>