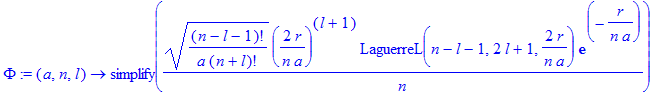
Hydrogenic positive-energy solutions

The E>0  solutions for the hydrogen atom problem represent scattering of electrons from protons. These states are defined for continuous energy E , and are therefore called continuum states to distinguish them from the bound states whose energy is discrete. States corresponding to continuous eigenenergies cannot be normalized in the usual way (cf. the plane-wave free-particle states).

We can gain some understanding of these solutions by first studying the Rydberg states, i.e., the high-lying bound states with E=-Z^2/(2*n^2) , e.g., for n>5 . The dependence of these eigenstates on the energy becomes very weak, because their eigenenergies approach zero. Following H. Friedrich: Theoretical Atomic Physics  (Springer-Verlag 1990) we graph them with a choice of normalization such that they all begin with equal slope at r=0 .

The bound states are defined as (Friedrich, Eq. 1.137):

>	restart: Digits:=14:

>	Phi:=(a,n,l)->simplify(sqrt((n-l-1)!/a/(n+l)!)/n*(2*r/n/a)^(l+1)*LaguerreL(n-l-1,2*l+1,2*r/n/a)*exp(-r/n/a));

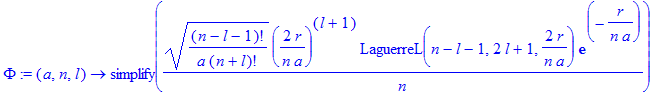
Note: without the simplify  command some parts below will calculate incorrectly (the derivatives of the Laguerre polynomials)!

Here the scale parameter for the distance is given as the Bohr radius a:

>	a0:=hbar^2/mu/(Z*e^2);

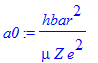
We introduce Bohr units in which the charge of the electron and its mass is set equal to unity, as is Planck's constant divided by 2*Pi . We introduce the reduced mass by approximating the proton mass as M=1836*m .

>	e:=1: hbar:=1: m:=1:

>	M:=1836: mu:=m*M/(m+M);

We select hydrogen (as opposed to a hydrogen-like ion), and check that the wavefunction defined above represents a radial orbital, Phi = r*Psi , which means that the normalization integral is to be carried out without the r^2  part of the volume element in spherical polar coordinates. The orbital is to be multiplied by a spherical harmonic to form the overall wavefunction.

>

Z:=1;

>	int(Phi(a0,3,2)^2,r=0..infinity);

Let us verify the eigenvalue problem for this state:

>	Hrad:=(phi,l)->simplify(-1/2/mu*diff(phi,r$2)/phi+l*(l+1)/(2*mu*r^2)-Z/r);

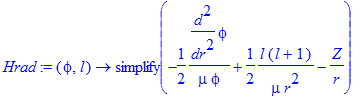
>	n0:=3: l0:=2: Hrad(simplify(Phi(a0,n0,l0)),l0);

>	simplify(-Z^2/2/3^2*mu);

Note how the radial Schroedinger equation involves two parts of the kinetic energy: the radial and centrifugal parts. The centrifugal part acts like a potential energy (very much like in classical mechanics we have an effective potential). Due to the knowledge of the angular parts as eigenfunctions of L^2 , namely the spherical harmonics, we have radial eigenvalue equations we predefined centrifugal potential that depends on the l  quantum number. The eigenvalue of L^2  is hbar^2*l*(l+1) .

Also note how the naive (infinite-mass proton) eigenvalue -Z^2/(2*n^2)  is multiplied by the reduced mass, and that the eigenenergy does not depend on the angular momentum quantum number. The latter part is a specialty of the pure Coulomb potential (accidental degeneracy related to the fact that there is an additional conserved quantity, the Runge-Lenz vector).

Exercise 1:

Verify the eigenvalue problem for other ( n , l ) eigenstates. Graph the radial probability densities for the chosen states. Superimpose on one graph the probability drawn over the baseline of the eigenenergy and the effective potential energy. Indicate the locations of the classical turning points.

Now we will normalize the radial functions differently, such that they will not allow a direct probabilistic interpretation, but will have comparable height of the first maxima and minima at small r  in the limit of large n . The Rydberg in our Bohr units is given as:

>	Ry:=hbar^2/mu/a0^2;

>	fn:=n->sqrt(n^3/2/Ry);

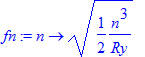
>	with(plots):

Warning, the name changecoords has been redefined

>

l0:=0;

>	P4:=plot(fn(4)*Phi(a0,4,l0),r=0..50*a0,color=red):

>	P5:=plot(fn(5)*Phi(a0,5,l0),r=0..50*a0,color=blue):

>	P6:=plot(fn(6)*Phi(a0,6,l0),r=0..50*a0,color=green):

>	P7:=plot(fn(7)*Phi(a0,7,l0),r=0..50*a0,color=brown):

>	P8:=plot(fn(8)*Phi(a0,8,l0),r=0..50*a0,color=magenta):

>	P9:=plot(fn(9)*Phi(a0,9,l0),r=0..50*a0,color=black):

>	P10:=plot(fn(10)*Phi(a0,10,l0),r=0..50*a0,color=yellow):

>

>	display(P4,P5,P6,P7,P8,P9,P10);

Why do the functions approach a limiting behavior at small r  ? The radial eigenvalue problem becomes the solution of the differential equation with eigenenergy E =0 approximately. This graph follows Fig. 1.5 in Harald Friedrich's book.

Exercise 2:

Repeat the above graph for higher values of angular momentum quantum number l . Why does the radial probability avoid the r =0 region for higher angular momentum values?

Now we let Maple solve the differential equation for us in the E =0 limit:

>	SE:=-1/2/mu*diff(u(r),r$2)+l*(l+1)/(2*mu*r^2)*u(r)-Z/r*u(r)=0;

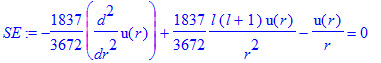
>	sol:=dsolve(SE);

>	nops(rhs(sol));

>	op(1,rhs(sol));

>	eval(op(1,rhs(sol)),{l=l0,_C1=1});

>	plot([eval(op(1,rhs(sol)),{l=l0,_C1=1}),eval(op(2,rhs(sol)),{l=l0,_C2=1})],r=0..50*a0,color=[red,blue],thickness=2);

We recognize that the second solution is not acceptable for small r , since it approaches a constant in the case of l =0. Thus the wavefunction itself is not finite.

We also recognize that in the high- n  limit the eigenfunctions become proportional to the E =0 solution found above.

We notice that the positive-energy solutions to the Schroedinger equation do not represent an eigenvalue problem in the same sense as for the bound states: we can fix the energy value (given that it is continuous, we can choose any value we want) and ask for the corresponding solution. Thus, we re-define the Schroedinger equation to allow for the positive energy value as an input parameter.

>	SE:=E->-1/2/mu*diff(u(r),r$2)+l*(l+1)/(2*mu*r^2)*u(r)-Z/r*u(r)-E*u(r)=0;

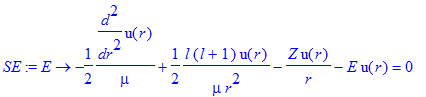
>	sol:=dsolve(SE(0.1));

We expect again that the solutions are made up of regular and irregular ones at the origin ( r =0), and that we will choose only the one with a finite probability at this point. The question of normalizability of this solution should now be addressed, and then we will graph the solutions for different energies to produce the equivalent of Fig. 1.6 in Theoretical Atomic Physics .

The first part of the solution represents a standing wave, which is regular at the origin. It can be made real by an imaginary choice of integration constant.

>	sol1:=eval(op(1,rhs(sol)),{_C1=-I,l=l0});

>	plot(sol1,r=0..50*a0,thickness=2);

The second part of the solution is irregular at the origin, and turns out to represent a travelling wave (it has out-of-phase real and imaginary parts:

>	sol2:=eval(op(2,rhs(sol)),{_C2=1,l=l0});

>	plot([Re(sol2),Im(sol2)],r=0..50*a0,color=[red,blue],thickness=2);

The E >0 solutions are usually expressed in terms of the confluent hypergeometric series. They are called Coulomb functions, and Appendix A4 in Friedrich's book provides a brief summary. The standard reference is M. Abramowitz and I.A. Stegun: Handbook of Mathematical Functions  (Dover 1970).

The positive-energy solutions are difficult to compute for Maple at large arguments, because they are obtained from a power series. They are not normalizable in the sense of bound states; they are not normalizable, i.e., they are not members of the usual Hilbert space of square-integrable functions L2. They can be delta-function normalized in the sense that <phi(E) | phi(E')>  is proportional to delta(E-E') . It is also possible to characterize them in terms of the wavenumber k  (with E=k^2/(2*mu) ), and to change the normalization condition to <phi(k) | phi(k')>  chosen to be proportional to delta(k-k') .

In the large- r  asymptotic regime the radial functions are chosen to behave like sin(k*r+gamma) . At these largest values of   r  both the centrifugal potential and the Coulomb potential vanish and the solution is obviously given by sine and cosine of k*r . The phase shift gamma  has some peculiarity due to the long-range nature of the Coulomb interaction.

We define the confluent hypergeometric series (it is also built into Maple in a more general form as hypergeom ). We truncate it at some finite order N.

>	F:=(a,b,z,N)->evalf(GAMMA(b)/GAMMA(a)*add(GAMMA(a+n)/GAMMA(b+n)*z^n/n!,n=0..N));

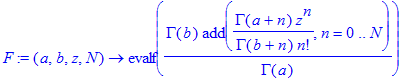
>	F(1,2,1.5,100);

>	hypergeom([1],[2],1.5);

We will use hypergeom , as it has a convergence check built into it.

>	eta:=-1/(k*a0);

>	Fl:=(k,l,z)->2^l*exp(Pi/(2*k*a0))/(2*l+1)!*abs(GAMMA(l+1-I/k/a0))*exp(-I*z)*z^(l+1)*hypergeom([l+1+I/k/a0],[2*l+2],2*I*z);

We should be ready for our graph now.

>	kE:=E->sqrt(2*mu*E);

The energy-normalized Coulomb functions are given as Eq. (1.150) in Friedrich:

>	FE:=(k,l,r)->evalf(sqrt(2*mu/Pi/hbar^2/k)*Fl(k,l,k*r));

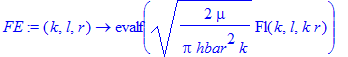
To generate the E=0 solution we select a small value of the energy:

>

s:=10;

>	P0:=plot(FE(kE(1E-5),l0,r),r=0..50*a0,thickness=2):

>	P1:=plot(0.1*s+FE(kE(0.1),l0,r),r=0..50*a0,color=blue,thickness=2):

>	P2:=plot(0.2*s+FE(kE(0.2),l0,r),r=0..50*a0,color=green,thickness=2):

>	P3:=plot(0.3*s+FE(kE(0.3),l0,r),r=0..50*a0,color=black,thickness=2):

>	display(P0,P1,P2,P3);

One notices the similarity of the continuum states for small r  where the energy balance is dominated by the Coulomb potential. The energy unit corresponds to 27.12 eV.

Exercise 3:

Generate the regular Coulomb solutions for higher angular momentum symmetries l >0 and compare the wavefunctions to the corresponding bound states of high n .

Asymptotic behavior:

The regular Coulomb functions have an asymptotic behavior which is parametrized in terms of a phase shift where the logarithmically divergent term is removed. The divergence arises as a result of the long-range nature of the Coulomb potential.

>	sigma:=(k,l)->evalf(argument(GAMMA(l+1-I/(k*a0))));

>	sigma(1,0);

>	Fas:=(k,l,r)->sqrt(2*mu/Pi/hbar^2/k)*sin(k*r+1/(k*a0)*log(2*k*r)-l*Pi/2+sigma(k,l));

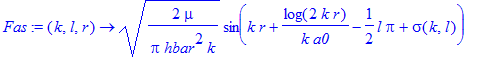
>	P1A:=plot(FE(kE(0.1),l0,r),r=50*a0..150*a0,color=blue):

>	P1a:=plot(Fas(kE(0.1),l0,r),r=50*a0..150*a0,color=magenta):

>	display(P1A,P1a);

>	eval([FE(kE(0.1),l0,r),evalf(Fas(kE(0.1),l0,r))],r=300);

>	eval([FE(kE(0.1),l0,r),evalf(Fas(kE(0.1),l0,r))],r=1000);

>

>	eval([FE(kE(0.2),l0,r),evalf(Fas(kE(0.2),l0,r))],r=1000);

The numbers are suspiciously close.

>	eval([FE(kE(0.4),l0,r),evalf(Fas(kE(0.4),l0,r))],r=1000);

>	eval([FE(kE(0.2),l0,r),evalf(Fas(kE(0.2),l0,r))],r=2000);

The asymptotic limit of the solution is reached at rather large values of r .

Exercise 4:

Check the validity of the asymptotic expression for different choices of angular momentum quantum number l  at different energies.

Verification of the solution

Now we compare the solution as stated above with the numerical solution of the Schroedinger equation.

The Schroedinger equation is formulated for a radial orbital which starts with psi(0)=0:

>	SE:=(E,l)->-hbar^2/(2*mu)*diff(psi(r),r$2)+(hbar^2/(2*mu)*l*(l+1)/r^2-Z/r-E)*psi(r)=0;

>

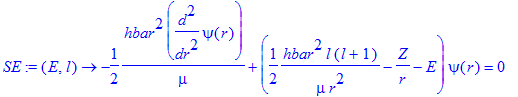
E0:=0.2;

>	SE(E0,l0);

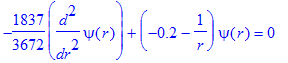
>	k0:=kE(E0);

We make a choice of initial condition which is compatible with the analytic solution:

>	zero:=1E-10;

>	FE(k0,l0,zero);

>	psi0:=Re(%);

>	FEp:=eval(diff(FE(k0,l0,r),r),r=zero);

>	psi0p:=Re(%);

>	IC:=psi(zero)=psi0,D(psi)(zero)=psi0p;

>	sol:=dsolve({SE(E0,l0),IC},numeric,output=listprocedure,maxfun=0):

>	Fnum:=eval(psi(r),sol):

>	Fnum(10),FE(k0,l0,10);

For a large value of r the numerical solution can be faster to evaluate than the analytical one. The power series for the hypergeometric function converges slowly for large arguments:

>	Fnum(1000);

>	FE(k0,l0,1000);

The imaginary part is an artefact.

This also raises the question of accuracy. How well do our solutions compare with the asymptotic anwer?

>	evalf(Fas(k0,l0,1000));

>	Fnum(5000),FE(k0,l0,5000),evalf(Fas(k0,l0,5000));

Warning, computation interrupted

The numerical solver works for large r  values only if the maxfun  option is set to iterate as long as required to reach the pre-set tolerance. The accuracy of the power series could be increased by an increase of the Digits  parameter. (This would slow down the numerical solver in dsolve , as it would no longer be using the floating point hardware of the CPU). For the given settings the convergence of the numerical solution to the asymptotic result has been demonstrated in the line above.

The numerical approach can be used for potentials that occur in models of many-electron atoms, where the pure Coulomb potential is replaced by a screened Coulomb potential for which no analytical solution can be found.

Exercise 5:

Verify the solutions for other energies and also for angular momentum symmetries l >0.

>

>

>