Stark resonance problem in parabolic coordinates

In this worksheet we investigate the problem of a hydrogen atom in an external DC electric field. We solve the problem in parabolic coordinates and learn that the bound-state spectrum 'disappears', and turns into a problem of resonances within a continuum of solutions at all energies.

This is an adaptation or extension of ideas originally put forward by HA Bethe and EE Salpeter in Quantum Mechanics of One- and Two-Electron Atoms , and followed up upon by Kolosov and Damburg in the late 1970ies in a series of papers in J.Phys. B.

>	restart; Digits:=14:

>	with(plots):

Warning, the name changecoords has been redefined

We choose a value for the magnetic quantum number.

>

m:=0;

>	SE1:=(E,Zp,f)->diff(xi*diff(f,xi),xi)+(E/2*xi-m^2/4/xi-F/4*xi^2+Zp)*f=0;

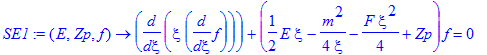
>	SE2:=(E,Zp,f)->diff(eta*diff(f,eta),eta)+(E/2*eta-m^2/4/eta+F/4*eta^2+Zp)*f=0;

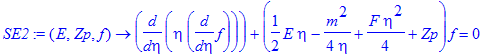
The problem is now to find two coupled solutions for the same energy E that satisfy Z1+Z2=Z = 1 .

We can gain some understanding by drawing the effective potentials. We divide by xi  and eta  respectively, the Zp -term becomes a Coulomb-type potential (we have a choice of how to split the charge between the uphill and downhill equations respectively.

F  is chosen to be small.

The representation of the effective potential is not exactly as indicated by Bethe and Salpeter. They remove a factor of sqrt(xi)  and sqrt(eta)  from the orbital to arrive at a simplified kinetic energy (just given as a second derivative) such that the radial equations really become the equivalents of the one-dimensional Schroedinger equations. We don't do this here to have a more straightforward boundary condition at xi=eta=0 . As a consequence the interpretation of the effective potentials Vup(xi)  and Vdown(eta)  is not as straightforward, but the idea is similar.

>	Vup:=xi->m^2/4/xi^2+F*xi/4-Z1/xi;

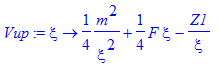
>	Vdown:=eta->m^2/4/eta^2-F*eta/4-Z2/eta;

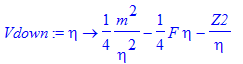
Our first look at the effective potentials is by splitting the charge Z=1  equally between both channels. After the determination of the charges Z1 and Z2 from solving the eigenvalue problem one can go back and look at the actual potentials. That is the purpose of the commented line below.

>	Z1:=1/2; Z2:=1-Z1;

>	#Z1:=Z_1; Z2:=Z_2;

>

F:=0.1;

>	plot([Vup(x),Vdown(x)],x=0..20,color=[red,blue],view=[0..20,-0.6..0.2],thickness=2);

Find out what happens to the ground state H(1s).

Without field the two potentials are identical, and we have the n1=0, n2=0  state. For non-zero F  we have to split Z1  and Z2  asymetrically to get a single eigenvalue in both equations. The strategy is to treat the problem as an eigenvalue problem in Z1/Z2  for given E .

One can proceed as follows: For a given energy below the barrier in the blue (downward channel) we solve the discrete eigenvalue problem in the upward channel for separation constant Z1 . That determines the downward potential ( Z2=Z-Z1 ). One can then solve the downward problem at known E,Z2 . For certain energies close to the bound states in the F=0  problem we should observe resonance channels.

What are the correct boundary conditions?

Taylor expansion about the origin: f(x)=f0+f1*x+f2*x^2  yields:

f1=-Z1*f0

f0  determines the normalization which is not essential for finding Z1 .

>	#E0:=-0.5274; # 1s-resonance position for F0=0.1

We avoid the origin vy defining an effective value for zero.

>	E0:=-0.5; zero:=1E-30:

We can get an idea for how far we should integrate, and where we can expect the up-channel wavefunction to vanish from solving for the classical turning points. The outer radius R should be larger than the outer turning point.

>	solve(E0=-0.5/z-F/4*z,z);

>

R:=30;

Now define a procedure which given a value for Z1  computes a solution to the up-channel, then returns the value of f1(xi)  for xi=R . This value will be made zero by the appropriate choice of Z1 .

>	Fzero:=proc(Z) local SE1t,IC,sol,F1; global R,m,E0,SE1,zero;

>	SE1t:=SE1(E0,Z,f1(xi));

>	IC:=f1(zero)=1,D(f1)(zero)=-Z;

>	sol:=dsolve({SE1t,IC},numeric,output=listprocedure):

>	F1:=eval(f1(xi),sol):

>	F1(R); end:

Try it out for some value:

>	Fzero(0.5);

Now determine Z1  restricting it to the range 0..1  for a start:

>	Z_1:=fsolve(Fzero,0..1);

The value is not too far from Z1=0.5  which is the  value for F=0 that corresponds to E=-0.5 , i.e the H(1s) ground state.

With the value of Z1  known we construct the solution in order to display it:

>	SE1(E0,Z_1,f1(xi));

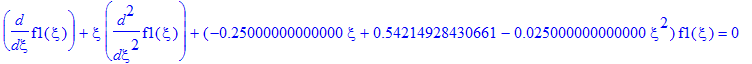
>	IC1:=f1(zero)=1,D(f1)(zero)=-Z_1;

Now run a trial value search for Z_1:

>	SE1t:=SE1(E0,Z_1,f1(xi));

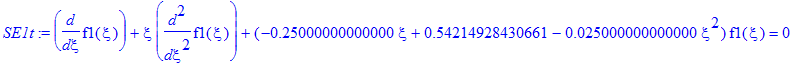
>	sol:=dsolve({SE1t,IC1},numeric,output=listprocedure):

>	F1:=eval(f1(xi),sol):

>	plot(F1(xi),xi=0..R-10,thickness=2);

The solution in the xi-coordinate is found to be nodeless ( n1=0 ).

Now solve the downward channel.

>	Z_2:=1-Z_1;

>	SE2t:=SE2(E0,Z_2,f2(eta));

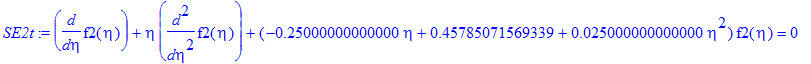
The initial condition is the same except for the different value of the charge:

>	IC2:=f2(zero)=1,D(f2)(zero)=-Z_2;

>	sol2:=dsolve({SE2t,IC2},numeric,output=listprocedure):

>	F2:=eval(f2(eta),sol2):

>	plot(F2(eta),eta=0..100,numpoints=1000,thickness=2);

What does this solution describe?

For small eta  the behavior of f2(eta)  is similar to f1(xi) , and looks similar to a H(1s) wavefunction. For larger eta  we obtain a standing wave with an amplitude that decreases slowly with increasing eta .

Even though this is not a travelling wave (neither inward nor outward) we can interpret the wavefunction as having two parts: a bound part at small eta , and a scattering-state which describes electrons removed from the atom. The two regimes are connected by a tunneling region. For weaker field strength F  and energies E0  close to the unperturbed ground state one should be able to see a region where the wavefunction is suppressed.

The wavefunction describes how in the eta-coordinate the electron is not confined to small distances, but can tunnel through the barrier.

Our real-valued solution does not describe an incoming or outgoing wave, but rather a standing wave. This is analogous to the pair of solutions {cos(k*x), sin(k*x)}  versus {exp(I*k*x), exp(-I*k*x)}  in the free-particle case.

The following is now of interest:

For a judicious choice of energy (remember: for scattering states we can choose E0  quite freely!) we will find solutions where the amplitude for the part trapped inside the potential barrier becomes comparable to (or perhaps even larger than) the outside freely travelling wave.

Exercise 1:

Explore what happens to the solution in the vicinity of E0=-0.5 . For the relatively large field strength of F=0.1  atomic units the character of the solution doesn't change too quickly with small variations in E0 . Find a value of E0  for which the amplitude in the outside region is minimized (compared to the small-eta amplitude which is fixed by the initial condition). At this energy a scattering electron is perfectly capable of tunneling into the small-eta region and forming a quasibound state. Eventually the resonant state decays again by tunneling. Explore the energy range for which the solution remains relatively stable. This will be indicative of the energy width of the resonance (usually denoted by Gamma ) which has the uncertainty relation property: Gamma*tau=hbar  (Planck's constant), where tau  is the lifetime of the resonance.

The proper treatment of this problem involves a trick by which the boundary conditions in the asymptotic regime force a square-normalizable wavefunction at the expense of a complex-valued energy E0 . For such solutions one can extract the resonance position as the real part of E0  (corresponds to the point at which our real-valued solution has maximum amplitude inside the barrier), and the imaginary part of E0  yields information about the lifetime of the trapped state.

>

We finish the worksheet by graphing the probability density in cylindrical coordinates (really in Cartesians in the y=0  plane, but one can rotate them about the z-axis)  

>	rV:=(x,z)->sqrt(x^2+z^2);

>	xiV:=(x,z)->rV(x,z)+z;

>	etaV:=(x,z)->rV(x,z)-z;

>	psi:=(x,z)->F1(xiV(x,z))*F2(etaV(x,z));

>	psi(1,1),psi(5,5);

The probability density is multiplied by the magnitude of x  which plays the role of polar cylindrical coordinate.

>	plot3d(log(abs(x)*psi(x,z)^2),x=-15..15,z=-20..10,axes=boxed,shading=zhue,style=patchcontour,numpoints=5000,orientation=[0,0]);

Exercise 2:

Observe how this probability density changes when the energy move away from the ground-state value of E0=-0.5 , e.g. to E0=-0.35 . What happens to the part located at [z=0, x=0] ? What happens when E0  approaches the unperturbed n=2  energy level E0=-0.125 ?

>

>