Morse oscillator

We look at the classical solution of the Morse oscillator. The periodic solutions for bound states are obtained numerically and decomposed into a Fourier series. One can see how for low energies the solutions are approximated well by a harmonic oscillator solution which has negligible Fourier components. For energies below the dissociation limit, but well above zero the anharmonicities are observed in the form of non-negligible Fourier coefficients.

In this regime of intermediate energies the classical model predicts that charged particles undergoing this type of motion can radiate directly at multiples of the fundamental frequency which is given by the inverse of the oscillation period. This corresponds in quantum mechanics to a direct spontaneous decay to an energy level below the neighboring one.

>	restart; Digits:=14:

>	V:=(1-exp(-q))^2;

>	plot(V,q=-1..5,thickness=3);

>	taylor(V,q=0);

>	F:=-diff(V,q);

>	NE:=diff(x(t),t$2)=eval(F,q=x(t));

>

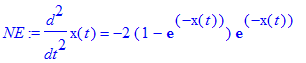
E0:=1/4;

>	q0:=fsolve(V(q)=E0);

>	sol:=dsolve({NE,x(0)=q0,D(x)(0)=0},numeric,output=listprocedure);

>	X:=eval(x(t),sol):

>	plot(X(t),t=0..20,thickness=2);

Let us calculate the Fourier coefficients numerically. For the given energy the period is known to be:

>	T:=E->evalf(2*Pi/sqrt(2*(1-E)));

>	T0:=T(E0);

>	a_n:=n->2/T0*evalf[10](Int(X(t)*cos(2*Pi*n*t/T0),t=0..T0,method=_Gquad));

>

a_n(0);

>

a_n(1);

>	A:=[seq(a_n(n),n=0..10)];

The Fourier-cosine coefficients converge rapidly to zero for increasing n.

Now show that the Fourier-sine coefficients vanish for our choice of periodicity interval:

>

>	b_n:=n->2/T0*evalf[10](Int(X(t)*sin(2*Pi*n*t/T0),t=0..T0,method=_Gquad));

>

b_n(1);

>	B:=[seq(b_n(n),n=1..10)];

The results tell us something about the precision of the calculations.

Thus, we assemble the Fourier-cosine series:

>	xF3:=t->0.5*A[1]+add(A[n+1]*cos(2*Pi*n*t/T0),n=1..3);

>	plot([X(t),xF3(t)],t=0..2*T0,color=[red,blue],thickness=2);

Indeed, with four coefficients we are getting close.

>	xF10:=t->0.5*A[1]+add(A[n+1]*cos(2*Pi*n*t/T0),n=1..10);

>	#qk:=k->((1-sqrt(1-E0))/sqrt(E0))^(2*abs(k))/k^2; #Fourier coefficients squared? (from paper)

>

A;

The acceleration (to be used in the Larmor formula)

>	aF10:=t->add(-(2*Pi*n/T0)^2*A[n+1]*cos(2*Pi*n*t/T0),n=1..10);

>	plot(aF10(t),t=0..2*T0,color=green,thickness=2);

>	n:=1; plot({seq([n,((2*Pi*n/T0)^2*abs(A[n+1]))^2*t,t=0..1],n=1..10)},color=blue,thickness=3);

It looks like the harmonics are too strong?

why did I take the squares?

what is the radiation proportional to?

Exercise 1:

Investigate the radiative spectrum for orbits of different energy. Observe how for low-energy orbits in the linear (nearly harmonic) regime the so-called harmonic motion involves oscillations at the fundamental frequency only. Make sure to understand the frequency spectrum also an energy spectrum according to E=h*f .

>

>

>