Time-dependent perturbation theory

We consider a finite-time monochromatic perturbation which connects an initially populated ground state to higher energy levels. We should keep in mind that a single-frequency sinusoidal signal when evaluated over finite times is not monochromatic at all, but experiences a broadening and other effects due to the pulse shape.

For simplicity we consider harmonic oscillator eigenstates.

>	restart; Digits:=14: with(plots):

Warning, the name changecoords has been redefined

>

w:=1;

>

m:=1;

>

hbar:=1;

>	En:=n->(n+1/2)*hbar*w;

>	with(orthopoly);

>	An:=n->1/sqrt(2^n*n!*sqrt(Pi));

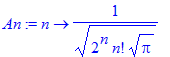
>	beta:=sqrt(m*w/hbar);

>	phi:=n->An(n)*exp(-beta^2*x^2/2)*H(n,beta*x);

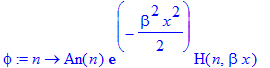
>	#plot([seq(phi(n),n=0..3)],x=-5..5,color=[red,blue,green,black],numpoints=500);

Normalization check:

>	int(phi(3)^2,x=-infinity..infinity);

Suppose the interaction represents a sinusoidally varying homogeneous electric field. The strength parameter lambda is unspecified, and the circular frequency of the field is called alpha.

>	W:=x*sin(alpha*t);

>	Wmat:=(m,n)->int(phi(m)*W*phi(n),x=-infinity..infinity);

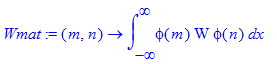
>	Wmat(0,1);

>	Wmat(0,2);

>	Wmat(0,3);

The interaction connects only states of opposite parity. This is obvious from the symmetry properties of the integrand.

From the calculation it also becomes clear that the interaction connects only neighboring levels. This is a special feature of the harmonic oscillator eigenfunctions.

Note that we have two frequencies in our problem: the harmonic oscillator frequency w=1, and the frequency of the field used to excite the system.

Let us make a choice for the frequency of the perturbation.

>	alpha:=w*0.999;

>	T_field:=2*Pi/alpha;

>

N_cyc:=3;

>	T:=N_cyc*T_field;

>	lambda:=0.1;

We parametrized the interaction matrix element in terms of time t. Therefore, we integrate over time t from 0 to s (which becomes our symbol for time after integration).

>	P_0k:=k->1/hbar^2*abs(lambda*int(exp(I*(En(k)-En(0))*t)*Wmat(0,k),t=0..s))^2;

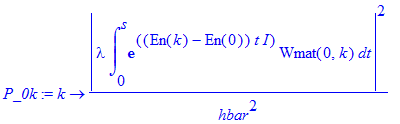
>	evalf(P_0k(1));

>	evalf(P_0k(3));

We store the graph for future reference. Note that we use s  as the time parameter.

>	PL1:=plot(P_0k(1),s=0..T,numpoints=500): display(PL1);

How should we interpret this result?

1) We can only excite the neighboring k=1  level in first-order perturbation theory. However, we should expect population of higher states as a result of second-order effects.

2) It appears as if the level will not only be excited, but also de-excited by the same matrix element. At the end of a complete cycle we find a complete return of the population back to the ground state.

Exercise 1:

Modify the frequency of the perturbation, i.e., choose alpha to be not as close to the resonance ( hbar*w  is the energy difference between neighboring levels, i.e., also between k=0  and k=1 ). Start with small deviations from resonance before you choose quite different circular frequencies for the 'laser pulse'. You will understand better what happens away from resonance in some of the work below.

The strong excitation results (on resonance) should make us suspicious about the usefulness of first-order PT in this problem. After all the zeroth-order result for c0(t)  was used, namely a probability of 1 in the original state throughout the interaction.

Let us attempt some second-order calculations for the population of the levels k=0,1,2 . For this purpose it is not sufficient to record the transition probabilities, but we need to keep track of the complex amplitudes.

To order O1 we have for the only non-vanishing excited-state probability amplitude:

>	c1_O1:=unapply(-I/hbar*int(exp(I*(En(1)-En(0))*t)*Wmat(0,1),t=0..s),s);

>	c0_O1:=1; # this is not very logical, as it is the result up to 1st order.

>	c2_O2:=unapply(-I/hbar*int(exp(I*(En(2)-En(1))*t)*Wmat(1,2)*c1_O1(t),t=0..s),s);

>	PL2:=plot(abs(lambda^2*c2_O2(t))^2,t=0..T,numpoints=500,color=blue): display(PL2);

>	c0_O2:=unapply(-I/hbar*int(exp(I*(En(0)-En(1))*t)*Wmat(1,0)*c1_O1(t),t=0..s),s);

>	PL3:=plot(abs(1+lambda^2*c0_O2(t))^2,t=0..T,numpoints=500,color=green): display(PL3);

The norm is not conserved well in the following sense: if we add the second-order probability for k=2  to the first-order probability for k=1  we have more probability than what was removed from unity in the elastic channel. This is why we may not want to use the actual probability calculation for the elastic channel, but rather assume that it is 1 - sum (excitation probabilities).

We now check the Fourier transform interpretation of the first-order result.

>

>	FT:=unapply(abs(int(exp(I*omega*t)*Wmat(0,1),t=0..N*2*Pi/omega))^2,omega,N);

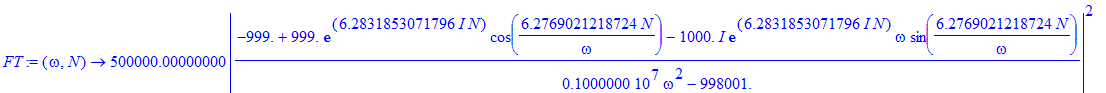
We show the frequency spectrum of the pulse for 10, 20, and 30 cycle-length pulses. The pulse shape profile is rectangular (square-wave modulation), i.e., sharp turn-on and turn-off.

>	plot([FT(omega,10),FT(omega,20),FT(omega,30)],omega=0.7*alpha..1.3*alpha,color=[red,blue,green]);

The sharp turn-on and turn-off of the monochromatic pulse at time 0  and time N*alpha  respectively causes a 'ringing' effect, namely the presence of sidebands around the center frequency. Note how broad the signal is for the number of cycles shown. The perturbation is very effective within this window, i.e., transitions will take place if the transition frequency between initial and final state is within the peak.

Think about the consequences: for a long pulse of thousands of cycles (or more) an effective excitation becomes possible only for small (or negligible) detuning from the resonance frequency.

Exercise 2:

Construct the Fourier transform of pulses containing more cycles. Read up on windowing functions in a reference text on discrete (fast) Fourier transforms to learn how they can suppress the ringing effect (e.g., Hanning window function, cf. digital oscilloscopes with FFT function). Realistic laser pulses do have pulse shapes with gradual turn-on and turn-off.

Now we solve the close-coupling equations. We connect only the levels k=0,1,2 .

>	Wmat(0,1);

>	Wmat(1,2);

>	DE0:=I*diff(c0(t),t)=lambda*add(c||j(t)*Wmat(0,j)*exp(I/hbar*(En(j)-En(0))*t),j=0..2);

>	DE1:=I*diff(c1(t),t)=lambda*add(c||j(t)*Wmat(1,j)*exp(I/hbar*(En(j)-En(1))*t),j=0..2);

>	DE2:=I*diff(c2(t),t)=lambda*add(c||j(t)*Wmat(2,j)*exp(I/hbar*(En(j)-En(2))*t),j=0..2);

>	IC:=c0(0)=1,c1(0)=0,c2(0)=0;

>	sol:=dsolve({DE0,DE1,DE2,IC},numeric,output=listprocedure);

>	C0:=eval(c0(t),sol): C1:=eval(c1(t),sol): C2:=eval(c2(t),sol):

>	PL4:=plot([abs(C1(t))^2,abs(C2(t))^2],t=0..T,color=[magenta,black]): display(PL2,PL1,PL4,title="Comparison of level populations P1(t)[magenta=close-coupling; red=TDPT] and P2(t)");

The three-channel close-coupling result is not exact, as it neglects couplings to the k=3  state. Given that the couplings proceed in steps, i.e., k=1  is populated from k=0 ; k=2 is populated from k=1 , etc. we expect this to affect the results at the latest times shown.

This feature of step-wise excitation also explains why the discrepancy between the first-order result for P1(t)  overestimates the close-coupling result by about the level of the P2(t)  calculated in second-order TDPT.

Note how the 2nd order result for P2(t)  agrees with the close-coupling calculation at times when the first-order answer for P1(t)  is overestimating the the corresponding TDSE result significantly.

Exercise 3:

Extend the close-coupling calculation to include couplings to the k=3  level. At what time do these populations become appreciable? What is the implication for the accuracy of the 3-channel ( k=0,1,2 ) close-coupling calculations shown above?

The philosophy in nth order TDPT is: use the probability amplitudes in previous order for the other levels to obtain the k-level correction at the order to be computed.

A few numerical comparisons:

>	abs(C0(T))^2+abs(C1(T))^2+abs(C2(T))^2;

>	evalf(eval(P_0k(1),s=T)),abs(C1(T))^2;

>	evalf(eval(P_0k(1),s=T/2)),abs(C1(T/2))^2;

>	evalf(eval(P_0k(1),s=T/4)),abs(C1(T/4))^2;

This raises the question:

to what order do we need to go in order to obtain agreement between the TDPT approach and the integration of the close-coupling equations not just at the beginning?

Let us try the higher-order result for the excitation of the k=1  state.

The scheme is to connect neighboring levels:

0->1 happens at O1

1->2 and 1->0  at O2. No contribution 0->1 at this level because the 1st order contribution to the c1(t) coefficient vanishes.

So let us calculate the 3rd order contribution to c1(t).

>	c1_O3:=unapply(-I/hbar*(int(exp(I*(En(1)-En(0))*t)*Wmat(0,1)*c0_O2(t),t=0..s)+int(exp(I*(En(1)-En(2))*t)*Wmat(2,1)*c2_O2(t),t=0..s)),s);

>

c1_O3(1);

>	plot([abs(C1(t))^2,abs(lambda*c1_O1(t))^2,abs(lambda*c1_O1(t)+lambda^3*c1_O3(t))^2],t=0..T,numpoints=500,color=[magenta,red,brown],title="P1(t): CC[magenta], TDPT-O1[red], TDPT-O3[brown]");

One can see that the TDPT result up to third order follows the close-coupling result very well. At late times the third-order correction overcompensates the large deviation in the first-order result.

One can view the TDPT scheme as a successive approximation scheme that integrates the system of ordinary differential equations (the CC equations form of the TDSE) in a successive approximation scheme.

Exercise 4:

The calculation of c1_O3(t)  represents the complete pattern of the TDPT scheme for the present problem. Nearest neighbors are connected by the perturbation. One uses the coefficients from the previous approximation (not the complete coefficient, just the contribution from that order!) multiplies it with the appropriate coupling matrix and computes the Fourier transform for fixed transition frequency.The two amplitudes from the lower-lying and higher-lying neighboring energy levels are added coherently to form the overall probability amplitude. Use this pattern to compute the population P1(t)  at the next order for which there is a non-trivial contribution.

We proceed with an improved calculation of the probability to remain in the ( k=0 ) ground state. In this case there is only one contribution, as the connection is only to the k=1  state. We have contributions at order lambda^2  and lambda^4  which can be calculated from the known results for c1  at orders O1 and O3. The O2 result is known already:

>

c0_O2(1);

>	c0_O4:=unapply(-I/hbar*int(exp(I*(En(0)-En(1))*t)*Wmat(1,0)*c1_O3(t),t=0..s),s);

>

c0_O4(1);

>	plot([abs(C0(t))^2,abs(1+lambda^2*c0_O2(t))^2,abs(1+lambda^2*c0_O2(t)+lambda^4*c0_O4(t))^2],t=0..T,numpoints=500,color=[magenta,red,brown],title="P0(t): CC[magenta], TDPT-O2[red], TDPT-O4[brown]");

We can observe the impressive agreement between the CC result and the O4-TDPT result for the elastic channel. If the system were evolved for a longer time, or for stronger coupling lambda we should observe that TDPT at high order will converge against the CC result with more equations coupled than in the present case.

One should keep in mind that the coupling scheme is particularly simple for the harmonic oscillator. For anharmonic potentials direct coupling to more excited states is possible by the time-dependent linear potential.

Mini-project:

Explore what happens to the above results when the strength parameter lambda is increased (e.g., doubled, etc.). Be careful in your interpretation of results. Note when the calculated probability expression exceeds unity and understand what this means. Extend the CC equations to sufficient matrix dimension to guarantee converged results against which the TDPT calculations are compared.

>

>

>