MacKenzie, I. S. (2002). KSPC (keystrokes per character) as a characteristic of text entry techniques. Proceedings of the Fourth International Symposium on Human Computer Interaction with Mobile Devices (LNCS 2411), pp. 195-210. Heidelberg, Germany: Springer-Verlag. [software]
KSPC (Keystrokes per Character) as a Characteristic of Text Entry Techniques
I. Scott MacKenzie
Dept. of Computer ScienceYork University
Toronto, Ontario, Canada M3J 1P3
smackenzie@acm.org
Abstract
KSPC is the number of keystrokes, on average, to generate each character of text in a given language using a given text entry technique. We systematically describe the calculation of KSPC and provide examples across a variety of text entry techniques. Values for English range from about 10 for methods using only cursor keys and a SELECT key to about 0.5 for word prediction techniques. It is demonstrated that KSPC is useful for a priori analyses, thereby supporting the characterisation and comparison of text entry methods before labour-intensive implementations and evaluations.
1 Introduction
An important research area in mobile computing is the development of efficient means of text entry. Interest is fueled by trends such as text messaging on mobile phones, two-way paging, and mobile web and email access. Coincident with this is the continued call in HCI for methods and models to make systems design tractable at the design and analysis stage [5]. This paper addresses these two themes. We propose a measure to characterise text entry techniques. It is calculated a priori, using a language model and a keystroke-level description of the technique. The measure is used to characterise and compare methods at the design stage, thus facilitating analyses prior to labour-intensive implementations and evaluations.
2 Keystrokes Per Character (KSPC)
KSPC is an acronym for keystrokes per character. It is the number of keystrokes required, on average, to generate a character of text for a given text entry technique in a given language. That KPSC ≠ 1 for certain text entry techniques has been noted before [e.g., 1, 7, 8]. The contributions herein are (i) to systematically describe the calculation of KSPC, (ii) to provide examples of KSPC over a wide range of text entry techniques, some with KSPC > 1, others with KSPC < 1, and (iii) to demonstrate the utility of KSPC as a tool for analysis.
Although we write "keystrokes", KSPC also applies to stylus-based input, provided entry can be characterised by primitives such as strokes or taps.
3 Qwerty Keyboard (KSPC = 1)
The ubiquitous Qwerty keyboard serves as a useful baseline condition for examining KSPC. First, considering just lowercase letters, we note that the Qwerty keyboard is unambiguous because each letter has a dedicated key. In other words, each keystroke generates a character of text. Given this, we conclude the following for the basic Qwerty keyboard:
| KSPC = 1.0000 | (1) |
Of course, the value edges up slightly if we consider, for example, shift key usage. However, this is a good start. The process is not as simple for other keyboards and techniques, however. There are two central requirements in computing KSPC. The first is a clear keystroke-level description of the entry technique. This we provide as each technique is presented. The second is a language model. This is needed to normalize KSPC, so it is an "average", reflecting both the interaction technique and the user's language.
4 Language Model
A language model is built using a representative body of text – a corpus. We used the British National Corpus (ftp.itri.bton.ac.uk/bnc) which contains about 90 million words.1 Since the corpus is rather large, we used forms more easily managed, yet suited to our needs. We used three such forms of the corpus.
4.1 Letters and Letter Frequencies
In the most reduced form, we work only with letters. The result is a small file (< 1KB) with 27 lines, each containing a letter (SPACE, a-z) and its frequency. The frequencies total 505,863,847. The first five entries are
_ 90563946 a 32942557 b 6444746 c 12583372 d 16356048
The SPACE character ('_') is the most prevalent, representing about 18% of all input in text entry tasks (see also [10]). Punctuation and other characters were excluded for a few reasons. In particular, they are problematic because the method of entry is not standardized and is typically dependent on the implementation, rather than on the technique per se.
If the keystrokes for an entry technique are appended to each entry in the letter-frequency file, then KSPC is computed as follows:
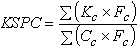
| (2) |
where Kc is the number of keystrokes required to enter a character, Cc = 1 (the 'size' of each character), and Fc is the frequency of the character in the corpus.
Although small and efficient, the letter-frequency form of the corpus is useful only if the entry of each character depends only on that character. If the keystrokes also depend on neighboring characters (as demonstrated later), then a more expansive form is required.
4.2 Digrams and Digram Frequencies
The digram form of the corpus contains 27 × 27 = 729 entries. Each contains a digram – a two-letter sequence – and its frequency. The frequency is the number of times the second letter occurred immediately following the first. The frequencies again tally to 505,863,847. The five-most-frequent digrams are
Equation 2 still applies if the digram table is used. The only difference is that summation occurs over 729 entries, rather than 27.e_ 18403847 _t 14939007 th 12254702 he 11042724 s_ 10860471
The digram table is reasonably small (8KB) and it is useful if the keystrokes to enter a character depend on the preceding character. However, it falls short if the keystrokes depend on more than one preceding character, as demonstrated later.
4.3 Words and Word Frequencies
In the word form, the corpus is reduced to a list of unique words. The result is a file of about 1MB containing 64,566 words with frequencies totaling 90,563,946. The top five entries are
the 6187925 of 2941789 and 2682874 to 2560344 a 2150880
Not surprisingly, 'the' is the most common word with 6,187,925 occurrences. Our list extends down to words with as few as three occurrences. Weighted by frequency, the average word size is 4.59 characters. A variation on this list containing 9025 entries was used by Silfverberg et al. [9] in their study of text entry on mobile phones.
For each word, we determine the keystrokes to enter the word in the interaction technique of interest. With this information, KSPC is computed as follows:
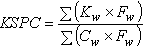
| (3) |
where Kw is the number of keystrokes required to enter a word, Cw is the number of characters in the word, and Fw is the frequency of the word in the corpus. Importantly, Kw and Cw are adjusted to include a terminating SPACE after each word.
We begin by examining text entry techniques requiring more than one keystroke per character.
5 Keypads (KSPC > 1)
In mobile computing, full-size Qwerty keyboards are generally not practical. Alternate text entry techniques are employed such as handwriting recognition, stylus tapping on a soft keyboard, or pressing keys on miniature keypads. Since the keypad devices often have fewer keys than symbols in the language, more than one keystroke is required for each character entered.
5.1 Date Stamp Method
The date stamp method can be implemented with three keys: LEFT and RIGHT cursor keys and a SELECT key. It is so named because of similarity to a teller's date stamp, where characters are found by rotating a wheel containing the entire character set. As a text entry method, we assume the arrow keys maneuver a cursor over a linear sequence of letters and a SELECT key enters a letter. Players of arcade games know this technique, as it is often used to add one's name to a list of high scorers.
The date stamp method is well characterised by KSPC. We considered four variations, combining two character arrangements with two cursor behaviours. A good start is just to arrange letters alphabetically with a SPACE at the left:
Interaction proceeds by moving a cursor back and forth with the arrow keys and entering characters by pressing the SELECT key. We call this date stamp method #1._abcdefghijklmnopqrstuvwxyz
With the LEFT, RIGHT and SELECT keys operating as just described, we can append the requisite keystrokes to each entry in the digram-frequency table. The first five entries are as follows:
So, entering SPACE after 'e' requires six keystrokes (LLLLLS), a very frequent act in English. With a full digram table as above, KSPC is computed using Equation 2:e_ 18403847 LLLLLS _t 14939007 RRRRRRRRRRRRRRRRRRRRS th 12254702 LLLLLLLLLLLLS he 11042724 LLLS s_ 10860471 LLLLLLLLLLLLLLLLLLLS
| KSPC = 10.6598 | (4) |
In method #1, the cursor is persistent: It maintains its position after each character entered. Since SPACE occurs with the greatest frequency in text entry tasks, it is worth considering a snap-to-home mode, whereby the cursor jumps to the SPACE character after each character entered. We call this method #2. Thus, inputting a SPACE requires just one keystroke, regardless of the preceding character. The improvement is only slight, however:
| KSPC = 10.6199 | (5) |
Another possibility is to position the SPACE character in the middle of the alphabet:
Thus, SPACE is well-situated for English text entry. This letter arrangement combined with a persistent cursor bears further improvement (method #3):abcdefghijklm_nopqrstuvwxyz
| KSPC = 9.1788 | (6) |
However, a good leap forward is produced by combining a central SPACE character with a snap-to-home cursor (method #4):
| KSPC = 6.4458 | (7) |
English text is produced with about 40% fewer keystrokes per character using method #4 than using method #1. Numerous variations of the date stamp methods are possible, such as multiple SPACE characters, clustering common letters (e.g., 'e', 'a', 't') near the home position, or using linguistic knowledge to dynamically rearrange letters after each input to minimize the cursor-key distance to the next letter. Space precludes further elaboration here.
This simple exercise with the date stamp method illustrates the value of KSPC for a priori analyses of prospective text entry techniques. While avoiding labour-intensive implementations or evaluations, the exercise provided a reasonable sense of the outcome. One assumption is that KSPC is related to text entry throughput, for example, in "words per minute", and this seems reasonable. This is discussed in more detail later.
5.2 5-button Pager Keypad
There are no commercial examples of the date stamp method in mobile computing. Conversely, 5-button text entry is a reality on low-end two-way pagers. An example is the AccessLink II by Glenayre (www.glenayre.com). This device has an LCD display and five buttons for text entry (see Figure 1).
The five buttons are for LEFT, RIGHT, UP, and DOWN cursor control and SELECT. The display contains four lines of 20 characters each. When entering a message, the top line displays the message, and the bottom three lines present a virtual keyboard. The portion of the virtual keyboard of interest here is shown in Figure 2.
Fig. 1. Five-button pager keypad
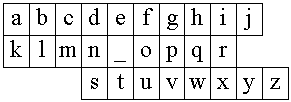
Fig. 2. Letter positions on the
Glenayre pager virtual keyboard
Note the central position of the SPACE character ('_'), and its proximity to 'e', the most common letter in English. Text is entered by maneuvering the cursor with the arrow keys and entering letters with the SELECT key. On the Glenayre pager, the cursor snaps to a home position over the SPACE character after each entry. Since snap-to-home is used, keystrokes depend only on the current character, and so, the letter-frequency version of the corpus is sufficent to compute KSPC. A brief excerpt follows:
Entering text via the soft keyboard in Figure 1 as just described yields_ 90563946 S a 32942557 ULLLLS b 6444746 ULLLS ... y 7929073 DRRRRRS z 221512 DRRRRRRS
| KSPC = 3.1320 | (8) |
This is about 50% fewer keystrokes per character than for date stamp method #4.
As with the date stamp methods, a variety of design alternatives are possible. See [1] for examples of techniques for linguistic optimization.
5.3 12-Key Mobile Phone Keypad
From three, to five, to twelve keys, mobile phones are better equipped for text entry than the devices just discussed; however, a significant challenge remains due to ambiguity in the keys (see Figure 1).
The letters a-z are spread across the keys 2-9 with 0 or # used for SPACE. The various methods for entering text using a 12-key keypad can be characterised by KSPC.
Multitap
Multitap is the conventional method for programming a mobile phone's address book. It is also widely used for entering text messages.

Fig. 3. Encoding of letters on a mobile phone keypad
With multitap, the user presses each key one or more times to specify the desired letter. For example, '2' is pressed once for 'a', twice for 'b', three times for 'c'. Multitap interaction can be accurately laid out in a digram-frequency file, however the examples are more interesting in the word form, so we'll use these here. The top five entries in the word-frequency file appear as follows, with multitap keystrokes appended:
So, 'the' is entered as 8-4-4-3-3-S, where 'S' = SPACE.the 6187925 84433S of 2941789 666333S and 2682874 2663S to 2560344 8666S a 2150880 2S
Besides requiring multiple keystrokes for many letters, a mechanism is required to segment consecutive letters on the same key. The preferred technique is to press a special NEXT key between conflicting letters (see [9] for further details). As an example, our multitap word-frequency file includes the following entry for 'this':
Since 'h' and 'i' are both on the 4 key, NEXT is pressed to separate them. Note that 12 keystrokes produced a four-letter word. Assuming the word is followed by a space, we have KSPC = 12 / (4 + 1) = 2.4. Of course, a better measure is obtained by processing the entire file, as per Equation 3. Given this, we compute the following for English text entry using multitap mode on a mobile phone keypad:this 463239 844N4447777S
| KSPC = 2.0342 | (9) |
Although a clear improvement over the pager method, this is still more than double our baseline of KSPC = 1.0000 for Qwerty. Not surprisingly, alternate text entry methods using the mobile phone keypad have emerged.
Dictionary-based Disambiguation
Commercial telephone answering systems sometimes prompt the caller to enter the name of the person they wish to contact. The name is spelled by pressing the keys bearing the letters of the person's name. Each key is pressed just once. Thus, referring to Figure 1, 'smith' is entered as follows: (For clarity, letters are also shown.)
7 6 4 8 4 s m i t h
Although the key sequence 7-6-4-8-4 has 4 × 3 × 3 × 3 × 3 = 324 renderings (see Figure 3), most are nonsense. The correct entry is found by searching a database for an entry matching the inputted key sequence. This technique is called dictionary-based disambiguation. Clearly, it also has potential for general-purpose text entry on a mobile phone. Examples include T9 by Tegic (www.tegic.com), eZiText by Zi (www.zicorp.com), or iTAP by Motorola (www.motorola.com/lexicus). T9 is the most widely used at the present time.
Of course the technique has limitations. If more than one word matches a key sequence, then the most probable is offered first. Alternatives appear by decreasing probability and are selected by successive presses of the NEXT key. A few examples from our word-frequency file illustrate this:
The first four words above have the same key sequence: 2-2-5-3. 'able' – the most probable – is the default. If 'cake', 'bald', or 'calf' is intended, then one, two, or three presses of NEXT are required, respectively. Note that keystroke descriptions are not possible using letter- or digram-frequency files, because NEXT-key usage depends on the entire word, not just on the preceding letter.able 26890 2253S cake 2256 2253NS bald 569 2253NNS calf 561 2253NNNS calendar 1034 22536327S
Given a complete keystroke rendering of the word-frequency entries, as above, KSPC for dictionary-based disambiguation is thus calculated:
| KSPC = 1.0072 | (10) |
This is very close to 1.0000, suggesting presses of NEXT are relatively rare with dictionary-based disambiguation. The keystroke overhead above is only 0.72%, or about one additional keystroke every 1 / 0.0072 = 139 keystrokes. Assuming five characters per word, this is equivalent to about one additional keystroke every 139 / 5 = 27.8 words. Note that the most probable word in any ambiguous set (e.g., 'able' above) is the default and is entered directly, without pressing NEXT.
However impressive the KSPC figure above is, it is predicated on the rather generous assumption that users only enter dictionary words. It is well known that text messaging users employ a rich dialect of abbreviations, slang, etc. [4], and, in view of this, many systems allow users to enter new words in a dictionary. However, when confronted with non-dictionary words, dictionary-based disambiguation fails, and the user's only recourse is to switch to an alternate entry mode, such as multitap.
Prefix-based Disambiguation
To avoid the problem just noted, Eatoni Ergonomics (www.eatoni.com) developed an alternative to dictionary-based disambiguation. Their method, called LetterWise, uses prefix-based disambiguation [7]. Instead of using a stored dictionary to guess the intended word, LetterWise uses probabilities of "prefixes" in the target language to guess the intended letter. A prefix is simply the letters preceding the current keystroke. Implementations currently use a prefix size of three. For example, if the user presses the 3 key with prefix '_th', the intended next letter is quite likely 'e' because '_the' in English is far more probable than '_thd' or '_thf'.The distinguishing feature is that prefix-based disambiguation does not use a dictionary of stored words: it is based on the probabilities of letter sequences in a language. Thus, the technique degrades gracefully when confronted with unusual character sequences, as in abbreviations, slang, etc. Switching to an alternate entry mode is not needed.
Still, the wrong letter is occasionally produced, and in these cases the user presses the NEXT key to choose the next mostly likely letter for the given key and context.
The following is a brief excerpt from the word-frequency file, with LetterWise keystrokes appended:
Given a complete rendering of the word-frequency file, as above, the following KSPC measure results for prefix-based disambiguation, as typified by LetterWise:the 6187925 843S of 2941789 63S and 2682874 263S ... hockey 601 4N62NN539S ecology 601 3NN2N65649S
| KSPC = 1.1500 | (11) |
Thus, the overhead is just 15% above KSPC = 1.0000 for Qwerty. This is well below the same figure for multitap (103%). Although the comparison with dictionary-based disambiguation is less impressive, the KSPC figure for LetterWise does not carry the same assumption with respect to dictionary words.
Other Keypad-based Techniques
Other input techniques have been proposed for the 12-key keypad. One example is MessagEase from EXideas (www.exideas.com), which we include here to round out our KSPC measures for 12-key keypads. With MessagEase, the modified keypad shown in Figure 4 is used.Digits are entered in the usual way, by pressing the corresponding key. For text entry, the alphabet is arranged by dividing letters into three sets. For the nine most-common letters (anihortes), the corresponding key is pressed twice (e.g., 4-4 for 'h'). For the next-most-common letters (upbjdgcq), the 5 key is pressed first followed by the key "pointed to" by the letter (e.g., 5-3 for 'p'). For the least-common letters (vlxkmywf) the corresponding key is pressed followed by the 5 key (e.g., 4-5 for 'k'). To enter a SPACE, 0 is pressed once.
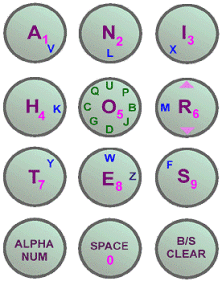
Fig. 4. MessagEase keypad
MessagEase keystrokes can be accurately expressed using a letter- or digram-frequency form of the corpus; however, as before, the word-frequency form is more interesting. The following is a brief excerpt showing MessagEase keystrokes:
Since each letter requires precisely two keystrokes, except SPACE which is pressed once, the KSPC measure for MessagEase is not surprising:the 6187925 774488S of 2941789 5595S and 2682874 112258S ... hockey 601 445554458875S ecology 601 88545525555775S
| KSPC = 1.8210 | (12) |
We now shift our focus to text entry techniques at the other end of the KSPC continuum ¾ those requiring less than one keystroke per character of text entered.
6 Word Prediction (KSPC < 1)
With word prediction, there is the potential for KSPC < 1 because words can be entered without explicitly entering every letter. Given a sufficient portion of a word to identify it in a dictionary, an interaction technique is invoked to select the full word and deliver it to the application.
To explore KSPC for text entry techniques using word prediction, we must decide on interaction details, such as the input method, generation of the list of candidate words, and modeling the keystroke overhead in selecting the intended word from the candidate list.
For the analyses presented here, we assume an input method such as unistroke recognition, stylus tapping on a soft keyboard, or pressing keys on a miniature Qwerty keyboard. So, KSPC = 1 as entry progresses. Word prediction joins in as follows. A list of candidate words is produced as each letter is entered. The size of the list is a variable, n. If n = 1, only a single predicted word is offered, much like word completion in spreadsheets or URL completion in web browsers. If n > 1, the list contains the n most-frequent words beginning with the current word stem. The most-frequent word is first in the list, and so on. If the intended word appears, it is selected using a specified technique. This description is consistent with commercial examples, such as WordComplete by CIC (http://www.cic.com/). Given this, the number of keystrokes to enter the word is determined. This process is repeated for every word in the dictionary, and KSPC is computed as described earlier.
The number of keystrokes to enter a word has two components: (i) the number of characters in the word stem at the point where the intended word appears in the candidate list, and (ii) the keystroke overhead to select the intended word in the candidate list.
The keystroke overhead depends on the entry method. In our analyses, we consider two methods: stylus input and keypad input. With stylus input, the overhead is just 1 keystroke to tap on the intended word in the candidate list. The tap selects the word and adds a SPACE.
With keypad input, some effort is required to reach the intended word in the candidate list and to select it. The keystroke overhead is the lesser of (i) the number of characters remaining in the intended word, or (ii) the index of the intended word in the candidate list; plus one further keystroke to select the word and append a SPACE.
Two examples will help. If the user is entering 'vegetable' and n = 5, then the word stem and the candidate list after each keystroke are as follows:
| Word Stem | Candidate List a |
|---|---|
| v | very voice view value various |
| ve | very version vehicle vehicles versions |
| veg | vegetables vegetation vegetable vegetarian vegetarians |
| a based on 64,566 word British National Corpus | |
The intended word appears with the word stem 'veg' as the third entry in the candidate list. Although 'vegetable' followed by SPACE suggests 9 keystrokes, word prediction offers a savings. If stylus input is used, 4 keystrokes (viz. stylus taps) are required: 3 to enter the word stem, plus 1 to select the word from the candidate list and add a terminating SPACE.
If keypad input is used, 6 keystrokes are required: 3 to enter the word stem, plus 2 presses of NEXT to reach the intended word (because it is 3rd in the candidate list), plus 1 to select the word and add a SPACE. Thus,
One further example illustrates the "lesser of " proviso noted above for keypad input. Consider the word 'active' which normally requires 7 keystrokes (including SPACE). With word prediction, the following interaction ensues:vegetable 979 vegS(stylus input, n = 5)
vegetable 979 vegNNS(keypad input, n = 5)
| Word Stem | Candidate List a |
|---|---|
| a | and a as at are |
| ac | act actually across action account |
| act | act actually action activities activity |
| acti | action activities activity active actions |
| a based on 64,566 word British National Corpus | |
The intended word appears with the word stem 'acti' as the fourth entry in the candidate list. With stylus entry the word is entered with 5 keystrokes: 4 to enter the word stem, plus 1 to tap on the word in the candidate list.
However, the situation is less clear with keypad input. Potentially, 8 keystrokes are needed: 4 for the word stem, plus 3 to reach the intended word in the list, plus 1 to select the word. Or, the user could just finish entering the word in the usual manner: 7 keystrokes. Although intermediate strategies are possible, such as waiting for a word to rise in the list as more letters are entered, the impact on KSPC is minimal. For this analysis we assume the user acts when (or if) a word first appears in the candidate list, and that the user takes the best option – the lesser of the two tallies. Thus,
We calculated KSPC as just described for keypad and stylus input with four sizes of candidate lists:active 7290 actiS(stylus input, n = 5)
active 7290 activeS(keypad input, n = 5)
keypad n = 1 KSPC = 0.7391 (13) keypad n = 2 KSPC = 0.7086 (14) keypad n = 5 KSPC = 0.7483 (15) keypad n = 10 KSPC = 0.8132 (16) stylus n = 1 KSPC = 0.7391 (17) stylus n = 2 KSPC = 0.6466 (18) stylus n = 5 KSPC = 0.5506 (19) stylus n = 10 KSPC = 0.5000 (20)
With keypad or stylus input, KSPC = 0.7391 at n = 1, thus illustrating the potential benefit of word prediction text entry techniques. For keypad input, there is a slight gain at n = 2 (KSPC = 0.7086); however, there is a net loss at n > 2. In other words, the keystroke overhead in reaching and selecting candidate words more than offsets the gain afforded by word prediction.
For stylus input, just the opposite occurs: as n increases, KSPC decreases. The best result is KSPC = 0.5000, coincident with n = 10. Since the overhead is fixed at 1 tap with stylus input, increasing the size of the list always reduces KSPC, albeit with diminishing returns.
KSPC does not reveal the full picture with predictive interfaces or other interaction techniques for text entry. Some key performance issues are examined next.
7 Comparison of Text Entry Methods
The methods discussed above appear in Table 1, sorted by decreasing KSPC. KSPC varies by a factor of 20, from 0.5 for stylus input with word prediction using ten candidate words, to just over 10 for date stamp method #1. Midway is our Qwerty condition of KSPC = 1.0000.
Comparison of Text Entry Methods
| Interaction Technique | KSPC |
|---|---|
| Date Stamp (#1) | 10.6598 |
| Date Stamp (#2) | 10.6199 |
| Date Stamp (#3) | 9.1788 |
| Date Stamp (#4) | 6.4458 |
| Pager | 3.1320 |
| Multitap | 2.0342 |
| MessagEase | 1.8210 |
| LetterWise | 1.1500 |
| T9 | 1.0072 |
| Qwerty | 1.0000 |
| Word Prediction (keypad, n = 10) | 0.8132 |
| Word Prediction (keypad, n = 5) | 0.7483 |
| Word Prediction (keypad, n = 1) | 0.7391 |
| Word Prediction (stylus, n = 1) | 0.7391 |
| Word Prediction (keypad, n = 2) | 0.7086 |
| Word Prediction (stylus, n = 2) | 0.6466 |
| Word Prediction (stylus, n = 5) | 0.5506 |
| Word Prediction (stylus, n = 10) | 0.5000 |
7.1 Performance Issues
It is reasonable to expect an inverse relation between KSPC and throughput. In other words, the greater the number of keystrokes required to produce each character, the lower the text entry throughput in words per minute. However, numerous additional factors are at work that impact performance. A few seem particularly relevant.
Repeat Keystrokes
First, the date stamp, pager, multitap, and MessagEase techniques, by their very nature, include a preponderance of keystrokes repeated on the same key, either to advance the cursor position (date stamp, pager), to advance to the next letter on the same key (multitap), or to enter frequent letters (MessagEase). This behaviour is illustrated in Table 2, showing repeat keystrokes as a ratio of all keystrokes.Not surprisingly, the ratios are quite high (> 74%) for the date stamp methods, since most keystrokes are cursor keystrokes. Auto-repeat, or typamatic, cursor strategies are clearly a desired interaction technique. Although lower for the pager (35%), multitap (47%), and MessagEase (33%), the values are significant, and should bear on performance. In key-based input the inter-key time is significantly less when successive entries are on the same key.2 This mitigates the impact of KSPC on throughput for techniques with a high percentage of repeat keystrokes.
Repeat Keystrokes as a Ratio of all Keystrokes
| Interaction Technique | Repeat Keystrokes | Interaction Technique | Repeat Keystrokes | |
|---|---|---|---|---|
| Date stamp #1 | 0.8156 | Qwerty | 0.0171 | |
| Date stamp #2 | 0.8454 | Word pred. (k, 10) | 0.0770 | |
| Date stamp #3 | 0.7858 | Word pred. (k, 5) | 0.0723 | |
| Date stamp #4 | 0.7453 | Word pred. (k, 2) | 0.0118 | |
| 5-button pager | 0.3501 | Word pred. (k, 1) | 0.0146 | |
| Multitap | 0.4684 | Word pred. (s, 1) | 0.0146 | |
| MessagEase | 0.3275 | Word pred. (s, 2) | 0.0122 | |
| LetterWise | 0.0826 | Word pred. (s, 5) | 0.0085 | |
| T9 | 0.0817 | Word pred. (s, 10) | 0.0057 |
Attention Demands
The ratio of repeat keystrokes for the other techniques in Table 2 is either very low or of questionable impact compared with other aspects of interaction. With LetterWise, T9, and word prediction, for example, there is uncertainty on the outcome of keystrokes. And so, the user must attend to the on-going process of disambiguation ("Did my keystroke produce the desired letter or word?") or prediction ("Is my intended word in the list?"). Modeling these behaviours is complex as it depends on perceptual and cognitive processes, and on user strategies. See [9] for further discussion.Visual processing times can be estimated, however. Keele and Posner [6] found that reacting to a visual stimulus (e.g., a letter or a word produced by a pressing a key), takes on the order of 190-260 ms. Interestingly, this range encompasses the "n = 1" point in the Hick-Hyman model for choice reaction time:
| RT = k × log2(n + 1) | (21) |
with k = 200 ms/bit [11, p 68]. If the user is locating a word within a ten-word list, then n = 10 and reaction time is on the order of 200 × log2(11) = 692 ms! This is additive on the keystroke time, so the impact on throughput is considerable.
Many other issues impact performance, such as errors, error correction strategies, entering punctuation symbols, etc., but space precludes further examination.
8 Conclusion
We have demonstrated the calculation of KSPC over a variety of text entry methods, with values ranging by a factor of 20, from about 10 for date stamp methods to about 0.5 for word prediction methods. Notwithstanding other factors that influence performance, it is reasonable to expect an inverse relation between KSPC and text entry throughput, measured in words per minute.
We have shown the benefit of KSPC as a tool for a priori analyses of text entry techniques. Using KSPC, potential text entry techniques can undergo analysis, comparison, and redesign prior to labour-intensive implementations and evaluations.
References
| 1. |
Bellman, T., and MacKenzie, I. S. A probabilistic character layout strategy
for mobile text entry, Proc. Graphics Interface '98. Toronto: Canadian
Information
Processing Society (1998) 168-176.
https://www.yorku.ca/mack/gi98.pdf
|
| 2. |
Card, S. K., Moran, T. P., and Newell, A.
The psychology of human-computer
interaction, Hillsdale, NJ: Lawrence Erlbaum (1983).
https://doi.org/10.1201/9780203736166
|
| 3. |
Francis, W. N., and Kucera, H.
Standard sample of present-day American English,
Providence, RI: Brown University (1964).
https://publicationsncte.org/docserver/fulltext/ce/26/4/collegeenglish24075.pdf?expires=1748525169&id=id&accname=n-109686&checksum=2CF49AB2E93641505F71079F33436848
|
| 4. |
Grinter, R. E., and Eldridge, M. A. Y do tngrs luv 2 txt msg?
Proc. ECSCW 2001.
Amsterdam: Kluwer Academic Press (2001) 219-238.
https://doi.org/10.1007/0-306-48019-0_12
|
| 5. |
Kaindl, H. Methods and modeling: Fiction or useful reality?
Extended Abstracts CHI 2001.
New York: ACM (2001) 213-214.
https://doi.org/10.1145/634067.634195
|
| 6. |
Keele, S. W., and Posner, M. I. Processing of visual feedback in rapid movements,
J. Exp. Psyc. 77
(1968) 155-158.
https://psycnet.apa.org/doi/10.1037/h0025754
|
| 7. |
MacKenzie, I. S., Kober, H., Smith, D., Jones, T., and Skepner, E. LetterWise:
Prefix-based disambiguation for mobile text input,
Proc. UIST 2001.
New York: ACM (2001) 111-120.
https://doi.org/10.1145/502348.502365
|
| 8. |
Rau, H., and Skiena, S. S. Dialing for documents: An experiment in information
theory,
Proc. UIST '94.
New York: ACM (1994) 147-155.
https://dl.acm.org/doi/pdf/10.1145/192426.192488
|
| 9. |
Silfverberg, M., MacKenzie, I. S., and Korhonen, P. Predicting text entry speed
on mobile phones,
Proc. CHI 2000.
New York: ACM (2000) 9-16.
https://doi.org/10.1145/332040.332044
|
| 10. |
Soukoreff, W., and MacKenzie, I. S. Theoretical upper and lower bounds on typing
speeds using a stylus and soft keyboard,
Behaviour & Information Technology 14
(1995) 370-379.
https://doi.org/10.1080/01449299508914656
|
| 11. |
Welford, A. T.
Fundamentals of skill,
London: Methuen, 1968.
https://gwern.net/doc/psychology/1968-welford-fundamentalsofskill.pdf
|
| 12. |
Zhai, S., Hunter, M., and Smith, B. A. The Metropolis keyboard: An exploration
of quantitative techniques for graphical keyboard design, Proc. UIST 2000.
New York: ACM (2000) 119-128.
https://dl.acm.org/doi/pdf/10.1145/354401.354424
|
-----
Notes
1. To test for a "corpus effect", all our KSPC figures were also computed using the Brown corpus [3]. The largest difference was 1.07%, with no change in the rank order of figures in Table 1. Our word-, digram-, and letter-frequency files for both corpora are available upon request.
2. Observed key repeat times are in the range of 128-176 ms [2, 9, 10, 12].