Class Throughput

java.lang.Object

Throughput

public class Throughput
extends java.lang.Object

Throughput

Summary

• Calculate Fitts' throughput for a sequence of trials
• Input data: task conditions, selection coordinates, task completion times
• Two uses:
  • As a class embedded in experiment software
  • As a utility program to process data from a terminal prompt

Background

Throughput is a commonly used dependent variable in experimental research on pointing devices or point-select techniques. However, in reviewing research papers where throughput is used, different methods of calculating throughput are found. Because of this, it is difficult to compare results between research studies. Furthermore, it is often difficult to determine with certainty how throughput was calculated. This API and Java class seek to remedy these problems by (i) providing clear and simple instructions on how to calculate throughput and (ii) disseminating a tool to do the calculations. Measures related to throughput are also calculated and described, as noted below.

This is not a primer on Fitts' law or on Fitts' throughput. For background discussions, the reader is directed to the references cited at the end of this API. Let's begin.

Fitts' throughput is calculated on a sequence of trials. The premise for this is twofold:

1. Throughput cannot be calculated on a single trial.
2. A sequence of trials is the smallest set of user actions for which throughput can be calculated as a measure of performance.

(Note: A "sequence" is consecutive series of trials for a given A-W condition.)

On the first point, the calculation of Throughput includes the variability in selection coordinates. The variability is analogous to "noise" in the information-theoretic metaphor upon which Fitts' law is based. Thus, multiple selections are required and from the coordinates of selection, the variability in the coordinates is computed.

The second point is mostly of ecological concern. After performing a single sequence of trials, the user pauses, rests, stretches, adjusts the apparatus, has a sip of tea, adjusts her position on a chair, or something. There is a demarcation between sequences and for no particular purpose other than to provide a break or pause, or perhaps to change to a different test condition. It seems reasonable that once a sequence is over, it is over! Behaviours were observed and measured and the next sequence should be treated as a separate unit of action with separate performance measurements.

Related to the second point is the following: Throughput should not be calculated on larger sets of raw data. For example, if six participants each perform five sequences of trials under the same A-W condition, there are 6 × 5 = 30 calculations of throughput, rather than a single calculation using the pooled data.

The Throughput code may be used in two ways: (i) as a class embedded in custom-designed software or (ii) as a utility program executed from a command prompt.

Throughput Class

As a class embedded in custom-designed software, the Throughput class file is placed in the same directory as other class files for the application. This API provides all the details necessary to use the Throughput class.

Use of this class begins with the instantiation of a Throughput object. The constructor receives the data necessary to characterise the sequence. The data consist of a String, two doubles, four arrays, and two integers. The arrays are all of the same size, with the size equal to the number of trials in the sequence. The data, or arguments, passed to the constructor are as follows:

Argument	Type	Description
code	String	A code to represent the conditions used for testing. This argument is used to associate test conditions (participant code, block code, device code, etc.) with the sequence. A null string may be passed if no code is necessary.
amplitude	int	Target amplitude for the sequence
width	int	Target width for the sequence
from	Point[]	The specified starting coordinates for each trial (center of the "from" target)
to	Point[]	The specified ending coordinates for each trial (center of the "to" target)
select	Point[]	The coordinates of selection where each trial was terminated
mt	int[]	The movement times (ms) for each trial
taskType	int	A constant identifying if the task movements were one-dimensional ( Throughput.ONE_DIMENSIONAL) or two-dimensional ( Throughput.TWO_DIMENSIONAL)
responseType	int	A constant identifying if the responses were serial ( Throughput.SERIAL) or discrete ( Throughput.DISCRETE). This variable is only used in calculating the effective target amplitude (see below).

The Throughput class was designed to be "universal" — as general purpose as possible. It can be used both for serial and discrete tasks and for one-dimensional (1D) or two-dimensional (2D) movement. For serial tasks, each trial immediately follows the preceding trial. For discrete tasks, each trial includes a preparatory phase followed by a stimulus. Upon detecting the stimulus, the user performs the trial. The time between the arrival of the stimulus and the beginning of movement is called reaction time and is excluded from the movement time recorded for the trial.

The one-dimensional (1D) case is the traditional back-and-forth task used by Fitts in his original 1954 paper. The two-dimensional case is the task commonly used in accordance with the ISO 9241-9 standard (updated in 2012 as ISO/TC 9241-411). For two-dimensional movements, a series of targets are arranged around a layout circle. The trials proceed in a sequence. After each selection, the next selection is the target on the opposite side of the layout circle. Every second selection is beside a target previously selected, thus the movements progress around the layout circle until all targets are selected.

Throughput is calculated for each sequence of trials as

TP = ID_e / MT

where

ID_e = log₂(A_e / W_e + 1)

and

W_e = 4.133 × SD_x

MT is the mean movement time per trial (in seconds). ID_e is the effective index of difficulty (in bits). Throughput (TP) is the rate of information processing (in bits per second).

The subscript "e" beside ID is for "effective". In the effective form, the index of difficulty reflects the task the participant actually did rather than the task the participant was presented with.

The effective target width (W_e) is calculated from SD_x, which is the standard deviation in the selection coordinates for the sequence of trials. The selection coordinates are projected onto the task axis to maintain the inherent one-dimensionality of Fitts' law. The task axis is a line between the center of the desired start point ("from") and the desired end point ("to"). The projection is done using simple calculations involving the Pythagorean identity. Details are provide below and also in the source code.

The effective target amplitude, A_e, is the mean of the actual movement amplitudes over a sequence of trials. A_e is measured along the task axis.

The following figure illustrates the geometry for a single trial, including the point of selection:

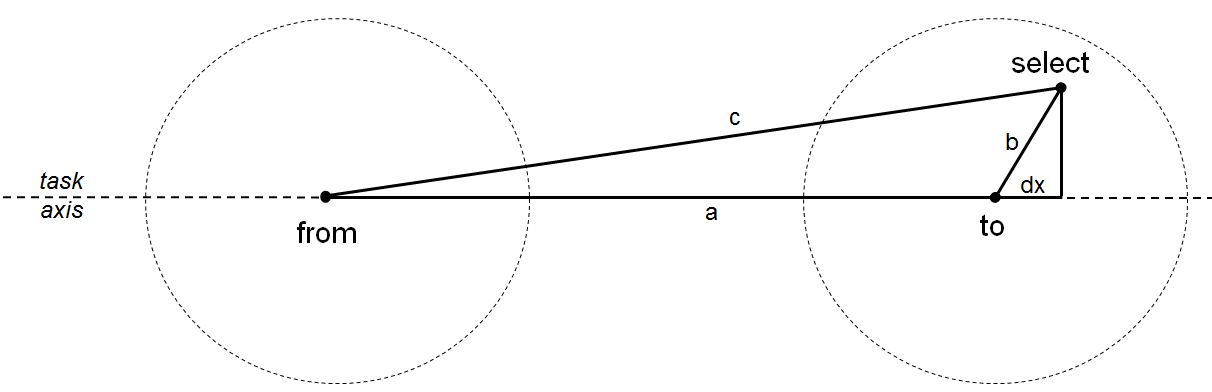
Although the figure shows a trial with horizontal movement to the right, the calculations are valid for movements in any direction or angle. Circular targets are shown to provide a conceptual visualization of the task. Other target shapes are possible, depending on the setup in the experiment. The calculation begins by computing the length of the sides connecting the from, to, and select points in the figure:

double a = Math.hypot(x1 - x2, y1 - y2);
double b = Math.hypot(x - x2, y - y2);
double c = Math.hypot(x1 - x, y1 - y);

The x-y coordinates correspond to the from (x₁, y₁), to (x₂, y₂), and select (x, y) points in the figure. Given a, b, and c, as above, dx is then calculated:

double dx = (c * c - b * b - a * a) / (2.0 * a);

Note that dx is 0 for a selection at the center of the target (as projected on the task axis), positive for a selection on the far side of the center, and negative for a selection on the near side.

The effective target amplitude is simply a + dx. For serial tasks, an additional adjustment for A _e is to add dx from the previous trial (for all trials after the first). This is necessary since each trial begins at the selection point of the previous trial. For discrete tasks, the trial is assumed to begin at the center of the "from" target.

The use of the effective target amplitude (A_e) has little influence on throughput, provided selections are distributed about the center of the targets. However, it is important to use A_e to prevent “gaming the system.” For example, if all movements fall short and only traverse, say, ¾ of A, throughput is artificially inflated if calculated using A. Using A_e prevents this. This is part of the overall premise in using “effective” values: Participants get credit for what they actually did, not for what they were asked to do.

Once a throughput object is instantiated, throughput and related measures are retrieved using public instance methods. The most relevant methods are as follows:

Method	Return Type	Description
getThroughput	double	Throughput for the sequences of trials
getAe	double	Effective target amplitude for the sequence
getWe	double	Effective target width for the sequence
getIDe	double	Effective index of difficulty for the sequence
getX	double	Mean of the x-selection coordinates for the sequence, as projected on the task axis and mapped relative to the center of the target. A return value of 0.0 corresponds to selections clustered about the center of the target, while positive or negative values correspond to selections with a mean on the near-side or far-side of the center of the target, respectively.
getSDx	double	Standard deviation in the selection coordinates, as projected on the task axis
getDeltaX	double[]	The x-selection coordinates, as projected on the task axis
getSkewness	double	Skewness in the distribution formed by the selection coordinates
getKurtosis	double	Kurtosis in the distribution formed by the selection coordinates
isNormal	boolean	The result of a test of the null hypothesis that the distribution of selection coordinates is normally distributed (p < .05). The Lilliefors test is used. If false is returned the null hypothesis is rejected, implying the distribution is not normal. If true is returned the null hypothesis is not rejected, implying the distribution has passed the test for normality.

Throughput Utility Program

NOTE: The Throughput class in GoFitts does *not* include a main method and therefore is *not* executable from a command prompt. If you wish to use the Throughput class as a utility program that is executable from a command prompt, it is available in a ZIP file along with a few other classes that are needed: Click here.

The Throughput class may be executed from a command prompt (but see NOTE above) to process data in a file. The following is the usage message if executed without arguments:

      PROMPT>java Throughput
      Usage: java Throughput datafile -t|-s
      
         where datafile = file containing data
               -t = table output
               -s = summary output (1 line per sequence)
 

The first task in using Throughput as a utility is to organize the data in a file and in the correct format. The format is simple. As an example, the data for a sequence with 20 trials are organized in 25 lines:

 
      Line     Data (comment)
      1        Code header (String – once only)
      2        Code (String – once per sequence)
      3        A, W (2 ints)
      4        Task type, Response type (2 String constants)
      5-24     From [x/y], To [x/y], Select [x/y], MT (7 ints)
      25       Blank (next sequence begins on next line)
 

Consider the file example-data.txt, which contains data formatted as above. The Throughput utility processes the data as follows (slightly abbreviated):

 
        PROMPT>java Throughput example-data.txt -t
        Code = P07,B05,G03,C03
        A = 312.0, W = 130.0 (ID = 1.77)
        Task_type = 1D, Response_type = Serial
        Data...
        ============================================================
         xFrom    yFrom     xTo      yTo     xSelect   ySelect    MT
        ------------------------------------------------------------
          540      592      227      592      218       534      262
          227      592      540      592      529       496      268
          540      592      227      592      195       608      248
          227      592      540      592      533       547      233
          540      592      227      592      209       651      251
          227      592      540      592      607       554      252
          540      592      227      592      231       650      283
          227      592      540      592      540       568      214
          540      592      227      592      231       642      301
          227      592      540      592      560       567      266
          540      592      227      592      207       653      258
          227      592      540      592      524       604      258
          540      592      227      592      239       704      248
          227      592      540      592      515       610      242
          540      592      227      592      180       675      241
          227      592      540      592      501       606      252
          540      592      227      592      215       666      243
          227      592      540      592      571       621      255
          540      592      227      592      215       690      252
          227      592      540      592      521       641      210
        ============================================================
        
        Number_of_trials = 20
        Select(x'): 9.0, -11.0, 32.0, -7.0, 18.0, 67.0, -4.0, 0.0, -4.0, 20.0, 20.0, -16.0, -12.0, -25.0, 47.0, -39.0, 12.0, 31.0, 12.0, -19.0, 
        -----
        Mean(x') = 6.55 pixels
        SD(x') = 25.57 pixels
        Skewness = 0.54
        Kurtosis = 0.37
        Is_normal? = true
        -----
        Misses = 1
        Error_rate = 5.0%
        -----
        Ae = 327.1 pixels
        We = 105.7 pixels
        IDe = 2.03 bits
        MT = 251.9 ms
        Throughput = 8.07 bps
 

The –t option is used to provide output in a tabular format (see above). The first part of the output simply echoes the input data in human readable form. After that, summary data available through the Throughput class are shown, culminating with the value of throughput (in bits per second).

As well as the values used in computing throughput, the Throughput utility provides information about the distribution of the selection coordinates, as projected on the task axis. This includes the skewness, kurtosis, and the results of a normality test. These data are useful if the research seeks to examine whether the selection coordinates form a Gaussian distribution, as assumed in the signal-and-noise model from which Fitts’ law emerged. The Is_normal? output is the result of a normality test. The null hypothesis is that the selection coordinates are normally distributed (p < .05). The Lilliefors test is used. If false is returned the null hypothesis is rejected, implying the distribution is not normal. If true is returned the null hypothesis is not rejected, implying the distribution has passed the test for normality.

The Throughput utility also outputs the number of misses in the sequence and the error rate (%). These data were not explicitly provided to the Throughput class. They are calculated based on the geometry of the trials, the task type, and the selection coordinates. The sequence of trials in the example above is from a target selection task using finger input on a touchscreen device. The outcome was TP = 8.07 bps. This value is higher than the TP typically reported for the mouse, which is generally in the 4 to 5 bps range.

The –t (table) option produces informative output; however, the organization is awkward if the analysis involves hundreds of sequences of trials, as typical in experimental research. For this, the –s (summary) option is more useful. With the –s option, the output is a rectangular, comma-delimited matrix with full-precision data. There is a header row followed by one summary row per sequence. The number of columns is n + 15, where n is the number of comma-delimited items in the code string (see the first two lines in example-data.txt). The fifteen columns following the code columns contain the summary data, excluding the raw data. The header line identifies the data in each column.

The goal with the –s option is to provide output suitable for importing into a spreadsheet or statistics application where the real work of analysing the data begins. Here's an example for the data in example-data.txt:

        PROMPT>java Throughput example-data.txt -s
        Participant,Block,Group,Condition,Task,Response,A,W,ID,N,Skewness,Kurtosis,IsNormal,Ae,We,IDe,MT,Misses,Throughput
        P07,B05,G03,C03,1D,Serial,312.000000,130.000000,1.765535,20,0.538135,0.369387,true,327.050000,105.692130,2.033640,251.850000,1,8.074805
 

Imported into a spreadsheet, the data above appear as follows (click to enlarge):

Of course, this is just a simple example. For a complete experiment, the data are likely to span hundreds, perhaps thousands, of rows. With these, the task of summarizing and analysing the data begins.

Good luck. For comments or questions, please get in touch (mack "at" yorku.ca ).

References

Fitts, P. M., The information capacity of the human motor system in controlling the amplitude of movement, Journal of Experimental Psychology, 47, 1954, 381-391. [PDF -- contact me and I'll send you the PDF]

MacKenzie, I. S., Fitts' law as a research and design tool in human-computer interaction, Human-Computer Interaction, 7, 1992, 91-139. [ PDF]

Soukoreff, R. W. and MacKenzie, I. S., Towards a standard for pointing device evaluation: Perspectives on 27 years of Fitts' law research in HCI, International Journal of Human-Computer Studies, 61, 2004, 751-789. [PDF]

MacKenzie, I. S. (2015). Fitts' throughput and the remarkable case of touch-based target selection. Proceedings of the 17th International Conference on Human-Computer Interaction - HCII 2015 (LNCS 9170), pp. 238-249. Switzerland: Springer. [ PDF]

MacKenzie, I. S. (2018). Fitts' law". In K. L. Norman & J. Kirakowski (Eds.), Handbook of human-computer interaction, pp. 349-370. Hoboken, NJ: Wiley. [PDF]

Author:

Scott MacKenzie, 2013-2024, William Soukoreff, 2013

Method Summary

Modifier and Type	Method and Description
double	getA() Returns the specified amplitude for the trials in this sequence.
double	getAe() Returns the effective amplitude for the trials in this sequence.
static double	getAe(java.awt.geom.Point2D.Double from, java.awt.geom.Point2D.Double to, java.awt.geom.Point2D.Double select) Returns the effective amplitude (Ae) for a trial.
java.lang.String	getCode() Returns the code associated with this sequence of trials.
double[]	getDeltaX() Returns the array of x-selection coordinates for this sequence of trials.
static double	getDeltaX(java.awt.geom.Point2D.Double from, java.awt.geom.Point2D.Double to, java.awt.geom.Point2D.Double select) Returns deltaX for a trial.
double	getErrorRate() Returns the error rate as a percentage.
java.awt.geom.Point2D.Double[]	getFrom() Returns a point array containing the "from" points for the trials in this sequence.
double	getID() Returns the specified index of difficulty for this sequence of trials.
double	getIDe() Returns the effective index of difficulty for this sequence of trials.
boolean	getIsNormal() Returns a boolean holding the result of a Lilliefors test for normality.
static boolean	getIsNormal(double[] d) Returns a boolean holding the result of a Lilliefors test for normality on the specified array of doubles.
double	getKurtosis() Returns the kurtosis in the selection coordinates for this sequence of trials.
static double	getKurtosis(double[] d) Returns the kurtosis in the specified array of doubles.
int	getMisses() Returns the number of misses for this sequence.
double	getMT() Returns the mean movement time (ms) for the sequence of trials.
int[]	getMTArray() Returns the double array holding the mt (movement time) values for the trials in this sequence.
int	getNumberOfTrials() Returns the number of trials in this sequence.
int	getResponseType() Returns the response type for this sequence.
java.lang.String	getResponseTypeString(int responseType) Returns a string representing the response type for this sequence.
double	getSDx() Returns the standard deviation in the selection coordinates for this sequence of trials.
java.awt.geom.Point2D.Double[]	getSelect() Returns a point array containing the "select" points for the trials in this sequence.
double	getSkewness() Returns the skewness in the selection coordinates for this sequence of trials.
static double	getSkewness(double[] d) Returns the skewness in the specified array of doubles.
int	getTaskType() Returns the task type for this sequence.
java.lang.String	getTaskTypeString(int taskType) Returns a string representing the task type for this sequence.
double	getThroughput() Returns the Throughput for the sequence of trials.
java.awt.geom.Point2D.Double[]	getTo() Returns a point array containing the "to" points for the trials in this sequence.
double	getW() Returns the specified target width for this sequence of trials.
double	getWe() Returns the effective target width for this sequence of trials.
double	getX() Returns the mean of the selection coordinates for this sequence of trials.
void	setData(java.lang.String codeArg, int amplitudeArg, int widthArg, int taskTypeArg, int responseTypeArg, java.awt.geom.Point2D.Double[] fromArg, java.awt.geom.Point2D.Double[] toArg, java.awt.geom.Point2D.Double[] selectArg, int[] mtArg) Set the data for this Throughput object.

Methods inherited from class java.lang.Object

equals, getClass, hashCode, notify, notifyAll, toString, wait, wait, wait

Method Detail

setData

public void setData(java.lang.String codeArg,
                    int amplitudeArg,
                    int widthArg,
                    int taskTypeArg,
                    int responseTypeArg,
                    java.awt.geom.Point2D.Double[] fromArg,
                    java.awt.geom.Point2D.Double[] toArg,
                    java.awt.geom.Point2D.Double[] selectArg,
                    int[] mtArg)

Set the data for this Throughput object. This method can be used to provide a new set of the data to the Throughput object (without instantiated a new object).

Parameters:

codeArg - the code

amplitudeArg - the movement amplitude

widthArg - the target width

taskTypeArg - the task type

responseTypeArg - the response type

fromArg - the from coordinate

toArg - the to coordinate

selectArg - the selection coordinate

mtArg - the movement time in milliseconds

getCode

public java.lang.String getCode()

Returns the code associated with this sequence of trials. The code is the string assigned to the sequence to associate test conditions (e.g., participant code, device code, etc.) with the sequence.

Returns:

a code for this sequence of trials

getThroughput

public double getThroughput()

Returns the Throughput for the sequence of trials.

Returns:

the throughput

getMT

public double getMT()

Returns the mean movement time (ms) for the sequence of trials.

Returns:

the movement time in millisecond

getNumberOfTrials

public int getNumberOfTrials()

Returns the number of trials in this sequence.

Returns:

the number of trials

getTaskType

public int getTaskType()

Returns the task type for this sequence. The return value is the int given to the Throughput object (via the constructor or setData). Should be Throughput.ONE_DIMENSIONAL or Throughout.TWO_DIMENSIONAL.

Returns:

the task type integer code

getTaskTypeString

public java.lang.String getTaskTypeString(int taskType)

Returns a string representing the task type for this sequence. The string returned is "1D", "2D", or "?" (if the task type is unknown).

Parameters:

taskType - a integer code for the task type

Returns:

a string for the taks type (1D or 2D)

getResponseType

public int getResponseType()

Returns the response type for this sequence. The value returned is the int constant passed to the Throughput object in the first place (via the constructor or setData). Should be Throughput.SERIAL or Throughput.DISCRETE.

Returns:

the response type integer code

getResponseTypeString

public java.lang.String getResponseTypeString(int responseType)

Returns a string representing the response type for this sequence. The string returned is "Serial", "Discrete", of "?" (if the response type is unknown).

Parameters:

responseType - a code for the response

Returns:

a string for the response type (Serial or Discrete)

getFrom

public java.awt.geom.Point2D.Double[] getFrom()

Returns a point array containing the "from" points for the trials in this sequence. The "from" points are the coordinates of the center of the target from which each trial begins.

Returns:

the from coordinate of the target

getTo

public java.awt.geom.Point2D.Double[] getTo()

Returns a point array containing the "to" points for the trials in this sequence. The "to" points are the coordinates of the center of the target to which each trial proceeds.

Returns:

the to coordinate of the target

getSelect

public java.awt.geom.Point2D.Double[] getSelect()

Returns a point array containing the "select" points for the trials in this sequence. The "select" points are the coordinates of the point of selection where each trial terminated.

Returns:

the selection coordinate

getMTArray

public int[] getMTArray()

Returns the double array holding the mt (movement time) values for the trials in this sequence.

Returns:

an array of the movement times

getSDx

public double getSDx()

Returns the standard deviation in the selection coordinates for this sequence of trials. The coordinates are projected onto the task axis.

Returns:

the standard deviation in the x coordinates

getX

public double getX()

Returns the mean of the selection coordinates for this sequence of trials. The coordinates are projected onto the task axis.

Returns:

the x coordinate

getDeltaX

public double[] getDeltaX()

Returns the array of x-selection coordinates for this sequence of trials. The coordinates are projected onto the task axis.

Returns:

the deviation from the target center

getA

public double getA()

Returns the specified amplitude for the trials in this sequence. NOTE: This value is not used in calculating Throughput. It is provided only as a convenience.

Returns:

the target amplitude

getAe

public double getAe()

Returns the effective amplitude for the trials in this sequence. The effective amplitude is the mean of the actual movement amplitudes for the sequence of trials, as projected on the task axis.

Returns:

the effective movement amplitude

getW

public double getW()

Returns the specified target width for this sequence of trials. NOTE: This value is not used in calculating Throughput. It is provided only as a convenience.

Returns:

the target width

getWe

public double getWe()

Returns the effective target width for this sequence of trials. The effective target width is 4.133 x SDx, where SDx is the standard deviation in the selection coordinates, as projected onto the task axis.

Returns:

the effective target width

getID

public double getID()

Returns the specified index of difficulty for this sequence of trials. The specified index of difficulty is ID = log2(A/W + 1). NOTE: This value is not used in calculating Throughput. It is provided only as a convenience.

Returns:

the index of difficulty

getIDe

public double getIDe()

Returns the effective index of difficulty for this sequence of trials. The effective index of difficulty, IDe = log2(Ae/We + 1).

Returns:

the effective index of difficulty

getMisses

public int getMisses()

Returns the number of misses for this sequence.

Returns:

numumber of misses

getErrorRate

public double getErrorRate()

Returns the error rate as a percentage.

Returns:

the error rate

getSkewness

public double getSkewness()

Returns the skewness in the selection coordinates for this sequence of trials. The selection coordinates are projected onto the task axis.

Returns:

the skewness

getKurtosis

public double getKurtosis()

Returns the kurtosis in the selection coordinates for this sequence of trials. The selection coordinates are projected onto the task axis.

Returns:

the kurtosis

getIsNormal

public boolean getIsNormal()

Returns a boolean holding the result of a Lilliefors test for normality. The test is done at an alpha of 0.05. The null hypothesis is that the selection coordinates in this sequence of trials, as projected on the task axis, are normally distributed. If true is returned, the null hypothesis is retained (not rejected). If false is returned, the null hypothesis is rejected.

Returns:

true if normal

getDeltaX

public static double getDeltaX(java.awt.geom.Point2D.Double from,
                               java.awt.geom.Point2D.Double to,
                               java.awt.geom.Point2D.Double select)

Returns deltaX for a trial. The geometry for a trial is defined by three points: from (center of the "from" target), to (center of the "to" target), and select (the selection coordinate). These are used in computing deltaX, which is the distance from the selection coordinate to the target center, as projected on the task axis.

NOTE: This calculation is correct, but a diagram helps to visualize the geometry. deltaX is negative for a selection on the "near side" of the target center (undershoot) and positive for a selection on the "far side" of the target center (overshoot). For a near-side selection, the a-b-c triangle is acute (i.e., a^2 + b^2 > c^2). For a far-side selection the a-b-c triangle is obtuse (i.e., a^2 + b^2 < c^2).

NOTE: This method is defined as a static method so that is may be called by an application on a per-trial basis. Recall that instances of the Throughput class work with the data for the entire sequence.

Parameters:

from - the from coordinate of the target

to - the to coordinate of the target

select - the coordinate of the selection point

Returns:

delta x (the deviation of selection from the target center)

getAe

public static double getAe(java.awt.geom.Point2D.Double from,
                           java.awt.geom.Point2D.Double to,
                           java.awt.geom.Point2D.Double select)

Returns the effective amplitude (Ae) for a trial. The geometry for a trial is defined by three points: from (center of the "from" target), to (center of the "to" target), and select (the selection coordinate). These are used in computing Ae, which is A (the distance between the "from" and "to" points) plus deltaX. See as well, getTrialDeltaX.

NOTE: The value of Ae calculated here assumes the trial started at the "from" coordinate. For serial responses, this may not be the case. An additional adjustment may be warranted for the beginning of the trial, such as adding deltaX from the previous trial (for all trials after the first trial in a sequence).

NOTE: This method is defined as a static method so that is may be called by an application on a per-trial basis. Recall that instances of the Throughput class work with the data for the entire sequence.

Parameters:

from - the from coordinate of the target

to - the to coordinate of the target

select - the coordinate of the selection point

Returns:

the effective movement amplitude

getSkewness

public static double getSkewness(double[] d)

Returns the skewness in the specified array of doubles.

Parameters:

d - the data to test

Returns:

skewness of the data in d

getKurtosis

public static double getKurtosis(double[] d)

Returns the kurtosis in the specified array of doubles.

Parameters:

d - the data to test

Returns:

kurtosis of the data in d

getIsNormal

public static boolean getIsNormal(double[] d)

Returns a boolean holding the result of a Lilliefors test for normality on the specified array of doubles. The test is done at an alpha of 0.05. The null hypothesis is that the values in the array are normally distributed. If true is returned, the null hypothesis is retained (not rejected). If false is returned, the null hypothesis is rejected.

Parameters:

d - the data to test

Returns:

true if the data in d are normally distributed