Topics

• We now cross the boundary between prehistory and history. Since, by definition, history is possible only if written documents are available, we must take a brief but important look at the nature of the documents we will be considering. A very good account is provided in How Do We Know about Greek Mathematics? Books, in the form of fairly durable codices made of flattened papyrus or vellum, do not become established as the preferred form of record until somewhere between the second and the fourth century AD. Before that, the rather perishable nature of the various media used entailed the periodical copying of texts, often by people who did not understand the material itself and who thus introduced errors, omissions and additions. It is therefore very difficult to consider such early texts as reliable records. For example (see reference above), the oldest complete copy of Euclid's Elements dates from 888 AD, when "Arethas, bishop of Caesarea Cappadociae (now in central Turkey), built up a library of religious and mathematical works." (Notice the juxtaposition of "religious" and "mathematical.") In other words, the oldest copy of this book is dated some 1200 years after the original. The same can be said of other important works from ancient Greece, for example those by Archimedes. This means that it is problematic to attribute any particular text to its original author (see How Do We Know about Greek Mathematicians?
• Let's first look at the number systems developed in ancient Greece. The first striking observation is that different number systems were developed for different uses and in different regions. This fact is not uniquely Greek—for instance, even today, several oriental languages do so. In particular, the ancient Greeks used different sets of symbols for cardinal (e.g. one, two, three,…) and ordinal numbers (e.g. first, second, third,…). "Today the number 2 is applied to any collection of two objects and 2 is thought of as an abstract property that all such collections of two objects have in common. We know that the ancient Greeks had a somewhat different idea because the numbers were used in slightly different forms depending to what the number referred. The most frequent use of this particular number system was for sums of money. The basic unit of money was the drachma with a larger unit being the talent worth 6000 drachmas. The drachma was subdivided into smaller units, namely the obol which was 1/6 of a drachma, and the chalkos which was 1/8 of an obol. Half and quarter obols were also used. Notice that this system of currency was not based on the decimal system although the number system had 10 as a base and 5 as a secondary base.." [Greek Number Systems]
  During approximately the first millenium BC, these symbols fell essentially into two groups: acrophonic (that is, "the symbols for the numerals come from the first letter of the number name"), and alphabetical or learned (the symbols for numbers followed the sequence of the letters of the alphabet—a system already used by the Phoenicians). Note also that these systems lacked zero, were not positional, and were often used for both money and weights (not unlike in some modern languages: e.g. pound. [ibidem]

   

  

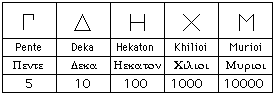
  Example of Acrophonic Numbers

   

  

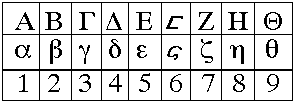
  The Alphabetical or Learned Number System

   

  It turns out that these systems made it rather cumbersome to represent very large numbers. This, of course, was not usually a problem in daily affairs, but, as I have already pointed out, even in ancient times 'mathematicians' were often interested in questions beyond daily affairs, and we know that various methods were soon proposed to overcome this problem. First Archimedes and later Apollonius basically introduced the concept of powers of ten.

   

  

  Apollonius' Representation of Large Numbers

   

  Here, for example, M^β means 10000², and χαι (which suggests και, i.e. "and") stands for "plus."
• Let us now turn to some of the applications these number systems were used for. Actually, especially early on, poetic descriptions were just as used and useful as more symbolic ones. Around 700 BC the poet Hesiod wrote a famous epic entitled Works and Days. Here are a few lines [quoted in Greek Astronomy]

  ... when the Pleiades rise it is time to use the sickle, but the plough when they are setting; 40 days they stay away from heaven; when Arcturus ascends from the sea and, rising in the evening, remain visible for the entire night, the grapes must be pruned; but when Orion and Sirius come in the middle of heaven and the rosy fingered Eos sees Arcturus, the grapes must be picked; when the Pleiades, the Hyades, and Orion are setting, then mind the plough; when the Pleiades, fleeing Orion, plunge into the dark sea, storms may be expected; 50 days after the sun's turning is the right time for man to navigate; when Orion appears, Demeter's gift has to be brought to the well-smoothed threshing floor.

  The calendar was in fact one of the earliest mathematical achievements, and underwent several changes before it could represent the rhythm of the seasons in a fairly reliable and stable fashion. Here I will make just one important observation. I said earlier that from its earliest beginning, mathematics was pursued both as a tool, and as an object of knowledge for its own sake. It is not surprising, therefore, that often results of 'pure' mathematics became confused with the results of empirical observation. Thus, for example, Pythagors—around 500 BC—"recognised that the earth was a sphere, probably more because he believed that a sphere was the most perfect shape than for genuine scientific reasons… Pythagoras had a philosophy based on mathematical 'perfection' which tended to work against a proper scientific approach. On the other side there is an important idea in the Pythagorean philosophy which had a lasting impact, namely the idea that all complex phenomena must reduce to simple ones. One should not underestimate the importance of this idea which has proved so powerful throughout the development of science, being a fundamental driving force to the great scientists such as Newton and particularly Einstein." [ibidem].
  Pythagoras' fundamental philosophical assumption was (according to Aristotle) "that things are numbers…and that the whole cosmos is a scale and a number." [quoted in Pythagoras of Samos]

  This generalisation stemmed from Pythagoras's observations in music, mathematics and astronomy. Pythagoras noticed that vibrating strings produce harmonious tones when the ratios of the lengths of the strings are whole numbers, and that these ratios could be extended to other instruments. In fact Pythagoras made remarkable contributions to the mathematical theory of music. [ibidem]

  In addition to the famous "Theorem," Pythagoras and his followers made important contributions to both pure and applied mathematics, such as the theorem that the sum of the internal angles of any triangle is 180°, and techniques for solving geometrically certain types of equations.
• Eratosthenes, believing that the Earth was round, found a way to measure its diameter. Since none of his writings has survived, the particulars of his technique can only be found in other texts.

   

  

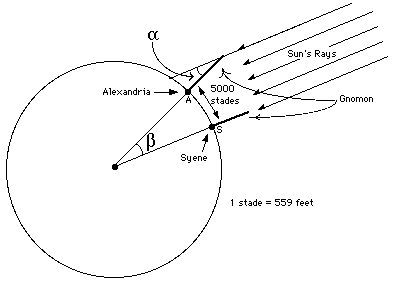
  Eratosthenes' Technique for Measuring the Diameter of the Earth

   

  How accurate is the value he found (250,000 stadia) depends on the value he adopted for the length of the stadium. Such value is not known precisely today, but Eratosthenes' result is remarkably accurate, departing no more than 10% from the modern value of the diameter of the Earth. "Eratosthenes also measured the distance to the sun as 804,000,000 stadia and the distance to the moon as 780,000 stadia. He computed these distances using data obtained during lunar eclipses. Ptolemy tells us that Eratosthenes measured the tilt of the Earth's axis with great accuracy obtaining the value of 11/83 of 180 degrees, namely 23° 51' 15"." [ibidem]
  Finally Eratosthenes invented what is now known as The Sieve of Eratosthenes, an algorithm, still in use today, for eliminating (filtering, as in through a sieve) composite numbers and thus finding prime numbers. The reference above gives a full description of the algorithm, and includes a Java applet that shows the algorithm in action. A simpler description is provided by Jill Britton; at the end of the page there is a link to an also simpler Java applet.

 
Readings, Resources and Questions

• Discuss the issues mentioned in the first bullet of this lecture, in particular the problem posed by the limited 'shelf life' of any document, including today's electronic media.
• The urge that some people have of believing that nature 'should' behave according to some a priori principle they hold is very ancient, as the case of Pythagoras demonstrates. Discuss other examples.
• Nowadays there are agreed-upon standards which define the basic units of measurements. As the case of the stadium shows, this was not always so. How can we determine the actual value of ancient units? Check for example A Brief History of Measurement.