Here I'm going to outline an exercise in Matlab that combines the following features:

1. A text file with four variants of the question
2. Random selection of the variant
3. Visual component in the form of an ASCII-art equation, like this:

    2 ⋅ s + 4 ⋅ t
a = ─────────────
        s + t       

The objective is to set up a set of individualized quiz questions that can be used in an introductory programming class, especially in a drop-in low-stakes secure testing room.

To help with extending this to allow for any number of arbitrary math problems, I've used the Diagon website as a convenient place to create variants.

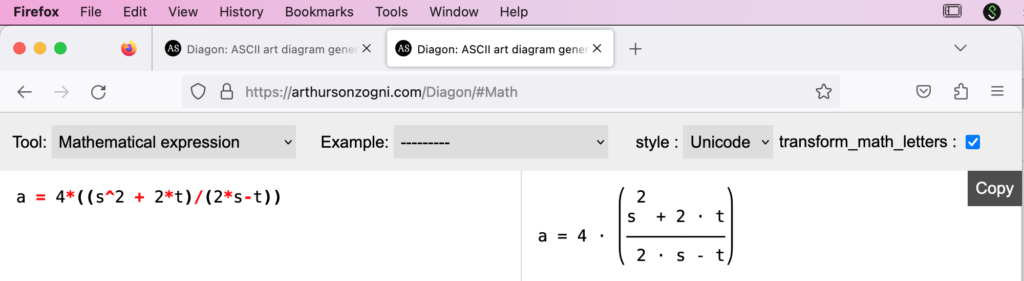
Again, the objective is to create an exercise that could be used in the context of a lab test with a locked-down computer. Students will be told ahead of time what the basic question looks like, complete with example equation, so that they can practice on their own. It will look something like this:

Dear student: write a function that implements the following equation.
There are two input variables (s and t) and one returned variable, a.
Your program should begin with the line
 
function a = studentfunction(s,t)
 
and it should end with the keyword 
 
end
 
on the last line.
 
Your function's text will be automatically graded.  You can only do this once.
So verify your answer before submitting it.
 
Here is the function that you are to implement in Matlab:
 
    2 ⋅ s + 4 ⋅ t
a = ─────────────
        s + t       

There are five files:

• diagon_scripts.txt
• diagon_equations.txt
• findspecificquestion.m
• examplequationquestion.m
• studentfunction.m

If you're thinking of doing something similar, consider renaming the files in case students attempt to figure out a way of doing a directory listing for file print from within their Matlab scripts.

Here is the first file, diagon_scripts.txt:

% first
% ----- start ----
a = (2*s + 4*t)/(s+t)
% ----- end ----
% second
% ----- start ----
a = (4*s + 2*t)/(2*s+t)
% ----- end ----
% third
% ----- start ----
a = 4*((s^2 + 2*t)/(2*s-t))
% ----- end ----
% fourth
% ----- start ----
a = 2/((s^2 + 2*t)*(2*s-t))
% ----- end ----

Each one of these equations works both inside Matlab and inside the Diagon program / website. You can use these to generate the ASCII art and Matlab can convert them from ASCII text into actual functions using the str2func() function. I used the website to generate the individual ASCII art entries, but diagon can run on both macOS and Linux machines as a command line utility, so could be integrated in a way that skips this next file. Here is the diagon_equations.txt file:

% first
% ----- start ----
    2 ⋅ s + 4 ⋅ t
a = ─────────────
        s + t       
% ----- end ----
% second
% ----- start ----
    4 ⋅ s + 2 ⋅ t
a = ─────────────
      2 ⋅ s + t  
% ----- end ----
% third
% ----- start ----
        ⎛ 2        ⎞
        ⎜s  + 2 ⋅ t⎟
a = 4 ⋅ ⎜──────────⎟
        ⎝ 2 ⋅ s - t⎠
% ----- end ----
% fourth
% ----- start ----
                 2            
a = ──────────────────────────
    ⎛ 2        ⎞              
    ⎝s  + 2 ⋅ t⎠ ⋅ (2 ⋅ s - t)
% ----- end ----

These are the entries that the student will actually see in their exercise, while the corresponding entries in the diagon_scripts.txt file are only for the auto-grader to see. In a future post, I'll do something similar but with flowcharts.

The idea is to have many variants of the target equation, so that it doesn't matter when a student does the quiz or who they've spoken to, they'll have a nearly unique experience. To extract both the reference equation and the corresponding ASCII visualization we use the following script:

function whichone = findspecificquestion(selection)
filename = 'diagon_scripts.txt';

whichone = "-1";

% selection is from 0 to 1.
if((selection>0) && (selection <=1))
    % scan the file with questions in it and determine how many we have.
    if (exist(filename, 'file') == 2)
        % File exists
        % read the file to obtain the equation
        % default to another equation if no file is present.
        fileID = fopen(filename,'r');
        firstLine = fgets(fileID);
        fclose(fileID);

        lines = readlines("diagon_scripts.txt");        % read the file into array.
        str1 = "% ----- start ----";
        str2 = "% ----- end ----";
        
        ind_log_start = strcmp(lines,str1);             % index all the starts
        index_start = find(ind_log_start);
        ind_log_end = strcmp(lines,str2);               % index all the ends
        index_end = find(ind_log_end);

        num_eqtns = length(index_start);                % how many equations?

        % find the equation desired.
        desiredvalue = lines((index_start(ceil(selection*num_eqtns)))+1);
        whichone = desiredvalue;
    else
        % File does not exist
        disp("File error.  Report this to instructor.")
        whichone = "0";
    end
else
    disp("wrong selection made.  Should be a value above zero and less than 1.")
end

This file takes an input parameter between 0 and 1 and will use that value to determine which entry in the diagon_scripts.txt file to use for the student. We have four equations here, but there could be dozens.

The Matlab file above is called from the following file, exampleequationquestion.m:

function exampleequationquestion()

DELAYTIME = 0.2;  % [seconds]

% randomize selection.
% could also do something like add up all digits in the student ID and
% choose the least significant digit of the result and divide by 10.
whichexample = rand(1);

disp("Dear student: write a function that implements the following equation.")
disp("There are two input variables (s and t) and one returned variable, a.")
disp("Your program should begin with the line")
disp(" ")
disp("function a = studentfunction(s,t)")
disp(" ")
disp("and it should end with the keyword ")
disp(" ")
disp("end")
disp(" ")
disp("on the last line.")
disp(" ")
pause(DELAYTIME);
disp("Your function's text will be automatically graded.  You can only do this once.")
disp("So verify your answer before submitting it.")
disp(" ")
disp("Here is the function that you are to implement in Matlab:")
disp(" ")

mystringequation = findspecificquestion(whichexample); % select at random.
myasciiart = findasciiart(whichexample);
disp(" ")
pause(DELAYTIME); pause(DELAYTIME); pause(DELAYTIME); pause(DELAYTIME);

disp("Pretending to wait for student to write their file...")
pause(DELAYTIME); pause(DELAYTIME); pause(DELAYTIME); pause(DELAYTIME);



disp("Generating the teacher solution...")
pause(DELAYTIME); pause(DELAYTIME); pause(DELAYTIME);pause(DELAYTIME);

% remove everything to the left of the equal sign, incluing the equal
choppedstring = extractAfter(mystringequation,"=");
choppedtext = convertStringsToChars(choppedstring);

% convert the string into a function with an input parameter, a.
teacherfunction = str2func(['@(s,t)',choppedtext]);

disp("reading the student solution...")
pause(DELAYTIME); pause(DELAYTIME); pause(DELAYTIME);pause(DELAYTIME);

disp("comparing student and teacher solutions...")


    % Test the myFunction with sample input (two random values)
    input1 = randi([0,100]);
    input2 = randi([0,100]);
    
    expectedOutput = teacherfunction(input1,input2);      % teacher's solution (reference)
    testedOutput = studentfunction(input1,input2);          % student's solution. 

    try
        assert( testedOutput == expectedOutput);          % Are teacher (expected) and student (tested) results the same?
        result = true;
    catch
        result = false;
    end
    if (result == true)
        disp([sprintf("Test succeeded. The tested function worked as tested.")]);
        disp([sprintf("Inputs %d and %d (s and t) yielded an answer of %d for an expected answer of %d", input1, input2, testedOutput,  expectedOutput)])
    else
        disp([sprintf("Test failed. The tested function did not work as tested.  ")]);
        disp([sprintf("Inputs %d and %d  (s and t)  yielded an answer of %d for an expected answer of %d", input1, input2, testedOutput,  expectedOutput)])

    end
end

We complete the files with a model student example submission, studentfunction.m:

function a = studentfunction(s,t)

a = 4*((s^2 + 2*t)/(2*s-t));

end

The actual file will have to be written by the student.

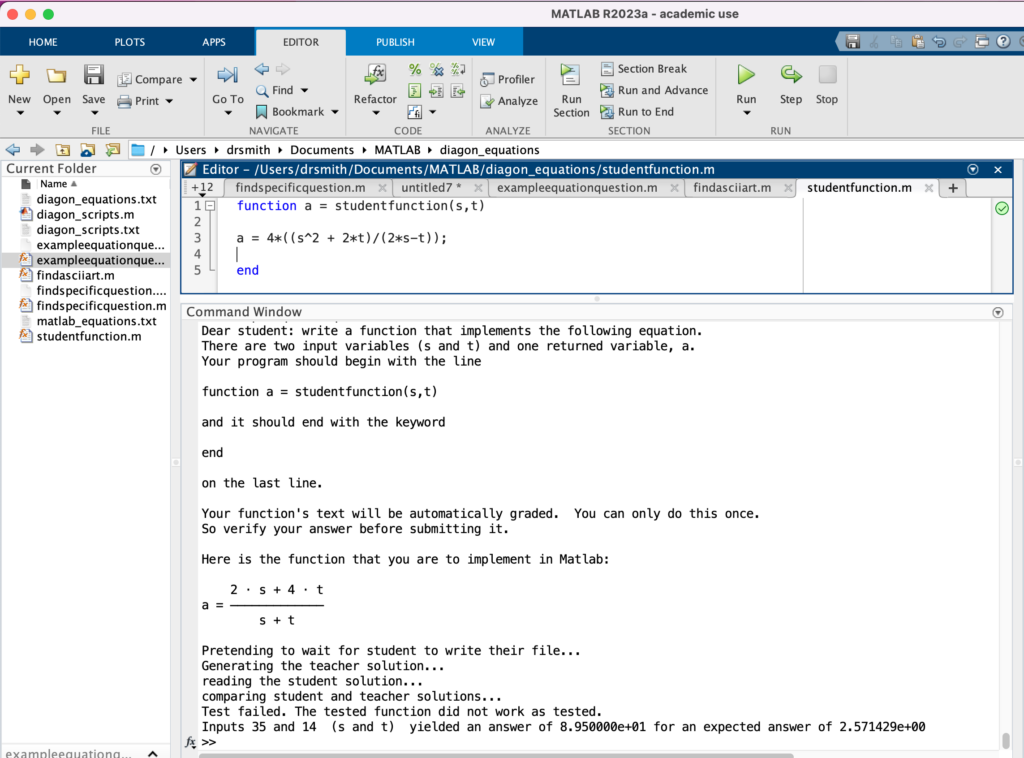
All of the files above are sufficient to run a demonstration within Matlab. They will have to be modified to work within the EECS web submit (lab test mode) or the York eClass VPL system. That work is to be done later. Here is what it looks like from the Matlab command line:

Next up, a similar approach but with flow charts!

---

James Andrew Smith is a Professional Engineer and Associate Professor in the Electrical Engineering and Computer Science Department of York University's Lassonde School, with degrees in Electrical and Mechanical Engineering from the University of Alberta and McGill University.  Previously a program director in biomedical engineering, his research background spans robotics, locomotion, human birth and engineering education. While on sabbatical in 2018-19 with his wife and kids he lived in Strasbourg, France and he taught at the INSA Strasbourg and Hochschule Karlsruhe and wrote about his personal and professional perspectives.  James is a proponent of using social media to advocate for justice, equity, diversity and inclusion as well as evidence-based applications of research in the public sphere. You can find him on Twitter. Originally from Québec City, he now lives in Toronto, Canada.