Topics

• The most famous of all the ancient Greek mathematicians are probably Euclid of Alexandria (c. 325 - 265 BC) and Archimedes of Syracuse (287 - 212 BC). While Archimedes is definitely a historical figure, and his work has reached us through a series of fairly reliable transcriptions and translations, the historical character of Euclid is much less precise, and his books are almost certainly the work of several authors, perhaps of the members of a school the gathered and flourished around Euclid, and which continued after his death. It is also rather well established that Euclid knew and made use of the work of earlier mathematicians. In any case, to realize their fundamental importance, just think that Euclid's Elements are still the basis of much of the mathematics—particularly geometry—taught in our schools, and that Archimedes discoveries can be said to have prepared the ground for the invention of calculus in the the seventeenth century.
• Each book of Euclid's Elements (there are 13 in total) opens with a series of definitions followed by a series of postulates (or axioms). These in turn are followed by the main body of the text, which is organized in terms of propositions.
  Here are the first few definitions from Book I:
  1. A point is that which has no part.
  2. A line is breadthless length.
  3. The ends of a line are points.
  4. A straight line is a line which lies evenly with the points on itself.
  5. A surface is that which has length and breadth only.
  6. The edges of a surface are lines.
  The postulates or axioms consist of statements which are considered self-evident and are thus presented without proof. Here are the five, very famous, postulates:
  1. To draw a straight line from any point to any point.
  2. To produce a finite straight line continuously in a straight line.
  3. To describe a circle with any center and radius.
  4. That all right angles equal one another.
  5. That, if a straight line falling on two straight lines makes the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
  The first three postulates are actually constructions (in modern English we would say, for example, that it is always possible to draw a straight line between two points). The fourth postulate is an implicit statement that space is homogeneous, i.e. it has the same properties everywhere. The fifth postulate is, historically, the most interesting one, since for a long time it was thought that it could be derived and proved from the other postulates. What nineteenth century mathematicians finally discovered is that, if this postulated is denied, then new, non-euclidean geometries become possible. Such geometries, far from being purely speculative, turned out to be essential to new physical theories, such as Relativity. Notice also that these constructions are in fact algorithms.
  There are in addition other postulates, called common notions, which refer to magnitudes, namely to entitties which can be compared quantitatively. Here are the five common notions:
  1. Things which equal the same thing also equal one another.
  2. If equals are added to equals, then the wholes are equal.
  3. If equals are subtracted from equals, then the remainders are equal.
  4. Things which coincide with one another equal one another.
  5. The whole is greater than the part.
  These statements, while it seems true enough that they are self-evident, appear fro the first time in Euclid's Elements. More importantly, we have since learned that, by denying one or more of them, we can enter into new realms of mathematics, which have been shown to be crucial for a deeper understanding of nature. Finally, as an example of proposition (there are 48 in Book I), here is

  Proposition 4

  If two triangles have two sides equal to two sides respectively, and have the angles contained by the equal straight lines equal, then they also have the base equal to the base, the triangle equals the triangle, and the remaining angles equal the remaining angles respectively, namely those opposite the equal sides.

  Each proposition consists of a statement (we would call it a theorem) followed by a diagram and a proof. By proof Euclid meant that the propositions could be shown to be logically deducible from the definitions and the postulates. In fact it is sufficient to show that a proposition can be deduced from a previously proved proposition.
  I will end this brief account of Euclid's work with the words of J J O'Connor and E F Robertson:

  "Euclid may not have been a first class mathematician but the long lasting nature of The Elements must make him the leading mathematics teacher of antiquity or perhaps of all time. As a final personal note let me add that my [EFR] own introduction to mathematics at school in the 1950s was from an edition of part of Euclid's Elements and the work provided a logical basis for mathematics and the concept of proof which seem to be lacking in school mathematics today."

• Let's now consider Archimedes. A quick but vivid portrait of one of the greatest mathematician and engineer is given by the historian Plutarch (c. 46 - 120 AD):

  "Archimedes possessed so high a spirit, so profound a soul, and such treasures of scientific knowledge, that though these inventions had now obtained him the renown of more than human sagacity, he yet would not deign to leave behind him any commentary or writing on such subjects; but, repudiating as sordid and ignoble the whole trade of engineering, and every sort of art that lends itself to mere use and profit, he placed his whole affection and ambition in those purer speculations where there can be no reference to the vulgar needs of life; studies, the superiority of which to all others is unquestioned, and in which the only doubt can be whether the beauty and grandeur of the subjects examined, of the precision and cogency of the methods and means of proof, most deserve our admiration…
  Oftimes Archimedes' servants got him against his will to the baths, to wash and anoint him, and yet being there, he would ever be drawing out of the geometrical figures, even in the very embers of the chimney. And while they were anointing of him with oils and sweet savours, with his fingers he drew lines upon his naked body, so far was he taken from himself, and brought into ecstasy or trance, with the delight he had in the study of geometry."

  Archimedes contributed fundamental results and computing techniques that really prepared the ground for the much later introduction of calculus and full-fledged numerical computation. He was aware that numbers such as π and most square roots were real number that could only be approximated, and invented techniques for obtaining better and better approximations.
  Here is an example of the sophisticated methods invented by Archimedes. We know that a knowledge of π is essential for calculating the circumference of a circle, and Archimedes, in his work On Spirals, proceeded first to define a spiral as follows: "If a straight line drawn in a plane revolves uniformly any number of times about a fixed extremity until it returns to its original position, and if, at the same time as the line revolves, a point moves uniformly along the straight line beginning at the fixed extremity, the point will describe a spiral in the plane."

   

  

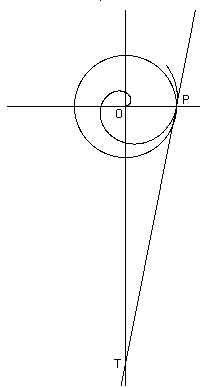
  Archimedes' Construction of the Spiral

   

  He then presents a procedure for calculating the circumference of a circle: "Let P be the point on the spiral when it has completed one turn. Let the tangent at P cut the line perpendicular to OP at T… Then OT is the length of the circumference of the circle with radius OP." This is correct, since, elsewhere, he has already demonstrated that "the area of a circle is equal to a right-angled triangle having the two shorter sides equal to the radius of the circle and the circumference of the circle. So the area of the circle with radius OP is equal to the area of the triangle OPT." [ibidem]
  Archimedes also introduced the so called Method of Exhaustion for computing the area enclosed by curved lines, for example a circle. The method consists in approximating the area (say, a circle) by a sequence of polygons (say, triangle, square, pentagon, etc.) inscribed within the area. This method is very closed related to the calculus methods introduced much later by Newton and Leibniz. Using a polygon with 96 sides inscribed in a circle, Archimedes was able to show that the value of π (= 3.1415…) lies between 3¹⁰/₇₁ (= 3.1408…) and 3¹/₇ (= 3.1428…).
  In concluding this brief review, I will mention Archimedes' important treatise The Sandreckoner, where

  "Archimedes proposes a number system capable of expressing numbers up to 8x10¹⁶ in modern notation. He argues in this work that this number is large enough to count the number of grains of sand which could be fitted into the universe. There are also important historical remarks in this work, for Archimedes has to give the dimensions of the universe to be able to count the number of grains of sand which it could contain."

  However

  "Archimedes’ estimate for the number of grains of sand sufficient to fill the then known universe, namely 10⁶³ grains of sand, is eerily similar to a well-known estimate for the total number of fundamental particles in the visible universe, namely, 2⁶⁴. These do not by any means fill our ‘universe,’ however."

 
Readings, Resources and Questions

• The military engineering works of Archimedes were better known in antiquity than his mathematical and computational works. Why?
• Archimedes is also the author of The Method. Read a nice example of the heuristic techniques used in this book.