Topics

• We will now turn to Claudius Ptolemy (c 85 - 165), the third and last major figure in our brief account of ancient Greek computational mathematics.

  "Ptolemy's Almagest shares with Euclid's Elements the glory of being the scientific text longest in use. From its conception in the second century up to the late Renaissance, this work determined astronomy as a science. During this time the Almagest was not only a work on astronomy; the subject was defined as what is described in the Almagest." [ibidem]

  It is not surprising, therefore, that several of his works have reached us, mainly through translations into Arabic, and from Arabic into Latin, although we have a Greek edition of the Almagest dating back to the ninth century, and "a very literal translation […] was made directly from the Greek by an unknown translator in Sicily" around 1160. [ see Greek Mathematics and its Modern Heirs ]
  Ptolemy' most important and best known work is the Almagest, a treatise in thirteen books. The title itself has an interesting history. It is the latinized rendition of the Arabic title Al-majisti (literally, the greatest), which is short for the Greek title The Greatest Compilation, which in turn replaced the original itile The Mathematical Compilation or The Mathematical Syntaxis. It was written around the year 150, and is an amazing compilation of mathematics and astronomy, covering the universe as it was known then. It includes observational data from the best available sources as well as from original observations by Ptolemy himself. The great merit of this work is that, under the unifying principle of the epicycles, it systematized everything that was known at the time. So well in fact that it became the astronomer's handbook for more than a millenium.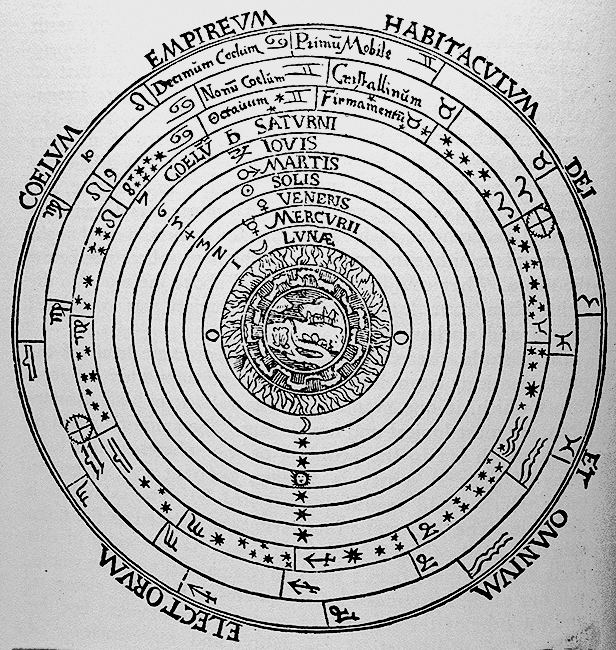

   

  

  The Ptolemaic System. From Petrus Apianus, Cosmographia (1524)

   

  Here is how Ptolemy himself outlines the purpose of the Almagest:

  "We shall try to note down everything which we think we have discovered up to the present time; we shall do this as concisely as possible and in a manner which can be followed by those who have already made some progress in the field. For the sake of completeness in our treatment we shall set out everything useful for the theory of the heavens in the proper order, but to avoid undue length we shall merely recount what has been adequately established by the ancients. However, those topics which have not been dealt with by our predecessors at all, or not as usefully as they might have been, will be discussed at length to the best of our ability.
  […]
  "[After introducing the mathematical concepts] we have to go through the motions of the sun and of the moon, and the phenomena accompanying these motions; for it would be impossible to examine the theory of the stars thoroughly without first having a grasp of these matters. Our final task in this way of approach is the theory of the stars. Here too it would be appropriate to deal first with the sphere of the so-called 'fixed stars', and follow that by treating the five 'planets', as they are called." [quoted in Claudius Ptolemy]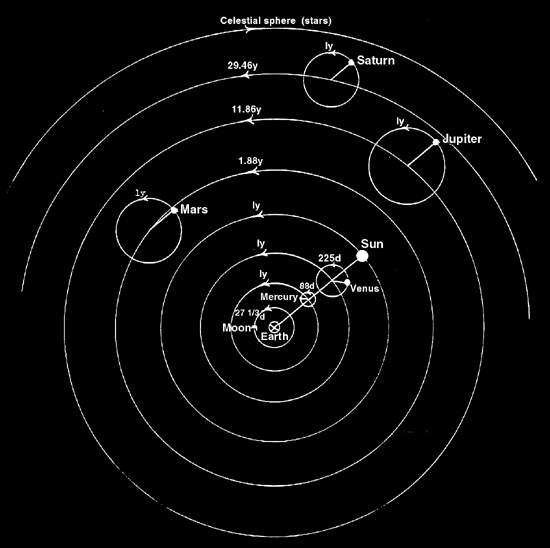

  Indeed the essential value of a theoretical framework is the amount of data it manages to describe, comprehend, explain and predict. For Ptolemy, the basic idea was the epicyle. Here are two diagrams, from Ptolemy's Planetary Models, by Robert A Hatch, University of Florida.

   

  

  A Simplified Version of the Ptolemaic Planetary Model

   

  

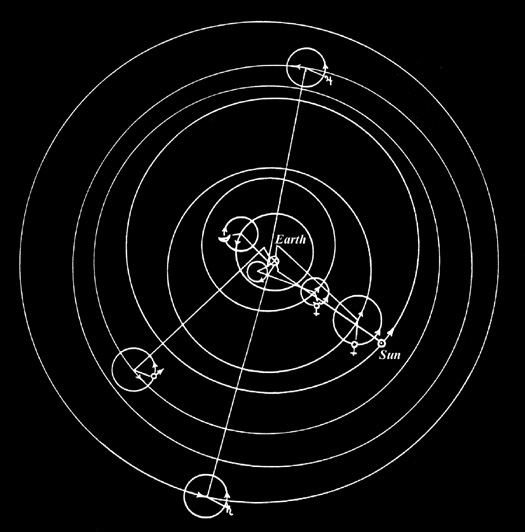
  A More Detailed Version of the Ptolemaic Planetary Model

   

  In greatly simplified words, Ptolemy's idea was that the observed motions of the planets could be accounted for by imagining the planets as moving uniformly around circles whose centers in turn moved uniformly around larger circles. The actual model is more complicated (see, for example, the second diagram above): additional circles were introduced, and sometimes the centers of these circular motions were offset in various directions and by various amounts relative to the purely geometrical centers. The fundamental assumption of course was Aristotle's "view of the world based on a fixed earth around which the sphere of the fixed stars rotates every day, carrying with it the spheres of the sun, moon, and planets." [loc. cit.] The model worked amazingly well, allowing accurate predictions of many astronomical phenomena, including eclipses.

• In order to carry out the computations involved in the description of the epicycles, Ptolemy improved upon the existing values of π. He did so by introducing the notion of chord (the straight segment connecting two points on a circle), and devising a formula for calculating its length knowing the subtending angle and the radius of the circle. The value used in the Almagest is π = 3¹⁷/₁₂₀ = 3.14166. Ptolemy discovered also many trigonometric formulas, for example those for sin(a ± b), and sin(a/2), and computed a table of the chord function in increments of ½° for the subtending angle. Tables such as these are the fruit of long, tedius work, and their usefulness was always a powerful incentive for developing new algorithms and new ways of automating the algorithms.
  The Almagest also includes one of the earliest star catalog, which lists more than a thousand stars, each one accompanied by its apparent magnitude and its celestial coordinates. See the Star Catalogue of Ptolemy.
• The Almagest was intended, in Ptolemy's words, for "those who have already made some progress in the field." In the best Greek tradition of educational works, therefore, Ptolemy wrote another book, the Planetary Hypothesis. "This work, in two books, again follows the familiar route of reducing the mathematical skills needed by a reader. Ptolemy does this rather cleverly by replacing the abstract geometrical theories by mechanical ones. [loc. cit.]
• Two other important works by Ptolemy should also be mentioned. One is Geography, where he tried to create a map of the world then known, with the latitude and longitude of the most important landmarks. Of course longitudes were very poorly known then, and continued to be so until the eighteenth century, since their measurement essentially requires a precision clock and/or a reliable star catalog. It is not surprising therefore that Ptolemy's map was greatly distorted, particularly where he describes regions far away from the much more familiar Mediterranean basin. See the online edition of the Geography prepared by Bill Thayer of the University of Kansas, or Alexander Jones' website Ptolemy and his Geography at the University of Toronto.

   

  

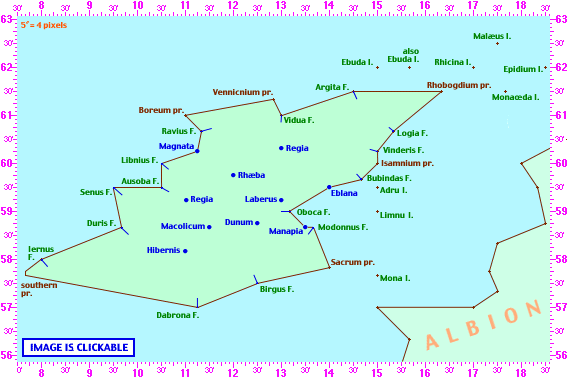
  Location of Hibernia Island of Britannia
  (Note: The image is clickable only on the original website.)

   

• The other work is the Optics or Catoptrics (this was also the title of Euclid's work in this area), where Ptolemy explores the nature of color and the laws of reflection and refraction. He does so by constructing various devices, experimenting with them, and explaining and generalizing the results in mathematical form. Although it was not until the sixteenth century that the law of reflection, and especially that of refraction, were correctly formulated, Ptolemy's results became once again the standard for the next millenium. More importantly, the deep relationship he established between experimental data and mathematical theory became a model for much further research. In this sense Ptolemy echoed Pythagoras' profound insight that "things are numbers…and that the whole cosmos is a scale and a number." [quoted in Pythagoras of Samos]

 
Readings, Resources and Questions

• In which sense can one claim to understand a phenomenon if a particular mathematical model fits the obesrvations?
• Discuss the Greek preoccupation with works that popularize science.
• Discuss Pythagoras' belief that "things are numbers…and that the whole cosmos is a scale and a number."