Topics

• "…I have sought to establish that the phenomena of nature can be reduced in the last analysis to actions at a distance between molecule and molecule, and that the consideration of these actions must serve as the basis of the mathematical theory of these phenomena."
                                                                  Pierre-Simon Laplace

• In the previous lecture I said that Newton represents the watershed between the ancient world and the modern one. By that I meant not only that he established on firm ground the "scientific method," but also that he transformed the physical sciences "into an experimentally grounded, yet analytical, quantitative, mathematical enterprise." Therefore, as mathematics developed and became more and more sophisticated, problems which would have been otherwise intractable began to elicit the interest of scientists in areas even outside the physical sciences. By and large, as illustrated by Laplace's quote above, there was the hope that the solution of such problems would parallel the exactness of the mathematical tools needed to solve them. Such hope, however, was soon to be shattered. Although they could often be formulated in precise mathematical terms, exact solutions of the mathematical equations involved turned out to be impossible: only laborious numerical approximations could be sought. One such problem is the famous three-body problem, i.e. the problem of studying the orbits of three mutually attracting bodies (e.g. the Sun, Earth and Moon) and the stability of their motion. D'Alambert, Euler, Lagrange and Laplace were among those who worked on the three-body problem. It turns out that it is not possible to find an explicit, general solution of this problem. Except in some special cases, only approximate solutions, requiring extensive calculations, can be computed. Despite some notable exceptions and the further development of computational mathematics, such realization, however, did not result in significant innovations in computational devices until the nineteenth century.
• I will focus this lecture on the new territories that applied mathematicians, and scholars in general, began exploring in this period. My purpose is to show that, once we attempt to provide formal descriptions of areas outside the physical sciences, our models become very complex, and any formal study of such models requires powerful computational tools. Although these tools were not systematically developed until the twentieth century, the eighteenth and nineteenth centuries illustrate where the need for such tools originates.
  Please refer to MacTutor's  A Mathematical Chronology.
• Already towards the end of the previous century, in 1686, the great astronomer Edmond Halley (1656 - 1742) had "published a map of the world showing the prevailing winds over the oceans. It has the distinction of being the first meteorological chart to be published." In 1693, Halley published "the mortality tables for the city of Breslau...It was one of the earliest works to relate mortality and age in a population and was highly influential in the future production of actuarial tables in life insurance." Actuarian tables, and especially weather forecasting charts, require large amounts of calculations and sophisticated algorithms, particularly when their scope extends over large areas and long periods of time.
• It is also important to pay attention to discoveries that seem at first to be only of interest to mathematicians, but are in fact motivated by or useful for the solution of practical problems. Here are a couple of examples. In 1696 Johann Bernoulli (1667 - 1748), a member of a whole family of great mathematicians, "poses the problem of the brachristochrone and challenges others to solve it. Johann Bernoulli, Jacob Bernoulli and Leibniz all solve it." The brachristochrone is a special curve defined in physical terms. Suppose a particle is constrained to move under the influence of gravity, but without friction, from point A to point B. Which curve, joining A to B, allows the particle to travel in the least time possible? This problem is part of a much larger area of mathematics, the calculus of variations, which is fundamental in applied mathematics, for example in engineering. Its origins seem to reach as far back as Newton. It was first explicitly investigated by Jacob Bernoulli (1659 - 1705). An illustration of this technique is the the study of the catenary, "the curve a hanging flexible wire or chain assumes when supported at its ends and acted upon by a uniform gravitational force," or, more practically, the curve traced by a power cable supported by two towers. Another example can be found at the end of this lecture.
• Although the first attempts to create a theory of probability go back to Pascal, Fermat and Huygens—to name just the major protagonists—in the previous century, the eighteenth century saw many systematic applications to the social sciences (as we would call them today). In 1710 John Arbuthnot (1667 - 1735) "publishes an important statistics paper in the Royal Society which discusses the slight excess of male births over female births. This paper is the first application of probability to social statistics." Although "he claims to demonstrate that divine providence, not chance, governs the sex ratio at birth," Arbuthnot's argument rests on probability theory. This type of work was soon followed, in 1710, by The Doctrine of Chances, a book by Abraham de Moivre (1667 - 1754), where, in addition to problems with dice and other games, he "investigated mortality statistics and the foundation of the theory of annuities." These works must be seen also in relation to rise of the modern insurance business. "In 1688, Lloyd's of London, named after Edward Lloyd, began the risky business of insurance underwriting."
  [ Read  History of Marine Insurance ]
  In 1764 Thomas Bayes (1702 - 1761) "publishes An Essay Towards Solving a Problem in the Doctrine of Chances […] The work contains the important Bayes' Theorem." Here is brief but good introduction to the theorem and its function from Bayes' Theorem Calculator, where you can also find a nice example and a calculator:

  Bayes' Theorem provides a way to apply quantitative reasoning to what we normally think of as "the scientific method". When several alternative hypotheses are competing for our belief, we test them by deducing consequences of each one, then conducting experimental tests to observe whether or not those consequences actually occur. If an hypothesis predicts that something should occur, and that thing does occur, it strengthens our belief in the truthfulness of the hypothesis. Conversely, an observation that contradicts the prediction would weaken (or destroy) our confidence in the hypothesis.

  In many situations, the predictions involve probabilitie—some hypothesis might predict that a certain outcome has a 30% chance of occurring, while a competing hypothesis might predict a 50% chance of the same outcome. In these situations, the occurrence or non-occurrence of the outcome would shift our relative degree of believe from one hypothesis toward another. Bayes theorem provides a way to calculate these "degree of belief" adjustments.

  In Bayes' Theorem terminology, we first construct a set of mutually-exclusive and all-inclusive hypothesis and spread our degree of belief among them by assigning a "prior probability" (number between 0 and 1) to each hypothesis. If we have no prior basis for assigning probabilities, we could just spread our "belief probability" evenly among the hypotheses.

  Then we construct a list of possible observable outcomes. This list should also be mutually exclusive and all inclusive. For each hypothesis we calculate the "conditional probability" of each possible outcome. This is just the probability of observing each outcome if that particular hypothesis is true. For each hypothesis, the sum of the conditional probabilities for all the outcomes must add up to 1.

  We then note which outcome actually occurred. Using Bayes' formula, we can then compute revised "post hoc" probabilities for the hypotheses.

  An interesting experiment, which "caused much discussion among mathematicians [and] helped towards an understanding of probability," was carried out in 1777 by Georges Louis Leclerc Comte de Buffon (1707 - 1788), who calculated π "by throwing sticks over his shoulder onto a tiled floor and counting the number of times the sticks fell across the lines between the tiles." The number so obtained (frequency) can be predicted by the theory of probability, and turns out in fact to be related to π. Notice also that Buffon was among the first to attempt to calculate the age of the earth. On the basis of his geological studies he
  • "Estimated the time it would take for a molten Earth to cool to its present state.
  • Experimented with heating irons spheres and scaling their cooling to an Earth-sized mass.
  • Got an age of 74,832 years."
  "What makes Buffon's estimate stand out is that he not only posited a physical process that required a finite time to occur (the time for the Earth to cool from a hot molten state), but performed experiments designed to help him make the best possible estimates. This is solid scientific practice."
  [ from Richard W Poggi, Introduction to Solar System Astronomy ]
  Finally, in 1785, Marie Jean Antoine Nicolas de Caritat Condorcet (1743 - 1794) "publishes Essai sur l'Application de l'Analyse à la Probabilité des Décisions Rendues à la Pluralité des Voix (Essay on the Application of the Analysis to the Probability of Majority Decisions). It is a major advance in the study of probability in the social sciences." The importance of Condorcet is summarized on MacTutor (quoting H B Acton) thus:

  "Wholly a man of the Enlightenment, an advocate of economic freedom, religious toleration, legal and educational reform, and the abolition of slavery, Condorcet sought to extend the empire of reason to social affairs. Rather than elucidate human behaviour, as had been done thus far, by recourse to either the moral or physical sciences, he sought to explain it by a merger of the two sciences that eventually became transmuted into the discipline of sociology."

• In 1711, Giovanni Ceva (1647 - 1734) "publishes De Re Nummeraria (Concerning Money Matters) which is one of the first works in mathematical economics." He "also did important work on hydraulics. On this topic he published Opus Hydrostaticum (1728). He held official positions in Mantua and used his knowledge of hydraulics to argue successfully against a project which proposed to divert the river Reno into the river Po." Hydraulics (or hydrodynamics, to use a more modern term) was a subject of great interest in this period, which saw the birth of modern engineering. For example, in 1738 Daniel Bernoulli (1700 - 1782) "publishes Hydrodynamica (Hydrodynamics). It gives for the first time the correct analysis of water flowing from a hole in a container and discusses pumps and other machines to raise water." And in 1744, "D'Alembert publishes Traité de l'Équilibre et du Mouvement des Fluides (Treatise on Equilibrium and on Movement of Fluids)." It is also important to remember that a year earlier D'Alembert had published his Traité de Dynamique (Treatise on Dynamics). "In this celebrated work he states his principle that the internal actions and reactions of a system of rigid bodies in motion are in equilibrium."
  Before concluding this lecture I wish to mention a couple of other areas of applied mathematics that were to have profound later on. In 1719, Brook Taylor (1685 - 1731) publishes New Principles of Linear Perspective. Among the many problems discussed, "there is also the interesting inverse problem which is to find the position of the eye in order to see the picture from the viewpoint that the artist intended. Taylor was not the first to discuss this inverse problem but he did make innovative contributions to the theory of such perspective problems. One could certainly consider this work as laying the foundations for the theory of descriptive and projective geometry."
  In 1733, de Moivre "first describes the normal distribution curve, or law of errors, in Approximatio ad Summam Terminorum Binomii (a+b)ⁿ in Seriem Expansi." Here is a brief introduction to the Normal Distribution Curve: Graphs, Formula, History.
  Finally, I want to touch briefly on what may first appear as a scholarly curiosity. I am referring to the problem known as the Königsberg Bridges Problem [ see, for example, Graph Theory and the Bridges of Königsberg ], which can be formulated as follows: Is it possible to design a walk which crosses each of the seven bridges exactly once? The answer was found in 1736 by the great mathematician Leonhard Euler (1707 - 1783): it is impossible!

   

  

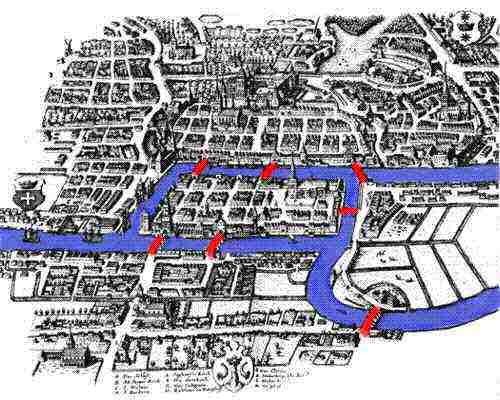
  A View of Königsberg Showing the Seven Bridges over the River Pregel

   

  The reason why this is more than a curiosity is twofold. The first is that Euler's proof represents perhaps the beginning of fundamental new chapter in mathematics: topology. To simplify quite a bit, "topology is as a 'rubber sheet geometry'—topologists study those properties of shapes that remain the same when the shapes are stretched or compressed." [ from The Beginnings of Topology…, where you can also read a simplified version of Euler's proof ]. The second reason, important in the context of this course, is that the Königsberg Bridges Problem is perhaps the simplest of a large class of problems which are very difficult, if not impossible, to solve in analytical terms. In recent times several of these problems have been solved by computers. The issue of computer proofs is a hot one, and we will return to it towards the end of the course.

 
Readings, Resources and Questions

• Referring to A Mathematical Chronology on MacTutor, examine other discoveries in this century which will lead eventually to the need for powerful computational devices.
• Try to explore why most of the mathematicians in this century focused their creative energy on mathematics and its applications, rather than on developing computational devices.
• An amusing curiosity is Mozart's Musikalisches Würfelspiel or A Musical Dice Game for Composing a Minuet.