Topics

• "To what purpose should People become fond of the Mathematicks and Natural Philosophy? … One would think at first that if the Mathematicks were to be confin'd to what is useful in them, they ought only to be improv'd in those things which have an immediate and sensible Affinity with Arts, and the rest ought to be neglected as a Vain Theory. But this would be a very wrong Notion. As for Instance, the Art of Navigation hath a necessary Connection with Astronomy, and Astronomy can never be too much improv'd for the Benefit of Navigation. Astronomy cannot be without Optics by reason of Perspective Glasses: and both, as all parts of the Mathematicks are grounded upon Geometry …"
  [ Bernard le Bouyer de Fontenelle, 1699 ]

• To get a sense of the broader historical context within which we can better understand our specific narrative, here is a brief timeline of the major historical, scientific and technological dates of the period covered in this and the next lecture, as well as in the past couple of lectures
  • Giovanni de Dondi's all-mechanical clock, with sun and planet gears (ca 1364)
  • Brunelleschi and the discovery of perspective (ca 1420)
  • Johan Gensfleisch zum Gutenberg: the first printed Bible (ca 1456)
  • Johan Froben publishes the first book with pages numbered with Arabic numerals (1516)
  • Leeuwenhoek and the invention of the microscope (ca 1590)
  • Lippershey and the invention of the telescope (ca 1608)
  • Johannes Kepler publishes the three laws of planetary motion that bear his name (1609, 1619)
  • Galileo Galilei publishes Sidereus Nuncius, where he reports on the first observations made with a telescope (1610)
  • John Napier publishes Mirifici Logarithmorum Canonis Descriptio (1614)
  • William Oughtred invents the slide-rule, an analog calculator based on logarithms (1622)
  • Pierre Vernier invents the vernier caliper (1631)
  • René Descartes published La Géométrie
  • Pascal's calculating machine (ca 1641)
  • Huygens builds the first pendulum-driven clock, accurate to a few seconds per day (1656)
  • Newton discovers a method of interpolation for computing the area under a circle (1670)
  • Leibnitz' calculating machine (ca 1671)
  • Newton publishes Philosophiae Naturalis Principia Mathematica (1687)

• The seventeenth century represent the true Renaissance of mathematics and its applications, specifically to computing. It's a period extremely rich with important figures, but we will limit our survey to the contributions which are more or less directly relevant to computing.
  We will begin with Johannes Kepler (1571 - 1630). In 1598 Kepler formulated his first attempt to develop a comprehesive cosmological theory embodying the Copernican model in his Mysterium Cosmographicum. Using the very large body of observational data collected by Tycho Brahe (1546 - 1601),

  "Kepler concluded that the orbit of Mars was an ellipse with the Sun in one of its foci (a result which when extended to all the planets is now called 'Kepler's First Law'), and that a line joining the planet to the Sun swept out equal areas in equal times as the planet described its orbit ('Kepler's Second Law'), that is the area is used as a measure of time. After this work was published in Astronomia Nova (1609), Kepler found orbits for the other planets, thus establishing that the two laws held for them too. Both laws relate the motion of the planet to the Sun; Kepler's Copernicanism was crucial to his reasoning and to his deductions [ …] The actual process of calculation for Mars was immensely laborious—there are nearly a thousand surviving folio sheets of arithmetic—and Kepler himself refers to this work as 'my war with Mars', but the result was an orbit which agrees with modern results so exactly that the comparison has to make allowance for secular changes in the orbit since Kepler's time. [ …] It was crucial to Kepler's method of checking possible orbits against observations that he have an idea of what should be accepted as adequate agreement. From this arises the first explicit use of the concept of observational error. Kepler may have owed this notion at least partly to Tycho, who made detailed checks on the performance of his instruments" [ from op. cit. ]

  Kepler himself not only made long and careful observations of the motions of the planets, and of Mars in particular, but also compiled astronomical tables which embodied both direct observations as well as data derived from these by applying his first two laws of planetary motion. This made the compilation work even more demanding in terms of calculations.

  "Kepler was accordingly delighted when in 1616 he came across Napier's work on logarithms (published in 1614). However, Maestlin promptly told him first that it was unseemly for a serious mathematician to rejoice over a mere aid to calculation and second that it was unwise to trust logarithms because no-one understood how they worked. (Similar comments were made about computers in the early 1960s.) Kepler's answer to the second objection was to publish a proof of how logarithms worked, based on an impeccably respectable source: Euclid's Elements Book 5. Kepler calculated tables of eight-figure logarithms, which were published with the Rudolphine Tables (Ulm, 1628). The astronomical tables used not only Tycho's observations, but also Kepler's first two laws. All astronomical tables that made use of new observations were accurate for the first few years after publication. What was remarkable about the Rudolphine Tables was that they proved to be accurate over decades. And as the years mounted up, the continued accuracy of the tables was, naturally, seen as an argument for the correctness of Kepler's laws, and thus for the correctness of the heliocentric astronomy. Kepler's fulfilment of his dull official task as Imperial Mathematician led to the fulfilment of his dearest wish, to help establish Copernicanism." [ from op. cit. ]

• The demands of astronomy for automating its laborious computations were answered first by the invention of the logarithms, and almost simultaneously by the invention of the first truly automated calculating machines. While logarithms were quickly adopted, the slide rule, as we saw in the previous lecture, did not quite have the success it deserved, at least in this and the subsequent century, despite the invention of the vernier caliper by Pierre Vernier (1584 - 1638), which considerably advanced the all-important process of interpolating between the readings.
  An early sort of calculating machine was the Organum Mathematicum by Gaspard Schott (1608-1666), who described and built it in 1668. It was a large box which stored ten sets of tables inscribed on corresponding cylinders, which could be mechanically turned. Each set had a specific use (see M Williams, op. cit., pp 69-92):
  • arithmetic : a standard set of Napier's bones together with addition and subtraction tables
  • geometry : tablets whose primary purpose was to solve problems encountered in survey work
  • fortification : tablets which would aid the gentlemam soldier to get the details correct when constructing the more standard types of military fortifications
  • calendar : tablets which were used in determining the date of Easter and the dates of the other major Vhristian festivals
  • gnomics : tablets which would help in the calculation of the required parameters to construct sun dials on all surfaces, independent of their direction or inclination
  • spherics : tablets which would help in the calculation of the movement of the sun, determine the times of sunrise and sunset for any given day of the year, and other similar problems
  • planetary movements : tablets to perform calculations to determine the motions of the planets and to cast horoscopes
  • earthworks : two sets of tablets dealing with the calculations involved in cut and fill problems for the construction of canals, for example
  • music : tablets which would aid the novice in composing music and creating melodies
  The context in which this 'machine' was conceived and built is, in a way, much more interesting than the machine itself, which did not work as smoothly as expected and fell into oblivion, like several similar devices. This was a time "when the Jesuit order was sending its technically trained members around the world as missionaries for both the Christian faith and the wonders of European technology." Schott, and even more so Athanasius Kircher (1602 - 1680), became the "official information exchange center to whom all foreign Jesuits communicated their latest theory, observation, or invention."
• As Michael Williams (op.cit.) points out, "almost every mechanical calculating machine has to have six basic elements in its design:
  • a set up mechanism: the device by which the number is entered into the machine…
  • a selector mechanism: the device which selects and provides the proper mechanical motion in order to cause the addition or subtraction of appropriate amounts on the regeistering mechanism
  • a registering mechanism: the device, usually a series of wheels or disks, which could be positioned to indicate the value of a number stored within the machine
  • a carry mechanism: the device which would ensure that the carry [ …] was propagated to the next digit, or even across the entire result register if necessary
  • a control mechanism: a device to ensure that all gears were properly positioned at the end of each cycle of addition to avoid inadvertently obtaining a false sum as well as jamming the machine
  • an erasing mechanism: a device which would reset the registering mechanism to store a value of zero
  The first automated, and workable, calculating machine was introduced in 1623 by Wilhelm Schickard (1592 - 1635). This machine was used by Kepler, and in fact the two of them often collaborated.

   

  

  Schickard's Calculator (Deutsches Museum, Munich)

   

  Here is a brief description that Schickard included in a letter, dated September 1623, to Kepler (from M Williams, op. cit., p. 120):

  "What you have done in a logistical way [i.e., by calculation], I have just tried to do by mechanism. I have constructed a machine consisting of eleven complete and six incomplete (actually 'mutilated') sprocket wheels which can calculate. You would burst out laughing if you were present to see how it carries by itself from one column of tens to the next or borrows from them during subtraction."

   

  

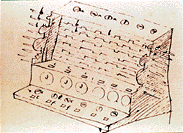
  Schickard's Sketch of the Calculator
  (Virtual Computer History Museum Group)

   

  The machine, as we said above, was used by Kepler, and it worked reliably, even though the carry mechanism was rather delicate, especially if the accumulator was designed to accept more than six digits.
• We then turn our attention to Blaise Pascal (1623 - 1662). It is quite unlikely that Pascal was aware of Schickard's Calculator, also because his machine was very different from Schickard's. Pascal's father was a tax collector, and perhaps inspired by the drudgery of the tedious calculations, in 1641 Pascal devised the first of many machines he built throughout his life. Notice that, due to the lack of precision mechanics, Pascal trained himself as one, experimenting with various materials and designs.

  "The device was contained in a box small enough to easily fit on top of a desk or small table. The upper surface of the box [ …] consisted of a number of toothed wheels above which were a series of small windows to show the results. In order to add a number, say 3, to the accumulator, it was only necessary to insert a small stylus into the toothed wheel at the position marked 3 and rotate the wheel clockwise until the stylus encountered the fixed stop, in much the same way that you would have used an old dial telephone…" [ from M Williams, op. cit., p. 126 ]

  The most important innovation was the replacement, in the carry mechanism, of the single-tooth gear with a system that exploited falling weights.

   

  

  The Pascaline (Musée des Arts et Metiers, Paris)

   

  An interesting limitation of the Pascaline was that the wheels could only turn in one direction, and thus the machine could only perform additions, not subtractions. Pascal, however, was a mathematician, and knew that subtractions are in fact no different than additions: a - b = a + (-b). The machine was rather delicate, and had to be operated quite carefully to avoid errors. Pascal tried to market it, but with no success.
• The next innovation came with a machine (ca 1671) designed by Gottfried Wilhelm von Leibniz (1646 - 1716). Leibniz knew of Pascal's invention, and early on he even tried to improve on its design, unsuccessfully, but it was only in 1672 that he demonstrated an original prototype before the Royal Society. In 1674 the final version, probably built by the French clockmaker Olivier on the basis of Leibniz' drawings and instructions, was ready.

   

  

  The Leibniz Calculating Machine (IBM)

   

  Leibniz' machine could perform multiplications by means of successive, automatic additions and shifts. According to Michael Williams (op. cit., pp 129-136), "the machine consists of two basic sections; the upper one contains the setu-up mechanism and the result register, while the lower part contains the basic Leibniz stepped-gear mechanism." The latter represents Leibniz' important and lasting contribution—so much so that the basic idea was not improved upon until the invention of the variable-toothed gear in 1875.

   

  

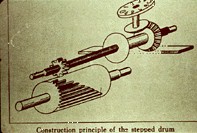
  Leibniz' Drawing of the Stepped Gear or Drum (IBM)

   

  Here is an example of how multiplication worked. (Williams, op. cit., p. 132) "…to multiply 789 by 35 the following steps were required:
  • the number to be multiplied was set up by moving the gears along the square shaft so that the pointers indicated 789
  • the crank was turned 5 times
  • the top layer of the machine was shifted one decimal place to the left
  • the crank was turned another 3 times."
  To anticipate things a little, I will note (see M Williams, op. cit., p. 135) "that the first real commercially available calculating machine was put on the market by the Frenchman Thomas de Colmar in 1820. It very closely resembles Leibniz' design…"
• The seventeenth century closes with various machines, none as innovative as the ones we discuss above, including those by Sir Samuel Morland (1625-1695) and by René Grillet (?-?). One of Morland' adding machines used a non decimal system and was suitable for use with English money, but carries had to be entered manually. See also M Williams, op. cit., pp. 136-142 and 142-145.
• We will conclude this lecture with Christiaan Huygens (1629 - 1695), who, among his many brilliant contribution to mathematics, physics and astronomy, revolutionized timekeeping with the publication of Horologium Oscillatorium Sive de Motu Pendulorum in 1673. The book 'included' (since it was full of other important mathematical results) a complete theory of pendular motion. The reason why the pendulum is such a fundamental component of the classic clock had been empirically discovered by Galileo, who around 1602 had noticed that the chandeliers suspended from the high ceilings of churches swung back and forth, in the air drafts, in such a way that the time taken by each oscillation seemed independent of the amplitude of the oscillations (the isochronism of the pendulum). Huygens showed that this is not exactly true, and that by modifying the point of suspension of the pendulum by adding cycloidal cheeks, the bob in its motion would trace a cycloid instead of a circle, and that in the oscillations would then be truly isochronic. "Huygens' early pendulum clock had an error of less than 1 minute a day, the first time such accuracy had been achieved. His later refinements reduced his clock's error to less than 10 seconds a day. [ … ] Around 1675, Huygens developed the balance wheel and spring assembly, still found in some of today's wristwatches. This improvement allowed portable 17th century watches to keep time to 10 minutes a day." [ from A Walk Through Time ]
  The development of pendulum clocks resulted also in a fundamental improvement in clock design. You will recall (see Lecture 7) that medieval clocks used the foliot balance and verge escapement system. This was now replaced by the "anchor escapement, which swung back and forth with the pendulum, its pallets alternately catching and releasing the escape wheel." [ from Pendulum Clocks ]

 
Readings, Resources and Questions

• The succession of calculating machines we have explored suggests an interesting question: in what sense does this succession demonstrate progress?
• Visit the  Huygens' Clocks exhibit at the Science Museum.